Teorema della base nella topologia indotta da una metrica

In uno spazio metrico $(X, d)$ la collezione di palle aperte $$ \mathcal{B} = \{B_d(x, \varepsilon) \mid x \in X, \varepsilon > 0\} $$ forma una base per una topologia su $X$.

Una collezione di insiemi aperti $\mathcal{B}$ è una base per una topologia se ogni insieme aperto della topologia può essere ottenuto come un'unione di insiemi della base.

Inoltre, una collezione $\mathcal{B}$ è una base se soddisfa queste due condizioni:

Per ogni punto $x \in X$, esiste almeno un insieme $B \in \mathcal{B}$ tale che $x \in B$. (Copertura)
Se $x \in B_1 \cap B_2$ per due insiemi $B_1, B_2 \in \mathcal{B}$, allora esiste un insieme $B_3 \in \mathcal{B}$ tale che $x \in B_3 \subseteq B_1 \cap B_2$. (Compatibilità delle intersezioni)

Il teorema afferma che la collezione di tutte le palle aperte $B_d(x, \varepsilon)$ soddisfa queste due condizioni e, quindi, può essere usata per definire una topologia su $X$.

Dove una palla aperta è l'insieme di tutti i punti $y \in X$ tali che la distanza tra $x$ e $y$ sia minore di $\varepsilon$ per ogni numero positivo $\varepsilon$ $$ B_d(x, \varepsilon) = \{y \in X \mid d(x, y) < \varepsilon\}. $$

In altre parole, questo teorema stabilisce che la struttura topologica di uno spazio metrico può essere descritta interamente attraverso le palle aperte.

Un esempio pratico
Dimostrazione

Un esempio pratico

Considero un insieme aperto $A$ nel piano $\mathbb{R}^2$, definito come segue:

$$ A = \{(x_1, x_2) \in \mathbb{R}^2 \mid 1 < x_1^2 + x_2^2 < 4 \} $$

Geometricamente, questo insieme rappresenta un anello nel piano, con raggio interno 1 e raggio esterno 2.

È un insieme aperto perché non include il bordo del cerchio di raggio 1 né quello di raggio 2.

esempio

Come si esprime $A$ come unione di palle aperte?

Secondo il teorema della base, posso rappresentare $A$ come un'unione di palle aperte.

Prendo per esempio alcune palle aperte centrate in punti all'interno dell'anello, ciascuna con raggio abbastanza piccolo da rimanere completamente dentro l'anello.

Ad esempio, considero la palla aperta centrata nel punto $p_1 = (1.5, 0)$ con raggio $\varepsilon_1 = 0.3$, ovvero:

$$ B1_d((1.5, 0), 0.3) = \{(x_1, x_2) \in \mathbb{R}^2 \mid d((1.5, 0), (x_1, x_2)) < 0.3\} $$

Questa palla è completamente contenuta nell'anello $A$.

esempio

Ora considero la palla aperta centrata nel punto $p_2 = (-1.5, 0)$ con raggio $\varepsilon_2 = 0.4$:

$$ B2_d((-1.5, 0), 0.4) = \{(x_1, x_2) \in \mathbb{R}^2 \mid d((-1.5, 0), (x_1, x_2)) < 0.4\} $$

Anche questa palla è contenuta interamente nell'anello $A$.

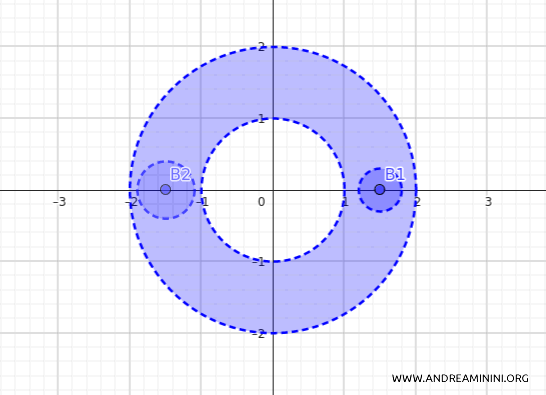
esempio

Continuando in questo modo, possiamo costruire molte altre palle aperte, centrate in diversi punti all'interno dell'anello, tutte con raggi abbastanza piccoli da rimanere interamente dentro $A$.

Il punto cruciale è che posso coprire l'intero insieme $A$ con un'unione di queste palle aperte, senza lasciare "buchi" o spazi vuoti.

Formalmente, posso scrivere:

$$ A = \bigcup_{i} B_d(x_i, \varepsilon_i) $$

Dove $x_i$ sono i centri di varie palle aperte e $\varepsilon_i$ sono i loro raggi.

Ogni $B_d(x_i, \varepsilon_i)$ è una palla aperta centrata in un punto $x_i$ con un raggio $\varepsilon_i$ tale che la palla è contenuta in $A$.

Questo esempio illustra come ogni insieme aperto (come l'anello $A$) in $\mathbb{R}^2$ possa essere rappresentato come un'unione di palle aperte.

In altre parole, le palle aperte sono le "unità fondamentali" che, combinate insieme, descrivono la struttura degli insiemi aperti in una topologia indotta da una metrica.

Dimostrazione

La dimostrazione ha l'obiettivo di dimostrare che la collezione di palle aperte in uno spazio metrico $(X, d)$ forma una base per una topologia su $X$.

Procedo verificando se le condizioni per essere una base sono soddisfatte:

1] La prima condizione afferma che ogni punto dello spazio deve appartenere a una palla aperta

In questo caso, è semplice verificarlo: per ogni punto $x \in X$, posso prendere la palla aperta $B_d(x, \varepsilon)$ con centro in $x$ e raggio $\varepsilon > 0$.

Chiaramente, il punto $x$ appartiene a $B_d(x, \varepsilon)$ per qualsiasi $\varepsilon > 0$.

Quindi, la collezione di palle aperte soddisfa la prima condizione per essere una base, poiché ogni punto di $X$ è contenuto in almeno una palla aperta.

2] La seconda condizione richiede che se un punto $x$ appartiene all'intersezione di due palle aperte $x \in B_1 \cap B_2$), allora deve esistere una palla aperta più piccola $B_3$ centrata in $x$ che è contenuta interamente nell'intersezione $B_1 \cap B_2$.

Questo è importante perché garantisce che posso "affinare" le open ball intorno a $x$ e avere sempre una copertura più piccola che rispetta la topologia.

Siano $B_1$ e $B_2$ due palle aperte in $\mathcal{B}$ (la collezione di tutte le palle aperte).

Per ipotesi suppongo che $x \in B_1 \cap B_2$. Quindi $x$ appartiene sia a $B_1$ sia a $B_2$.

Devo trovare una palla aperta $B_3$ centrata in $x$ tale che $B_3$ sia contenuta interamente in $B_1 \cap B_2$.

Se il punto $x$ appartiene a una palla aperta $B_1$, posso sempre trovare una palla aperta più piccola centrata in $x$ che è contenuta interamente in $B_1$, e la stessa cosa vale per $B_2$.

Per $B_1$, esiste una palla aperta centrata in $x$ con un certo raggio $\delta_1$ tale che $B_d(x, \delta_1) \subseteq B_1$.
Per $B_2$, esiste una palla aperta centrata in $x$ con un certo raggio $\delta_2$ tale che $B_d(x, \delta_2) \subseteq B_2$.

Ora, per ottenere una palla aperta che sia contenuta sia in $B_1$ sia in $B_2$, basta prendere la palla aperta centrata in $x$ con raggio $\delta = \min\{\delta_1, \delta_2\}$, ossia il raggio più piccolo tra i due.

Questa palla $B_d(x, \delta)$ sarà contenuta sia in $B_1$ sia in $B_2$, e quindi sarà contenuta in $B_1 \cap B_2$.

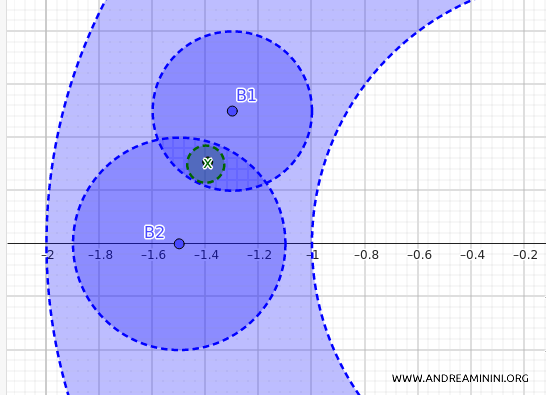
esempio

Anche la seconda condizione per essere una base è soddisfatta.

In conclusione, ho dimostrato che la collezione di palle aperte soddisfa entrambe le condizioni per essere una base.

Di conseguenza, la collezione di palle aperte forma una base per una topologia su $X$, e questa topologia è chiamata topologia indotta dalla metrica.

E così via.