L'intersezione degli interni degli insiemi
L'intersezione degli interni di due insiemi \(A\) e \(B\) è uguale all'interno dell'intersezione di quegli insiemi $ \text{Int}(A \cap B) $ $$ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) $$
L'intersezione degli interni di due insiemi \(A\) e \(B\) è uguale all'interno dell'intersezione di quegli insiemi.
In altre parole, se prendo i punti che sono all'interno di \(A\) e i punti che sono all'interno di \(B\), e poi vedo dove questi punti si sovrappongono (cioè faccio l'intersezione), ottengo esattamente i punti che sono all'interno dell'insieme \(A \cap B\).
Intuitivamente ci sono due osservazioni da fare:
- Interno di un insieme (\(\text{Int}(A)\)): Sono tutti i punti di \(A\) che non si trovano sul "bordo" dell'insieme. Ogni punto interno ha intorno a sé un piccolo cerchio che è completamente contenuto in \(A\).
- Intersezione (\(\cap\)): È l'insieme di tutti i punti che appartengono sia ad \(A\) che a \(B\).
Quindi, ovviamente, se prendo i punti dell'interno di \(A\) (\(\text{Int}(A)\)) e quelli dell'interno di \(B\) (\(\text{Int}(B)\)), e poi prendo l'intersezione di questi due insiemi di punti, ottengo esattamente l'interno dell'insieme \(A \cap B\).
Un esempio pratico
Immagino due cerchi \(A\) e \(B\) che si sovrappongono parzialmente.
L'interno di \(A\) è tutta l'area di \(A\) senza il bordo, e lo stesso vale per \(B\).
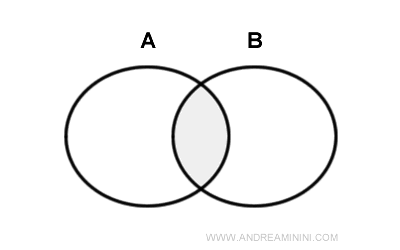
Se prendo l'intersezione di queste due aree interne, ottengo esattamente l'area interna della regione dove \(A\) e \(B\) si sovrappongono.
La dimostrazione
La dimostrazione procede in due passi:
1] Prima inclusione (\(\subseteq\))
Se un punto è interno all'insieme \(A\) ed è anche interno all'insieme \(B\), allora esiste un piccolo intorno attorno a questo punto che è completamente dentro \(A\) e anche completamente dentro \(B\).
Quindi, questo intorno è anche completamente dentro l'intersezione \(A \cap B\), il che significa che il punto è nell'interno di \(A \cap B\)
Sia \(x \in \text{Int}(A) \cap \text{Int}(B)\). Allora \(x \in \text{Int}(A)\) e \(x \in \text{Int}(B)\).
Per definizione di interno, esistono due intorni aperti \(U\) e \(V\) tali che \(x \in U \subseteq A\) e \(x \in V \subseteq B\).
Considero l'intorno \(W = U \cap V\). Poiché \(U\) e \(V\) sono aperti, anche \(W\) è aperto e contiene \(x\).
Inoltre, \(W \subseteq A \cap B\), poiché \(W \subseteq U \subseteq A\) e \(W \subseteq V \subseteq B\).
Quindi, \(x \in \text{Int}(A \cap B)\).
Ne segue che \(\text{Int}(A) \cap \text{Int}(B) \subseteq \text{Int}(A \cap B)\).
2] Seconda inclusione (\(\supseteq\))
Se un punto è nell'interno di \(A \cap B\), allora esiste un piccolo intorno attorno a questo punto che è completamente dentro \(A \cap B\).
Quindi, questo intorno è anche dentro l'insieme \(A\) e dentro l'insieme \(B\), il che significa che il punto è sia nell'interno di \(A\) che nell'interno di \(B\).
Sia \(x \in \text{Int}(A \cap B)\). Allora esiste un intorno aperto \(W\) di \(x\) tale che \(W \subseteq A \cap B\).
Poiché \(W \subseteq A \cap B\), abbiamo \(W \subseteq A\) e \(W \subseteq B\).
Quindi, \(x \in \text{Int}(A)\) e \(x \in \text{Int}(B)\).
Ne segue che \(x \in \text{Int}(A) \cap \text{Int}(B)\).
Quindi, \(\text{Int}(A \cap B) \subseteq \text{Int}(A) \cap \text{Int}(B)\).
Poiché ho dimostrato entrambe le inclusioni, posso concludere che i due insiemi sono uguali:
\[ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) \]
La dimostrazione è completa.
E così via.
