L'unione degli interni di due insiemi
L'unione degli interni di due insiemi $ A $ e $ B $ è sempre inclusa nell'interno dell'unione dei due insiemi. \[ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) \] Tuttavia, l'uguaglianza non è garantita.
Questa proprietà sottolinea che l'unione degli interni di due insiemi è sempre inclusa nell'interno della loro unione.
Tuttavia, non è garantito che questi due insiemi siano uguali. In altre parole, non è detto sempre che:
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
Potrebbe anche capitare che valga l'inclusione ma non uguaglianza.
$$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$
Questa distinzione permette di comprendere meglio le relazioni tra gli insiemi e i loro interni nel contesto della topologia.
Un esempio pratico
Considero due intervalli aperti \( A \) e \( B \) in \(\mathbb{R}\) con la topologia standard
$$ A = (0, 2) $$
$$ B = (1, 3) $$
L'interno di un intervallo aperto è l'intervallo stesso, quindi:
$$ \text{Int}(A) = (0, 2) $$
$$ \text{Int}(B) = (1, 3) $$
L'unione degli interni è:
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 2) \cup (1, 3) $$
L'unione di questi due intervalli è l'intervallo che va dal punto più piccolo al punto più grande, senza ripetizioni:
$$ (0, 2) \cup (1, 3) = (0, 3) $$
L'unione degli intervalli \( A \) e \( B \) è:
$$ A \cup B = (0, 2) \cup (1, 3) $$
Poiché gli intervalli si sovrappongono, l'unione può essere semplificata come:
$$ A \cup B = (0, 3) $$
L'interno dell'unione \( A \cup B \) è:
$$ \text{Int}(A \cup B) = \text{Int}((0, 3)) = (0, 3) $$
Ora possiamo verificare la proprietà:
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 2) \cup (1, 3) = (0, 3) $$
$$ \text{Int}(A \cup B) = \text{Int}((0, 3)) = (0, 3) $$
In questo esempio, si vede che l'unione degli interni è contenuta nell'interno dell'unione dei due insiemi.
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
Inoltre, in questo specifico caso vale anche l'uguaglianza.
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
In altri casi non è detto che si verifichi anche l'uguaglianza.
Ad esempio, se considero questi due intervalli chiusi come insiemi $$ A = [0, 2] $$ $$ B = [2, 3] $$ Gli interni dei due insiemi sono $$ \text{Int}(A) =(0,2) $$$$ \text{Int}(B) =(2,3) $$ L'interno dell'unione A∪B=[0,3] è invece l'insieme (0,3) $$ \text{Int}(A \cup B) = (0,3) $$ Quindi, continua a valere l'inclusione perché (0,2)∪(2,3) è incluso in (0,3) $$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$ Tuttavia, non vale l'uguaglianza perché il punto 2 si trova nell'interno dell'unione $$ 2 \in \text{Int}(A \cup B) = (0,3) $$ ma non si trova nell'interno Int(A), né nell'interno Int(B). $$ 2 \not \in \text{Int}(A) $$$$ 2 \not \in \text{Int}(B) $$ Quindi, il punto 2 non si trova nell'unione degli interni Int(A∪B) $$ 2 \not \in \text{Int}(A) \cup \text{Int}(B) = (0,2) \cup (2,3) $$ Pertanto, i due insiemi non sono uguali. $$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$ Questo dimostra che in generale l'unione degli interni di due insiemi è contenuta nell'interno dell'unione, ma l'uguaglianza non sempre vale.
Esempio 2
Considero ora due intervalli aperti che non si sovrappongono, ad esempio:
$$ A = (0, 1) $$
$$ B = (2, 3) $$
L'interno di ciascun intervallo è l'intervallo stesso poiché sono entrambi aperti.
$$ \text{Int}(A) = (0, 1) $$
$$ \text{Int}(B) = (2, 3) $$
L'unione degli interni è:
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 1) \cup (2, 3) $$
L'unione degli intervalli \( A \) e \( B \) è:
$$ A \cup B = (0, 1) \cup (2, 3) $$
L'interno dell'unione \( A \cup B \) è:
$$ \text{Int}(A \cup B) = \text{Int}((0, 1) \cup (2, 3)) = (0, 1) \cup (2, 3) $$
Ora posso verificare la proprietà:
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 1) \cup (2, 3) $$
$$ \text{Int}(A \cup B) = \text{Int}((0, 1) \cup (2, 3)) = (0, 1) \cup (2, 3) $$
Anche in questo caso, viene confermato che:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
In questi semplici esempi in \(\mathbb{R}\), ho dimostrato che l'unione degli interni di due intervalli è contenuta nell'interno dell'unione dei due intervalli, e in questi casi specifici, l'uguaglianza vale.
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
Tuttavia, come già detto, ci sono situazioni in spazi più complessi dove la sovrapposizione parziale può portare a un contenimento senza uguaglianza.
Esempio 3
Considero due insiemi \( A \) e \( B \) nel piano reale \(\mathbb{R}^2\) con la topologia standard.
Gli insiemi \( A \) e \( B \) sono due dischi aperti che si sovrappongono parzialmente, centrati rispettivamente in \( (0, 0) \) e \( (0.5, 0) \), entrambi con raggio \( 1 \):
$$ A = \{ (x, y) \in \mathbb{R}^2 \mid x^2 + y^2 < 1 \} $$
$$ B = \{ (x, y) \in \mathbb{R}^2 \mid (x - 0.5)^2 + y^2 < 1 \} $$
Per insiemi aperti come A e B, l'interno dell'insieme è l'insieme stesso. Quindi:
$$ \text{Int}(A)=A $$
$$ \text{Int}(B)=B $$
Quindi, l'unione degli interni è semplicemente l'unione dei due dischi:
$$ \text{Int}(A) \cup \text{Int}(B) = A \cup B $$
L'unione dei due insiemi \( A \) e \( B \) è una regione composta dai due dischi che si sovrappongono parzialmente.
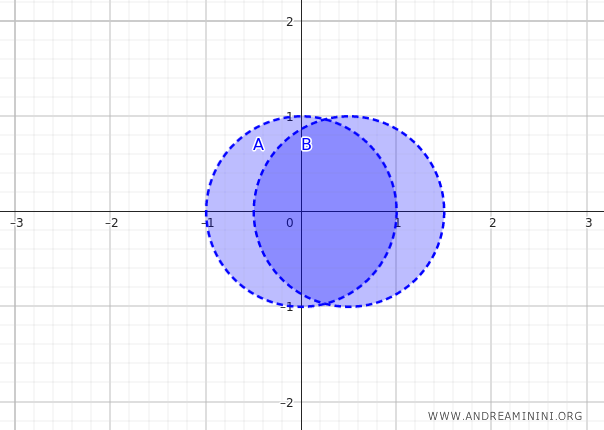
L'interno dell'unione dei due insiemi \( A \) e \( B \) contiene tutti i punti che hanno un intorno completamente contenuto in \( A \cup B \).
$$ \text{Int}(A \cup B) = A \cup B $$
Anche in questo esempio, vale l'inclusione
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
La dimostrazione
Per dimostrare la proprietà dell'unione degli interni, devo verificare che l'unione degli interni di due insiemi \( A \) e \( B \) è contenuta nell'interno dell'unione dei due insiemi.
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
Comincio la dimostrazione ricordando la definizione dell'interno di un insieme.
L'interno di un insieme \( X \), indicato come \(\text{Int}(X)\), è l'insieme di tutti i punti interni di \( X \).
Quindi, un punto \( x \) è un punto interno di \( X \) se esiste un intorno di \( x \) completamente contenuto in \( X \).
Se prendo un punto \( x \in \text{Int}(A) \cup \text{Int}(B) \), questo significa che \( x \) deve necessariamente appartenere a \(\text{Int}(A)\) oppure a \(\text{Int}(B)\).
- Se \( x \in \text{Int}(A) \), allora esiste un intorno \( U_x \) di \( x \) tale che \( U_x \subseteq A \).
- Se \( x \in \text{Int}(B) \), allora esiste un intorno \( V_x \) di \( x \) tale che \( V_x \subseteq B \).
In entrambi i casi, sia che \( x \in \text{Int}(A) \) o \( x \in \text{Int}(B) \), l'intorno \( U_x \) o \( V_x \) di \( x \) è anche contenuto in \( A \cup B \).
Questo implica che \( x \) è un punto interno di \( A \cup B \).
Pertanto, ogni punto di \(\text{Int}(A) \cup \text{Int}(B)\) è anche un punto interno di \( A \cup B \). Di conseguenza,
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
E così via.
