Le rette complanari, sghembe, parallele o incidenti nello spazio
Nello spazio due rette possono essere complanari o sghembe se condividono lo stesso piano oppure no. A loro volta, due rette complanari possono essere parallele ( distinte o coincidenti ) oppure incidenti.
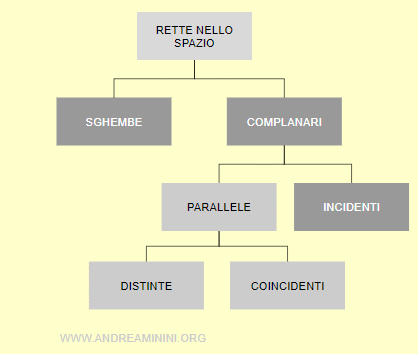
La posizione delle rette nello spazio
In uno spazio a tre dimensioni (x,y,z) due rette possono essere sghembe o complanari, a seconda della loro posizione.
- Le rette complanari
Due rette sono dette complanari se appartengono allo stesso piano. A loro volta le rette complanari sono dette rette incidenti se hanno un punto in comune, rette coincidenti se hanno tutti i punti in comune o rette parallele se non hanno alcun punto in comune.
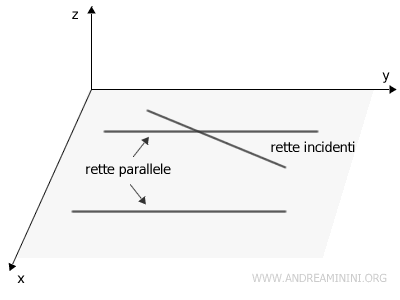
- Le rette sghembe
Due rette sono dette sghembe se non appartengono allo stesso piano nello spazio. In questo caso le due rette si trovano su piani differenti, non si intersecano e non sono parallele.
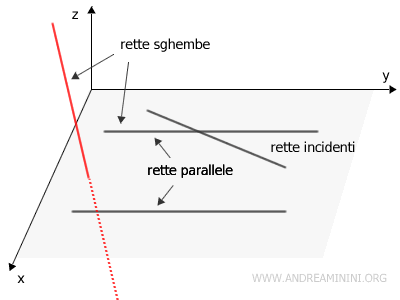
La peculiarità delle rette sghembe è che non esiste un piano unico che contenga entrambe le rette. Pertanto, le rette sghembe si distinguono dal caso dalle rette parallele, che non si intersecano ma sono nello stesso piano. Un modo per immaginare le rette sghembe è pensare a due matite tenute in aria in modo che non si tocchino e che non siano parallele.
Come verificare se due rette sono complanari
Per verificare se due rette sono complanari posso usare l'algebra lineare.
Il procedimento cambia a seconda se l'equazione della retta è in forma cartesiana o vettoriale/parametrica.
A] Equazioni cartesiane
Con le equazioni cartesiane posso rappresentare una retta anche come intersezione di piani.
$$ \begin{cases} a_1 x + b_1 y + c_1 z + d_1 = 0 \\ a_2 x + b_2 y + c_2 z + d_2 = 0 \end{cases} $$
$$ \begin{cases} a_3 x + b_3 y + c_3 z + d_3 = 0 \\ a_4 x + b_4 y + c_4 z + d_4 = 0 \end{cases} $$
Scrivo le equazioni come un sistema
$$ \begin{cases} a_1 x + b_1 y + c_1 z + d_1 = 0 \\ a_2 x + b_2 y + c_2 z + d_2 = 0 \\ a_3 x + b_3 y + c_3 z + d_3 = 0 \\ a_4 x + b_4 y + c_4 z + d_4 = 0 \end{cases} $$
ossia
$$ \begin{cases} a_1 x + b_1 y + c_1 z = - d_1 \\ a_2 x + b_2 y + c_2 z = - d_2 \\ a_3 x + b_3 y + c_3 z = - d_3 \\ a_4 x + b_4 y + c_4 z = - d_4 \end{cases} $$
Il sistema ha tre variabili (x,y,z).
La matrice dei coefficienti del sistema è
$$ A = \begin{pmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \\ a_4 & b_4 & c_4 \end{pmatrix} $$
La matrice completa del sistema è
$$ A|B = \begin{pmatrix} a_1 & b_1 & c_1 & -d_1 \\ a_2 & b_2 & c_2 & -d_2 \\ a_3 & b_3 & c_3 & -d_3 \\ a_4 & b_4 & c_4 & -d_4 \end{pmatrix} $$
Secondo il teorema di Rouché-Capelli il sistema ha soluzioni se il rango di A è uguale al rango di A|B. In questo caso le rette sono complanari incidenti o coincidenti.
- Se il rango (r) è uguale al numero delle variabili (n=3) allora il sistema ha una soluzione. Quindi le rette sono incidenti.
$$ rg(A) = rg(A|B) = 3 $$ - Se il rango (r) è inferiore al numero delle variabili (n=3) allora il sistema ha infinite soluzioni (∞n-r). Quindi le rette sono coincidenti.
$$ rg(A) = rg(A|B) < 3 $$
Se invece il rango di A è diverso dal rango di A|B allora il sistema non ha soluzioni. In questo caso le rette sono sghembe o complanari parallele.
- Se il rango (r) di A|B è uguale a 4, allora i vettori delle rette sono linearmente indipendenti. Quindi le rette sono sghembe.
$$ rg(A) \ne rg(A|B) = 4 $$ - Se il rango (r) di A|B è inferiore a 4, allora i vettori delle rette sono linearmente dipendenti. Quindi le rette sono parallele e complanari.
$$ rg(A) \ne rg(A|B) < 4 $$
Esempio
Ho le equazioni cartesiane di due rette nello spazio
$$ \begin{cases} 4x+3y+2x=4 \\ -3x+2y+z=4 \end{cases} $$
$$ \begin{cases} 3x-4y-2z=2 \\ -3x-3y+2z=1 \end{cases} $$
Le trasformo in un unico sistema lineare
$$ \begin{cases} 4x+3y+2x=4 \\ -3x+2y+z=4 \\ 3x-4y-2z=2 \\ -3x-3y+2z=1 \end{cases} $$
Poi calcolo il rango della matrice dei coefficienti A
$$ r_A \begin{pmatrix} 4 & 3 & 2 \\ -3 & 2 & 1 \\ 3 & -4 & -2 \\ -3 & -3 & 2 \end{pmatrix} = 3 $$
e il rango della matrice completa A|B
$$ r_{A|B} \begin{pmatrix} 4 & 3 & 2 & 4 \\ -3 & 2 & 1 & 4 \\ 3 & -4 & -2 & 2 \\ -3 & -3 & 2 & 1 \end{pmatrix} = 4 $$
Il rango di A non coincide con il rango di A|B.
Quindi, il sistema non ha soluzioni.
Le due rette sono sghembe perché il rango di A|B è 4.
B] Equazioni vettoriali o parametriche
Se le equazioni delle rette sono vettoriali/parametriche, devo solo verificare se i vettori direttori delle rette sono linearmente dipendenti oppure no
$$ \begin{cases} x=x_1 + l_1t_1 \\ y=y_1 + m_1t_1 \\ z=z_1 + n_1t_1 \end{cases} $$
$$ \begin{cases} x=x_2 + l_2t_2 \\ y=y_2 + m_2t_2 \\ z=z_2 + n_2t_2 \end{cases} $$
Compongo una matrice con i vettori direttori.
Poi calcolo il rango della matrice.
$$ r_k \begin{pmatrix} l_1 & l_2 \\ m_1 & m_2 \\ n_1 & n_2 \end{pmatrix} $$
Se il rango è
- rk = 1. I vettori direttori sono linearmente dipendenti. Quindi, le due rette sono parallele distinte o coincidenti. Sono comunque complanari.
- Se hanno infiniti punti in comune sono coincidenti.
- Se non hanno nessun punto in comune sono parallele.
- rk = 2. I vettori direttori sono linearmente indipendenti. In questo caso le rette potrebbero essere complanari incidenti oppure sghembe.
- Se hanno un punto in comune sono complanari incidenti.
- Se non hanno nessun punto in comune sono sghembe.
Esempio
Ho le equazioni parametriche di due rette nello spazio
$$ \begin{cases} x=3 + 2t_1 \\ y=-1 + 3t_1 \\ z=1 + 4t_1 \end{cases} $$
$$ \begin{cases} x=1 + 3t_2 \\ y=2 + t_2 \\ z=4 -2t_2 \end{cases} $$
I vettori direttori delle due rette sono
$$ v_1 = \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} $$
$$ v_2 = \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} $$
Compongo la matrice con i vettori direttori messi in colonna.
$$ \begin{pmatrix} 2 & 3 \\ 3 & 1 \\ 4 & -2 \end{pmatrix} $$
Poi calcolo il rango della matrice
$$ r_k = \begin{pmatrix} 2 & 3 \\ 3 & 1 \\ 4 & -2 \end{pmatrix} = 2 $$
Il rango è uguale a 2.
I vettori sono linearmente indipendenti.
A questo punto le rette potrebbero essere sghembe oppure complanari incidenti.
Verifico se hanno punti in comune oppure no.
$$ \begin{cases} x=3 + 2t_1 \\ y=-1 + 3t_1 \\ z=1 + 4t_1 \\ x=1 + 3t_2 \\ y=2 + t_2 \\ z=4 -2t_2 \end{cases} $$
$$ \begin{cases} 1 + 3t_2 =3 + 2t_1 \\ 2 + t_2 =-1 + 3t_1 \\ 4 -2t_2=1 + 4t_1 \end{cases} $$
$$ \begin{cases} t_2 =\frac{2 + 2t_1}{3} \\ 2 + \frac{2 + 2t_1}{3} =-1 + 3t_1 \\ 4 -2t_2=1 + 4t_1 \end{cases} $$
$$ \begin{cases} t_2 =\frac{2 + 2t_1}{3} \\ t_1 = \frac{ 11 }{7} \\ 4 -2t_2=1 + 4t_1 \end{cases} $$
$$ \begin{cases} t_2 =\frac{2 + 2(\frac{11}{7})}{3} \\ t_1 = \frac{ 11 }{7} \\ 4 -2t_2=1 + 4t_1 \end{cases} $$
$$ \begin{cases} t_2 =\frac{12}{7} \\ t_1 = \frac{ 11 }{7} \\ 4 -2 \frac{12}{7} =1 + 4 \frac{ 11 }{7} \end{cases} $$
$$ \begin{cases} t_2 =\frac{12}{7} \\ t_1 = \frac{ 11 }{7} \\ \frac{4}{7} =\frac{ 51 }{7} \end{cases} $$
Il sistema non ha soluzione. Le due rette non hanno nessun punto in comune. Non sono incidenti.
Pertanto, le due rette sono sghembe.
E così via.
