La distanza tra due rette sghembe
La distanza tra due rette sghembe $ r $ e $ s $ è la lunghezza del segmento perpendicolare $ AB $ comune che congiunge le due rette, essendo il più corto possibile tra tutti i segmenti che uniscono un punto di una retta a un punto dell'altra. $$ AB \perp r $$ $$ AB \perp s $$ Dove $ A \in r $ e $ B \in s $.
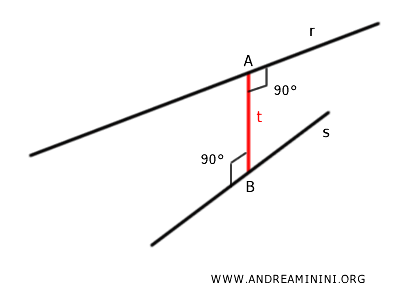
Tra due rette sghembe $ r $ e $ s $ esiste un’unica retta $ t $ perpendicolare a entrambe le rette.
Questa retta $ t $ interseca ciascuna delle due rette in un punto, $ A \in r $ e $ B \in s $, e il segmento $ AB $ che unisce questi due punti è la lunghezza minima tra i punti di una retta e i punti dell’altra.
Quindi, il segmento $ AB $ è la distanza tra le due rette sghembe $ r $ e $ s $.
Nota. Nello spazio tridimensionale (x,y,z) due rette sono sghembe se non si intersecano e non sono parallele.
La dimostrazione
Per ipotesi c'è un'unica retta perpendicolare a entrambe le rette sghembe. Questa retta interseca ciascuna delle due rette in un punto e il segmento che congiunge questi due punti è il segmento di minima distanza. Ora vediamo come dimostrarlo.
Considero due rette sghembe nello spazio tridimensonale.
Essendo sghembe, queste rette non si intersecano e non sono parallele.
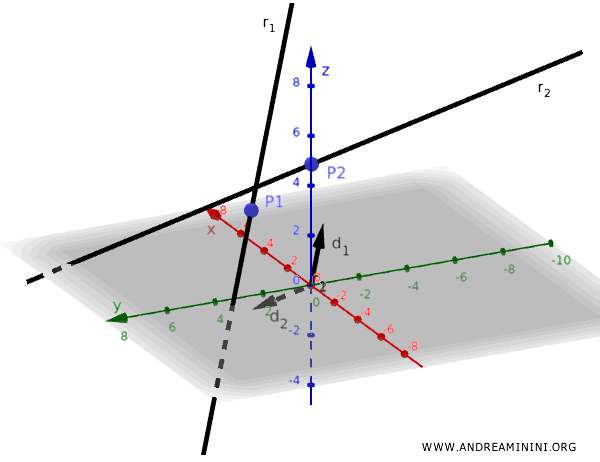
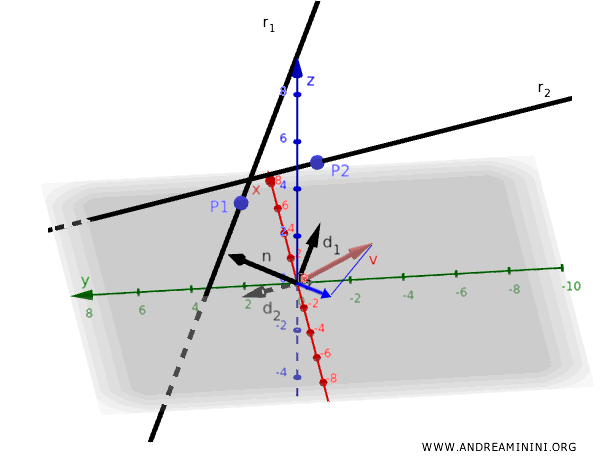
- La prima retta \( r_1 \) passa per il punto \( \mathbf{P}_1 \) e ha come direzione il vettore \( \mathbf{d}_1 \).
- La seconda retta \( r_2 \) passa per il punto \( \mathbf{P}_2 \) e ha come direzione il vettore \( \mathbf{d}_2 \).
Le equazioni parametriche delle rette sono:
$$ r_1(t) = \mathbf{P}_1 + t \, \mathbf{d}_1 \quad \text{e} \quad r_2(s) = \mathbf{P}_2 + s \, \mathbf{d}_2 $$
Dove \( t \) e \( s \) sono parametri reali.
A questo punto devo cercare una retta perpendicolare a entrambe le rette \( r_1 \) e \( r_2 \)
Una retta perpendicolare a \( r_1 \) e \( r_2 \) deve soddisfare due condizioni:
- Deve essere ortogonale al vettore direttore \( \mathbf{d}_1 \) della prima retta.
- Deve essere ortogonale al vettore direttore \( \mathbf{d}_2 \) della seconda retta.
Un vettore \( \mathbf{n} \) ortogonale a entrambi si ottiene calcolando il prodotto vettoriale:
$$ \mathbf{n} = \mathbf{d}_1 \times \mathbf{d}_2 $$
Questo \( \mathbf{n} \) è il vettore direzione della retta perpendicolare cercata.
Considero ora un vettore \( \mathbf{v} \) che va da un punto arbitrario sulla prima retta \( r_1 \) a un punto arbitrario sulla seconda retta \( r_2 \):
$$ \mathbf{v} = \mathbf{P}_2 - \mathbf{P}_1 $$
La distanza minima è data dalla proiezione di \( \mathbf{v} \) sul vettore \( \mathbf{n} \), ovvero:
$$ d = \frac{| \mathbf{v} \cdot \mathbf{n} |}{\|\mathbf{n}\|} $$
Dove \( \mathbf{v} \cdot \mathbf{n} \) è il prodotto scalare tra \( \mathbf{v} \) e \( \mathbf{n} \), \( \|\mathbf{n}\| \) è la lunghezza (norma) del vettore \( \mathbf{n} \).
La retta perpendicolare è unica perché il vettore \( \mathbf{n} \) (ottenuto come \( \mathbf{d}_1 \times \mathbf{d}_2 \)) è unico.
Quindi, anche i due punti di intersezione tra questa retta e \( r_1 \), \( r_2 \) sono univocamente determinati.
Questo garantisce che il segmento di minima distanza è unico.
Un esempio pratico
Considero due rette sghembe nello spazio con le seguenti equazioni parametriche:
La prima retta è (\( r_1 \)):
$$ r_1: \begin{cases}
x = 1 + t \\
y = 2 - t \\
z = 3 + 2t
\end{cases} $$
Dove \( \mathbf{P}_1 = (1, 2, 3) \) è un punto su \( r_1 \) e \( \mathbf{d}_1 = (1, -1, 2) \) è il suo vettore direttore.
La seconda retta (\( r_2 \)) è
$$ r_2: \begin{cases}
x = 2 + s \\
y = -1 + 2s \\
z = 4 - s
\end{cases} $$
Dove \( \mathbf{P}_2 = (2, -1, 4) \) è un punto su \( r_2 \) e \( \mathbf{d}_2 = (1, 2, -1) \) è il suo vettore direttore.
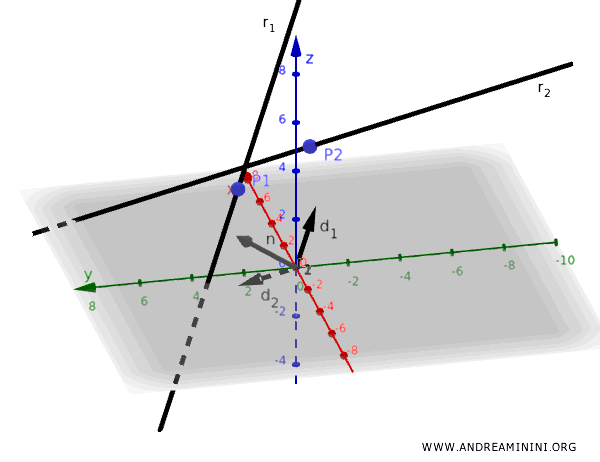
Trovo un vettore \( \mathbf{n} \) ortogonale a entrambi i vettori direttori \( \mathbf{d}_1 \) e \( \mathbf{d}_2 \) calcolando il prodotto vettoriale:
$$ \mathbf{n} = \mathbf{d}_1 \times \mathbf{d}_2 $$
Sapendo che i vettori direttori delle due rette sono \( \mathbf{d}_1 = (1, -1, 2) \) e \( \mathbf{d}_2 = (1, 2, -1) \)
$$ \mathbf{n} = \begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
1 & -1 & 2 \\
1 & 2 & -1
\end{vmatrix}
= \mathbf{i} \begin{vmatrix} -1 & 2 \\ 2 & -1 \end{vmatrix}
- \mathbf{j} \begin{vmatrix} 1 & 2 \\ 1 & -1 \end{vmatrix}
+ \mathbf{k} \begin{vmatrix} 1 & -1 \\ 1 & 2 \end{vmatrix}
$$
$$ \mathbf{n} = \mathbf{i}((-1)(-1) - (2)(2)) - \mathbf{j}((1)(-1) - (1)(2)) + \mathbf{k}((1)(2) - (1)(-1)) $$
$$ \mathbf{n} = \mathbf{i}(1 - 4) - \mathbf{j}(-1 - 2) + \mathbf{k}(2 + 1) $$
$$ \mathbf{n} = -3\mathbf{i} + 3\mathbf{j} + 3\mathbf{k} $$
Quindi, il vettore ortogonale a entrambi i vettori direttori è
$$ \mathbf{n} = (-3, 3, 3) $$
Trovo un vettore \( \mathbf{v} \) che unisce i punti \( \mathbf{P}_1 = (1, 2, 3) \) e \( \mathbf{P}_2 = (2, -1, 4) \):
$$ \mathbf{v} = \mathbf{P}_2 - \mathbf{P}_1 = (2 - 1, -1 - 2, 4 - 3) = (1, -3, 1) $$
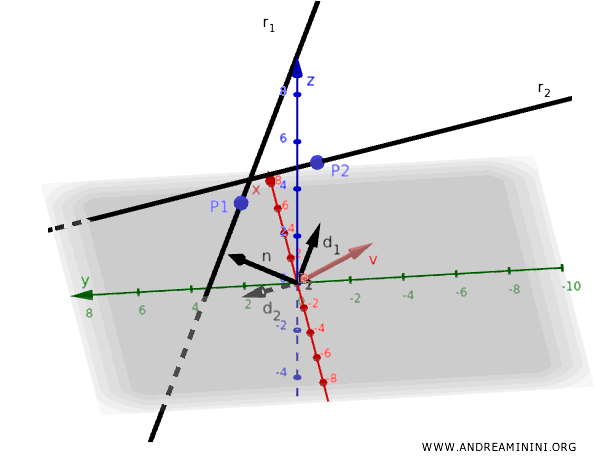
La distanza minima tra le rette è la proiezione del vettore \( \mathbf{v} \) su \( \mathbf{n} \):
Svolgo il calcolo per trovare il modulo della proiezione $ \frac{ \mathbf{v} \cdot \mathbf{n}}{||n||^2} \mathbf{n} $
$$ d = \frac{| \mathbf{v} \cdot \mathbf{n} |}{\|\mathbf{n}\|} $$
Calcolo il prodotto scalare \( \mathbf{v} \cdot \mathbf{n} \):
$$ \mathbf{v} \cdot \mathbf{n} = (1)(-3) + (-3)(3) + (1)(3) = -3 - 9 + 3 = -9 $$
Pertanto, il valore assoluto del prodotto scalare è 9
$$ | \mathbf{v} \cdot \mathbf{n} | = |-9| = 9 $$
Ora calcolo \( \|\mathbf{n}\| \), la norma di \( \mathbf{n} \):
$$ \|\mathbf{n}\| = \sqrt{(-3)^2 + 3^2 + 3^2} = \sqrt{9 + 9 + 9} = \sqrt{27} = 3\sqrt{3} $$
Quindi, la distanza è:
$$ d = \frac{9}{3\sqrt{3}} = \frac{3}{\sqrt{3}} = \sqrt{3} $$
$$ d = \sqrt{3} $$
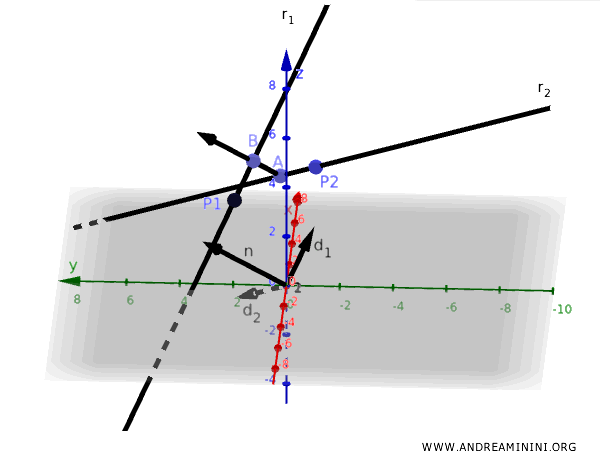
In questo caso la distanza minima tra le due rette sghembe è $ d = \sqrt{3} $
Questa è esattamente la lunghezza del segmento $ AB $ perpendicolare comune alle due rette sghembe.
E così via.
