Le proiezioni ortogonali
La proiezione ortogonale di un punto P su una retta r è il piede della perpendicolare alla retta che passa per il punto.
Ad esempio, considero un punto P e una retta r.
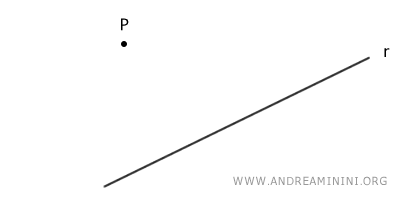
La proiezione ortogonale è l'estremo P' della perpendicolare sulla retta (piede della perpendicolare) che passa per il punto P.
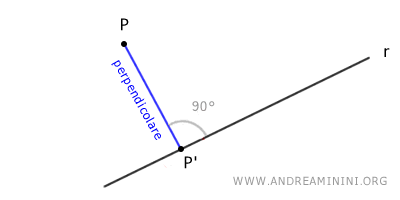
Pertanto, in questo caso la proiezione ortogonale è un punto P' della retta r.
Il segmento PP', che unisce P alla sua proiezione sulla retta r, ha lunghezza minima tra tutti i segmenti che collegano P a un punto di r.
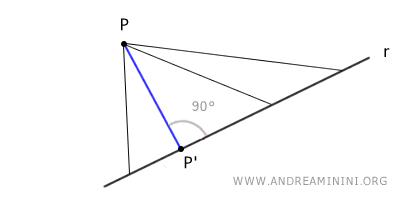
Per il punto P passa una sola retta perpendicolare a una retta datta. Quindi, è possibile tracciare una sola retta perpendicolare alla retta r che passa per il punto P.
La perpendicolare è una retta o un segmento che passa per un punto P e interseca la retta r formando un angolo retto (90°). Nel piano è il segmento più corto che ha per estremi il punto P e un punto della retta.
Dimostrazione
Per dimostrare l'esistenza e l'unicità della perpendicolare a una retta che passa per un punto P, considero due punti distinti A e B equidistanti dal piede della perpendicolare $ AP' \cong BP' $ .
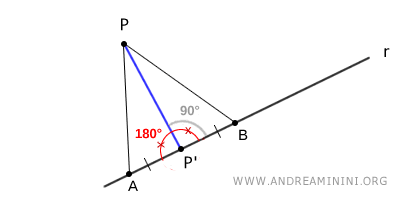
La perpendicolare forma un angolo di 90° con la retta $ r $ ed è la bisettrice dell'angolo piatto $ A\hat{P'} B = 180° $.
Poiché la bisettrice di un angolo è unica, deduco che è unica anche la perpendicolare alla retta $ r $ passante per $ P $
La proiezione di un segmento
La proiezione ortogonale di un segmento avviene in modo simile.
Ad esempio, considero un segmento AB e una retta r.
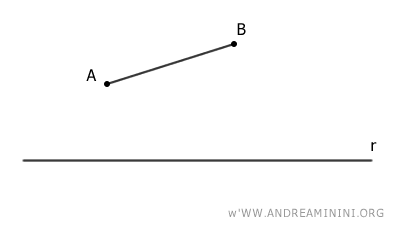
Proietto gli estremi A e B del segmento sulla retta e li unisco.
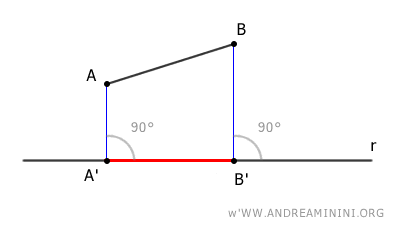
Pertanto, la proiezione ortogonale del segmento AB sulla retta r è il segmento A'B'
Nota. La proiezione ortogonale A'B' di un segmento su una retta è congruente al segmento di origine AB, solo quando quest'ultimo è parallelo alla retta.
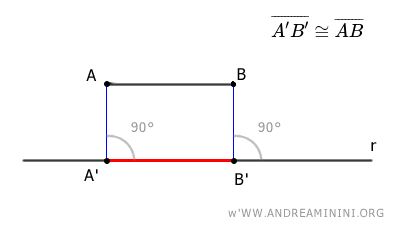
In tutti gli altri casi la lunghezza della proiezione ortogonale è sempre inferiore al segmento originale. $$ \overline{A'B'} \le \overline{AB} $$ Nel caso particolare in cui il segmento di origine è perpendicolare alla retta, la proiezione ortogonale si riduce a un solo punto.
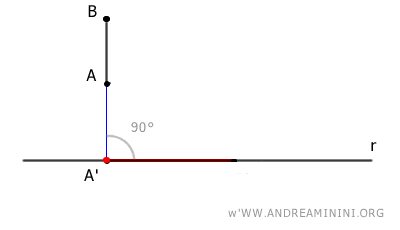
E così via.
