Il fascio improprio di rette
Un fascio improprio di rette è l'insieme di tutte le rette nel piano parallele a una data retta r.
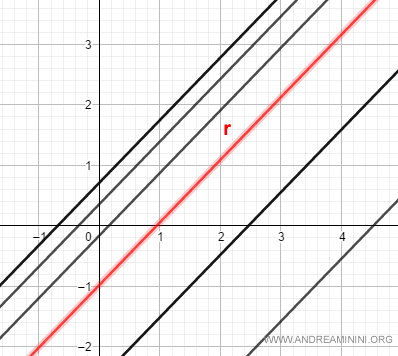
Un fascio improprio di rette è composto da infinite rette parallele.
In genere, per rappresentarlo graficamente se ne indicano soltanto una a titolo di esempio $ y = mx+q $ detta retta base del fascio di rette.
Al variare del termine noto $ q $, che è l'intercetta con l'asse y, ottengo tutte le altre rette parallele alla retta base.
$$ y = mx+q $$
In alternativa, il fascio improprio di rette posso rappresentarlo anche con l'equazione in forma implicita della retta base
$$ ax+by+k = 0 $$
In questo caso al variare di k ottengo tutte le rette parallele alla retta base.
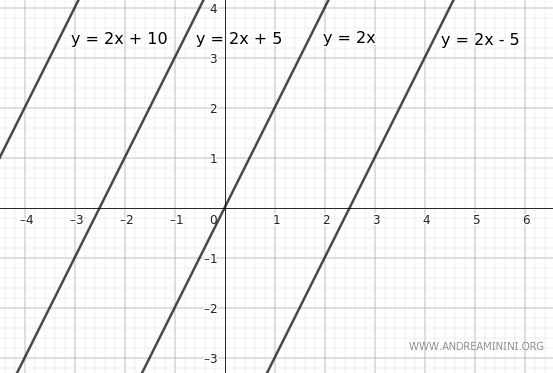
Esempio. L'equazione $ y = 2x+q $ è una retta base di un fascio di rette che comprende tutte le rette parallele che hanno m=2 come coefficiente angolare. Quando q=0 la retta passa per l'origine del piano cartesiano $ y=2x $. Per ottenere tutte le altre rette parallele mi basta assegnare dei valori al termine noto q. Ad esempio, se q=5 ottengo l'equazione della retta $ y=2x+5 $, se q=-5 ottengo la retta $ y=2x-5 $, per q=10 ho la retta $ y=2x+10 $ e via dicendo.
L'equazione in forma implicita (cartesiana) del fascio improprio di rette
L'equazione cartesiana (implicita o generale) del fascio improprio di rette è la seguente
$$ ax + by + c = 0 $$
Dove a, b sono i coefficienti della retta, sono valori costanti e diversi da zero che determinano la pendenza delle rette del fascio.
Il termine noto c, invece, è un parametro che può variare e che permette di ottenere le diverse rette all'interno dello stesso fascio.
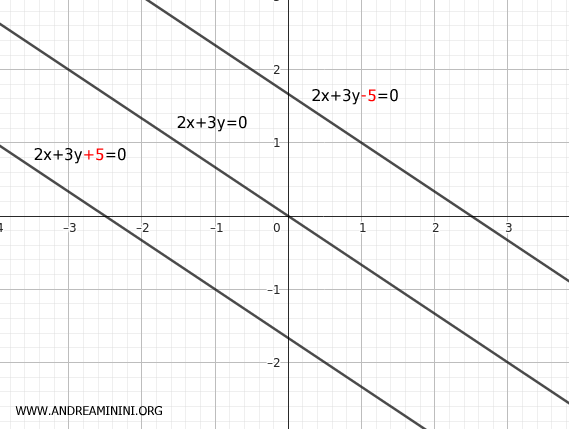
In altre parole, ogni retta del fascio improprio è caratterizzata da un valore specifico del termine noto $ c $ che determina la posizione e la distanza della retta rispetto alle altre rette parallele.
Nel caso particolare in cui il termine noto è nullo (c=0) la retta passa per l'origine del piano cartesiano ossia nel punto alle coordinate (x;y)=(0;0).
Nota. Anche la retta principale r, quella "base" a cui tutte le altre rette sono parallele, ha un valore specifico e unico del termine noto c . Ad esempio, se considero come retta base del fascio di rette l'equazione $ 2x+3y-5=0 $ il termine noto è $ c=-5 $.
Ci sono due casi particolari che è utile menzionare:
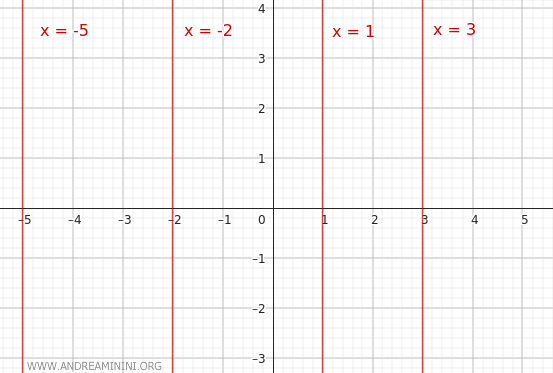
- $ x=k $
Questa è l'equazione di un fascio improprio di rette parallele all'asse y. In questa configurazione, ogni retta del fascio ha una diversa intercetta sull'asse x determinata dal valore di k, ma nessuna pendenza rispetto all'asse y. Quindi, risultano rette verticali. Nel caso particolare x=0 la retta corrisponde all'asse delle ordinate. Ad esempio, x=-5, x=-2, x=1, x=3, ecc.
- $ y=k $
Questa equazione rappresenta un fascio improprio di rette parallele all'asse x. Ogni retta ha una diversa intercetta sull'asse y, a seconda del valore di k), e sono rette orizzontali senza pendenza rispetto all'asse x. Nel caso particolare in cui y=0 la retta coincide con l'asse delle ascisse. Altri esempi sono y=3, y=1, y=-1, y=-2, ecc.
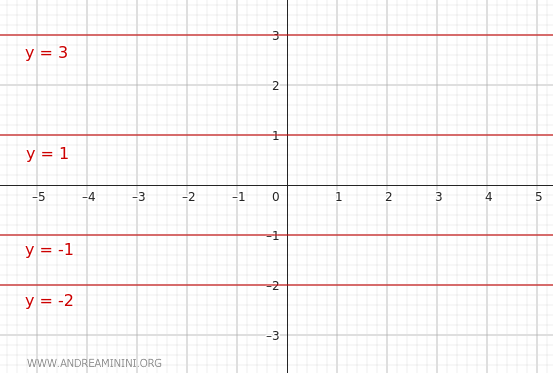
Questi due casi speciali sono utili per descrivere insiemi di rette che mantengono una direzione fissa mentre si spostano parallelamente lungo l'altro asse.
L'equazione del fascio di rette in forma esplicita
In alternativa, l'equazione del fascio improprio di rette può anche essere espressa in forma esplicita come:
$$ y = mx + q $$
In questo caso ogni retta del fascio ha un valore unico di q.
Se q=0, la retta interseca l'origine.
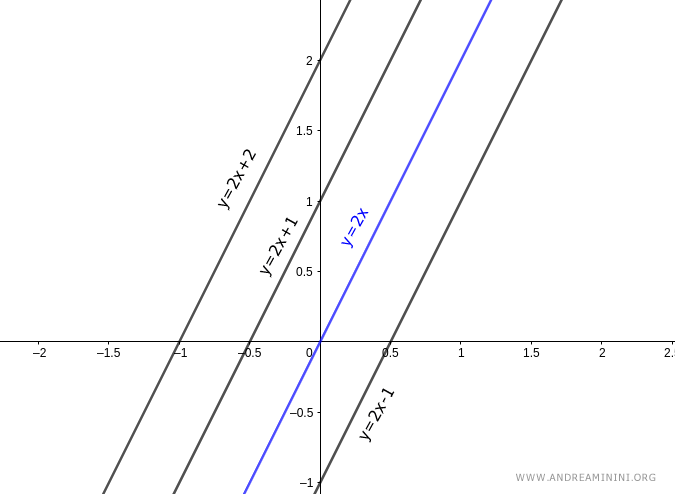
Nota. Il termine q è il termine noto dell'equazione e rappresenta l'intercetta sull'asse y in corrispondenza del valore x=0.
L'equazione parametrica
Un'altra rappresentazione è data dall'equazione parametrica
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + t \cdot \begin{pmatrix} l \\ m \end{pmatrix} $$
Dove la combinazione (x0,y0) varia per ogni retta nel fascio, mentre il vettore direttore (l,m) rimane costante.
Esempio
Data la retta:
$$ 2x +3y - 12 = 0 $$
Variando c si generano rette parallele nel fascio improprio.
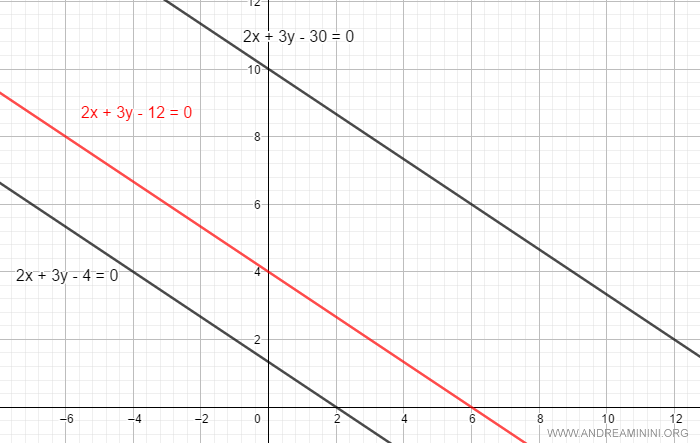
In forma parametrica, la stessa retta è rappresentata come:
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + t \cdot \begin{pmatrix} l \\ m \end{pmatrix} $$
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ -\frac{2}{3} \end{pmatrix} $$
Modificando l'intercetta (0,4) e mantenendo invariato il vettore direttore, si generano tutte le rette del fascio.
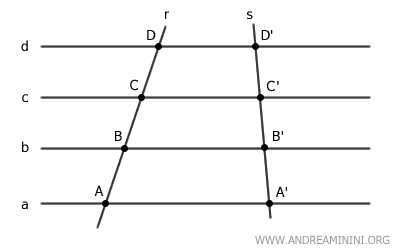
La trasversale del fascio di rette improprio
La trasversale del fascio di rette è una retta che interseca tutte le rette parallele nel fascio di rette improprio.
Ad esempio, la retta r è una trasversale del fascio di rette.
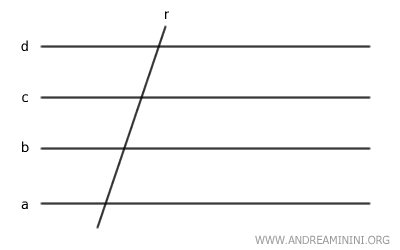
Quando due trasversali distinte intersecano un fascio di rette improprio, i punti di intersezione delle trasversali con le rette parallele sono detti punti corrispondenti.
Ad esempio, i punti A e A' sono due punti corrispondenti.
I segmenti che hanno come estremi due punti corrispondenti della stessa trasversale sono detti segmenti corrispondenti.
Ad esempio, i segmenti AB e BC sono due segmenti corrispondenti.
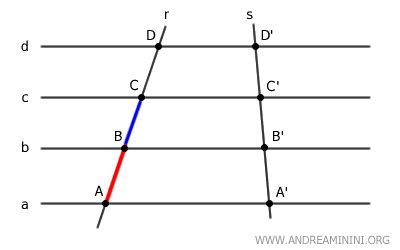
Allo stesso modo sono due segmenti corrispondenti i segmenti A'B' e B'C' della seconda trasversale.
In base al Teorema di Talete, quando un fascio di rette parallele interseca due rette trasversali, si instaura una proporzionalità diretta tra i segmenti corrispondenti di una trasversale e quelli dell'altra trasversale.
Ad esempio, il segmento AB sta al segmento CD come il segmento A'B' sta al segmento C'D'
$$ AB:CD = A'B':C'D' $$
Questa proporzionalità diretta è detta corrispondenza di Talete.
E così via.
