Retta perpendicolare a un piano

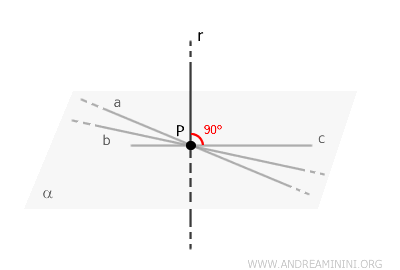
Una retta \( r \) è perpendicolare al piano \( \alpha \) quando è incidente al piano ed è perpendicolare a tutte le rette del piano.

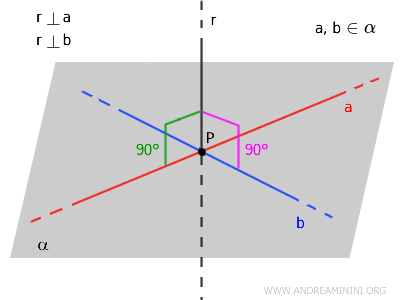
Una retta \( r \) perpendicolare a un piano \( \alpha \) soddisfa due condizioni:

• La retta \( r \) interseca il piano \( \alpha \) è incidente al piano ossia lo interseca in uno e un solo punto $ P $ del piano.
• La retta \( r \) è perpendicolare a tutte le rette del piano \( \alpha \) che passano per il punto di intersezione $ P $.

Nota. Una retta che interseca il piano in un punto ma non è perpendicolare, è detta retta obliqua al piano.

Note a margine

Alcune note e osservazioni aggiuntive sulla perpendicolarità tra rette e piani.

• Teorema delle perpendicolari
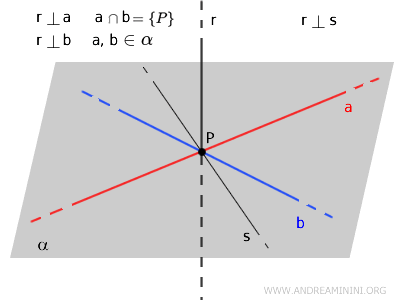
  Se da un punto \( P \) appartenente a una retta \( r \) si tracciano due rette \( a \) e \( b \) perpendicolari a \( r \), allora \( r \) risulta perpendicolare a qualsiasi altra retta \( s \) che passa per \( P \) e giace sul piano \( \alpha \) individuato dalle rette \( a \) e \( b \).
  
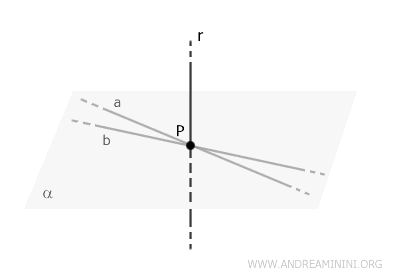
• Teorema delle perpendicolari di una retta nello spazio
  Nello spazio tutte le rette perpendicolari a una retta r passanti per un suo punto P appartengono a un unico piano.
  
• Teorema delle tre rette perpendicolari
  Data una retta \( r \) perpendicolare a un piano \( \alpha \), se dal piede della perpendicolare \( H \) traccio una retta \( t \) perpendicolare a una retta \( s \) del piano \( \alpha \), allora la retta \( s \) risulta perpendicolare anche al piano \( \beta \) definito dalle rette \( r \) e \( t \).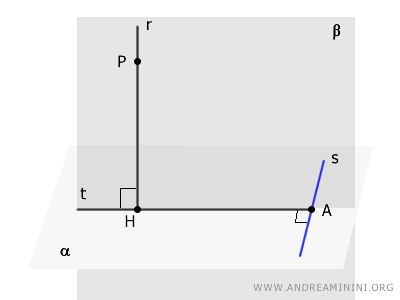

  

• Teorema della retta perpendicolare a un piano
  In un punto qualsiasi \( P \) del piano \( \alpha \) passa un'unica retta \( r \) perpendicolare al piano.
  
• Teorema delle rette perpendicolari al piano
  Due rette perpendicolari allo stesso piano sono parallele tra loro.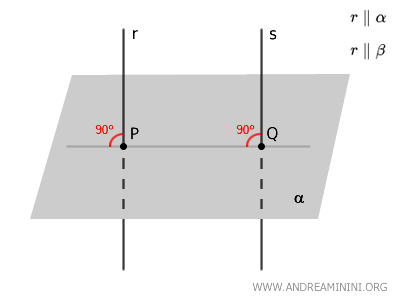

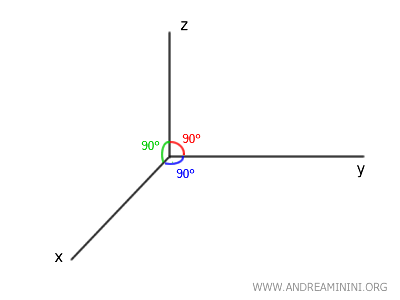
  Nota. Nello spazio (3 dimensioni) non vale il teorema in base al quale due rette perpendicolari a una stessa retta sono parallele tra loro. Quest'ultimo vale solo sul piano (2 dimensioni). Ad esempio, le rette x, y, z che formano il diagramma cartesiano sono perpendicolari tra loro nello spazio $ x \perp y $, $ x \perp z $, $ y \perp z $ ma non sono parallele.
  

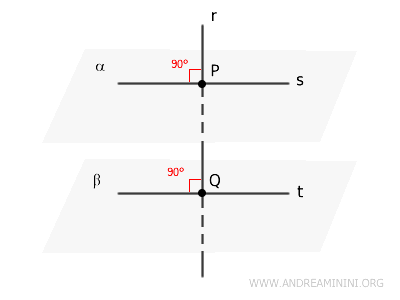
• Teorema della retta perpendicolare a due piani
  Se una retta è perpendicolare a due piani in due punti distinti della retta, allora i due piani sono paralleli.
  

E così via.