Il teorema del fascio improprio di rette
Se un fascio di rette parallele è intersecato da due rette trasversali, ai segmenti congruenti su una trasversale corrispondono dei segmenti congruenti sull'altra trasversale.
Un esempio pratico
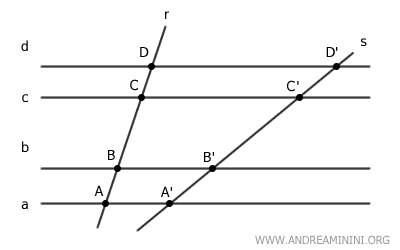
Ad esempio, considero un fascio di rette improprio (a,b,c,d) e due rette trasversali r e s.

Nota. Per fascio di rette improprio si intende un insieme di rette parallele tra loro. Ad esempio, le rette a, b, c, d sono tutte parallele tra loro.
Le rette parallele intersecano la trasversale r nei punti A, B, C, D e la trasversale s nei punti A', B', C', D'.
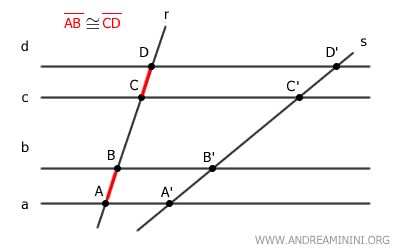
Per ipotesi, i segmenti AB e CD sulla trasversale r sono congruenti, ossia hanno la stessa lunghezza AB≅CD.
$$ \overline{AB} \cong \overline{CD} $$
In base al teorema al teorema del fascio improprio di rette, a questi segmenti congruenti AB≅CD corrispondono dei segmenti congruenti A'B'≅C'D' sull'altra trasversale s.
$$ \overline{A'B'} \cong \overline{C'D'} $$
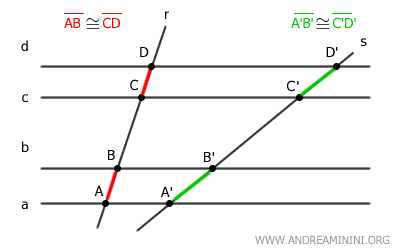
Gli estremi dei segmenti corrispondenti sull'altra trasversale A'B' e C'D' sono individuati dalle rette parallele che intersecano gli stessi estremi dei segmenti AB e CD sulla prima trasversale.
Ad esempio, la retta "a" passa sia per il punto A che per il punto A', ossia per l'estremo inferiore dei segmenti AB e A'B'.
La dimostrazione
Per ipotesi iniziale considero un fascio di rette parallele (a,b,c) e due rette trasversali r e s e due segmenti corrispondenti congruenti AB≅BC sulla trasversale r.
$$ \overline{AB} \cong \overline{AB} $$
Devo dimostrare che esistono due segmenti corrispodenti congruenti A'B'≅B'C' anche sulla trasversale s (tesi).
Per dimostrare il teorema prendo in considerazione due casi: le trasversali sono parallele oppure incidenti
A] Le trasversali sono parallele
In questo caso, per ipotesi iniziale le rette r e s sono rette parallele tra loro ossia r||s.
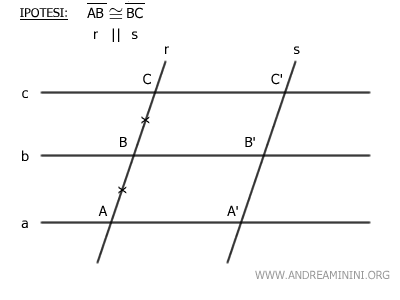
Poiché le trasversali sono parallele, deduco che i segmenti AA', BB' e CC' sono congruenti ossia AA'≅BB'≅CC'.
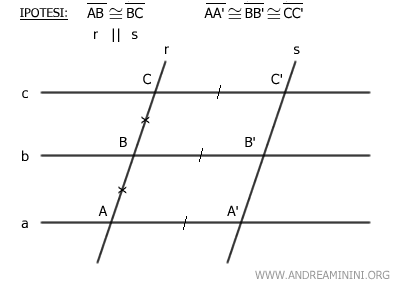
La figura AA'B'B è un parallelogramma perché entrambi lati opposti sono paralleli per definizione del fascio improprio di rette a||b||c e per l'ipotesi iniziale r||s.
Anche la figura BB'C'C è un parallelogramma per le stesse ragioni.
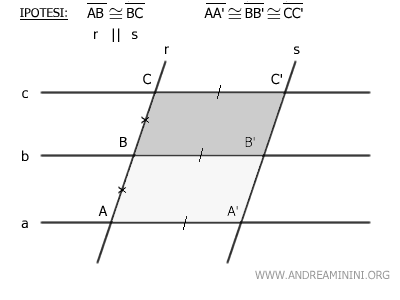
Sapendo che i lati obliqui dei due parallelogrammi AB≅BC sono congruenti per l'ipotesi iniziale e anche le loro basi sono congruenti AA'≅BB', deduco che i due parallelogrammi sono congruenti AA'B'B≅BB'C'C.
$$ AA'B'B \cong BB'C'C $$
Pertanto, i due parallelogrammi hanno i lati e gli angoli congruenti nello stesso ordine.
In particolar modo mi interessa sapere che sono congruenti i lati obliqui AB≅A'B' e BC≅B'C'
$$ \overline{AB} \cong \overline{A'B'} $$
$$ \overline{BC} \cong \overline{B'C'} $$
Sapendo per l'ipotesi iniziale che AB≅BC deduco per la proprietà transitiva che anche i lati A'B'≅B'C' sono congruenti.
$$ \overline{A'B'} \cong \overline{B'C'} $$
In conclusione, ho dimostrato che i segmenti corrispondenti A'B' e B'C' sulla trasversale s sono congruenti se le due trasversali sono parallele.
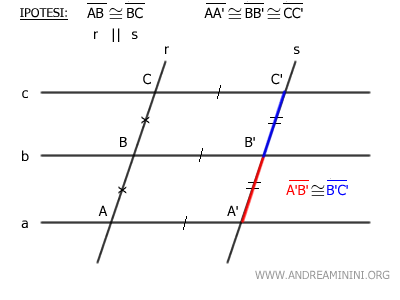
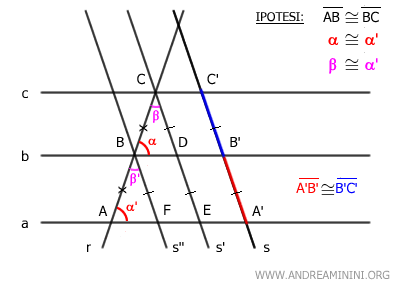
B] Le trasversali non sono parallele
In questo caso, per ipotesi iniziale le rette r e s sono rette incidenti (non parallele).
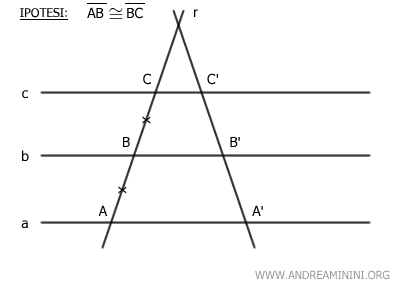
Traccio la retta s' parallela della retta s facendola intersecare con la retta r nel punto C
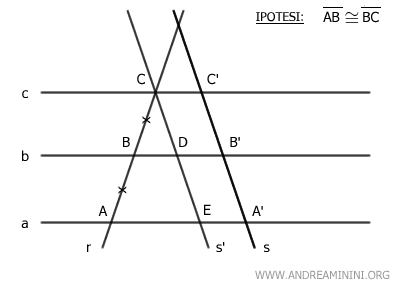
Poi traccio una seconda retta s'' parallela a s che passa per il punto B.
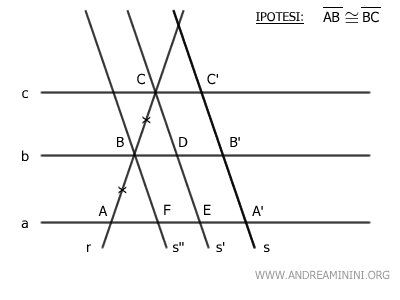
La figura CDB'C' è un parallelogramma e, per definizione, ha i lati opposti congruenti.
Quindi deduco che CD≅B'C'
$$ \overline{CD} \cong \overline{B'C'} $$
Anche La figura BFA'B'è un parallelogramma e ha i lati opposti congruenti.
Quindi deduco che BF≅A'B'
A questo punto analizzo i due triangoli ABF e BCD.
I due triangoli hanno un lato congruente AB≅BC per l'ipotesi iniziale.
Inoltre, hanno gli angoli corrispondenti α≅α' congruenti per il teorema delle rette parallele, perché le rette parallele "a" e "b" sono tagliate dalla retta trasversale s''.
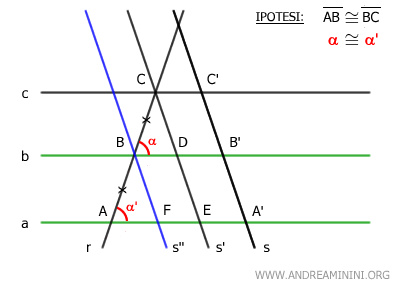
Anche gli angoli corrispondenti β≅β' sono corrispondenti per il teorema delle rette parallele, perché le rette parallele s' e s'' sono tagliate dalla retta trasversale r.
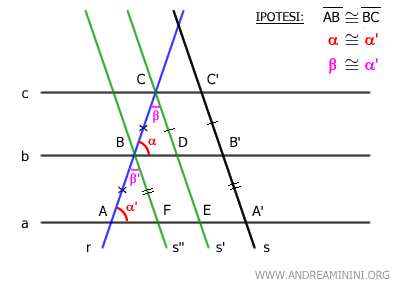
I triangoli ABD≅BCD sono congruenti per il secondo criterio di congruenza (ALA) perché hanno un lato congruente AB≅BC e due angoli congruenti α≅α' e β≅β'
Di conseguenza, i due triangoli hanno tutti i lati e gli angoli congruenti.
In particolar modo mi è utile sapere che sono congruenti i lati BF≅CD
$$ \overline{BF} \cong \overline{CD} $$
Sapendo che CD≅B'C' e BF≅A'B' per la proprietà transitiva deduco che A'B'≅B'C'
$$ \overline{A'B'} \cong \overline{B'C'} $$
In conclusione, ho dimostrato che i segmenti corrispondenti A'B' e B'C' sulla trasversale s sono congruenti se le due trasversali sono incidenti.
E così via.
