La distanza tra due rette

Per distanza tra due rette si intende la distanza minima tra i punti delle rette. $$ d(r_1, r_2) := min(P_{r1}, P_{r2}) $$

Per misurare la distanza tra due rette parallele prendo un punto P(x₀;x₀) di una retta e misuro la distanza tra il punto P e l'altra retta $ ax+by+c=0 $

$$ d = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} $$

In alternativa, se conosco il coefficiente angolare m di due rette parallele $ y=mx+q_1 $ e $ y=mx+q_2 $

$$ d = \frac{|q_2-q_1|}{\sqrt{1+m^2}} $$

Possono verificarsi i seguenti casi:

• Distanza nulla. Se la distanza minima è nulla, le due rette sono coincidenti ( se linearmente dipendenti ) oppure incidenti ( se linearmente indipendenti ).
• Distanza finita. Se la distanza minima è un numero positivo finito, le due rette sono parallele.

Questo schema fornisce una buona sintesi delle varie possibilità.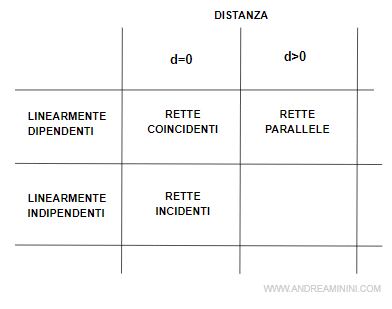

Come calcolare la distanza tra le rette

Per prima cosa devo capire se sono parallele, coincidenti o incidenti tramite lo studio della dipendenza lineare dei vettori direttori

1] Rette linearmente dipendenti

Se i vettori direttori sono linearmente dipendenti, le rette sono coincidenti oppure parallele.

Come capire se sono coincidenti o parallele?

Prendo un punto della prima retta di una retta e calcolo la distanza con l'altra retta.

• Parallele ( d>0 ). Se la distanza è maggiore di zero le rette sono parallele.
• Coincidenti ( d=0 ). Se la distanza è nulla le rette sono coincidenti.

2] Rette linearmente indipendenti

Se i vettori direttori sono linearmente indipendenti, le rette sono sempre incidenti.

Quindi, esiste un solo punto in comune ( punto di incidenza ) tra le due rette.

La distanza minima è nulla.

Esempi pratici

Esempio 1

Ho due rette:

$$ r_1: 5x+3y-6=0 $$

$$ r_2: -4x+4y-8=0 $$

Come prima cosa verifico se sono linearmente indipendenti.

Prendo i rispettivi vettori normali.

$$ n_1 = \begin{pmatrix} 5 \\ 3 \end{pmatrix} $$

$$ n_2 = \begin{pmatrix} -4 \\ 4 \end{pmatrix} $$

Nota. La dipendenza lineare può essere verificata indifferentemente con i vettori normali o con i vettori direttori. Essendo vettori ortogonali, se i vettori normali sono linearmente indipendenti, lo sono anche i vettori direttori. E viceversa.

Poi calcolo il determinante della matrice dei vettori per capire se sono linearmente indipendenti.

$$ det \begin{pmatrix} 5 & -4 \\ 3 & 4 \end{pmatrix} = 20 + 12 = 32 $$

Il determinante è diverso da zero.

Questo vuol dire i due vettori sono linearmente indipendenti.

Pertanto, le due rette sono incidenti e la distanza minima è nulla.

 

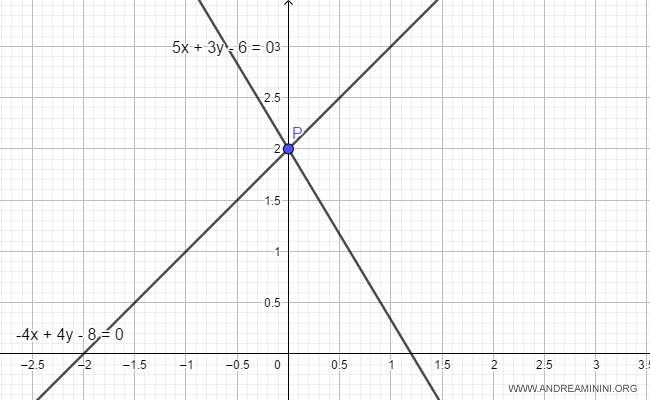
Nota. Per trovare il punto di incidenza basta risolvere il sistema composto da entrambe le equazioni delle rette: $$ \begin{cases} 5x+3y-6=0 \\ -4x+4y-8=0 \end{cases} $$ $$ \begin{cases} x=\frac{6-3y}{5} \\ -4(\frac{6-3y}{5})+4y-8=0 \end{cases} $$ $$ \begin{cases} x=\frac{6-3y}{5} \\ y=2 \end{cases} $$ $$ \begin{cases} x=\frac{6-3(2)}{5} \\ y=2 \end{cases} $$ $$ \begin{cases} x=0 \\ y=2 \end{cases} $$

Esempio 2

Ho due rette:

$$ r_1: 5x+3y-6=0 $$

$$ r_2: 15x+9y-3=0 $$

Come prima cosa verifico se sono linearmente indipendenti.

Prendo i rispettivi vettori normali.

$$ n_1 = \begin{pmatrix} 5 \\ 3 \end{pmatrix} $$

$$ n_2 = \begin{pmatrix} 15 \\ 9 \end{pmatrix} $$

Poi calcolo il determinante della matrice dei vettori per capire se sono linearmente indipendenti.

$$ det \begin{pmatrix} 5 & 15 \\ 3 & 9 \end{pmatrix} = 45 -45= 0 $$

Il determinante è uguale a zero.

Questo significa che i due vettori sono linearmente dipendenti.

Pertanto, le due rette possono essere parallele oppure coincidenti.

Come capire se sono parallele o coincidenti?

Prendo un punto qualsiasi della retta r₁.

Ad esempio

$$ P = \begin{pmatrix} 0 \\ 2 \end{pmatrix} $$

Poi calcolo la distanza tra il punto P e l'altra retta r₂.

$$ D(P(x_0,y_0),r_2) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} $$

$$ D(P(0,2),r_2) = \frac{|15x+9y-3|}{\sqrt{15^2+9^2}} $$

$$ D(P(0,2),r_2) = \frac{|15(0)+9(2)-3|}{\sqrt{225+81}} $$

$$ D(P(0,2),r_2) = \frac{|15|}{\sqrt{306}} = 0.86 $$

La distanza tra il punto P e la retta r₂ è maggiore di zero.

Pertanto, le due rette sono parallele.

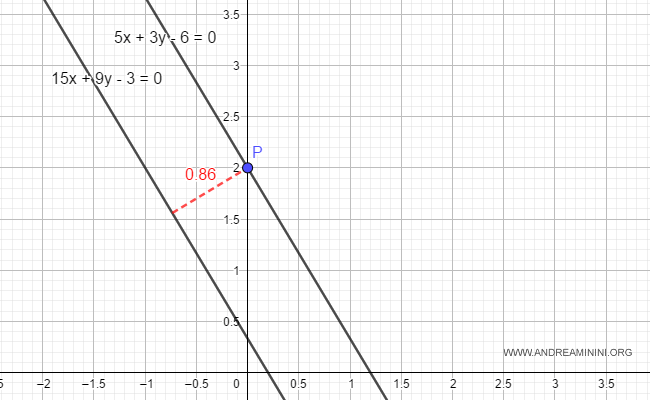
Nota. Se la distanza fosse stata nulla le due rette sarebbero state coincidenti.