Come verificare se due rette sono incidenti, parallele o coincidenti

Per verificare la relazione tra due rette nel piano cartesiano $$ r: ax + by + c = 0 $$ $$ r': a'x + b'y + c' = 0 $$ esamino le loro equazioni in forma generale e confronto i loro coefficienti e termini noti.

• Rette incidenti
  Se il rapporto tra i coefficienti non è proporzionale, le due rette sono incidenti, ovvero hanno un solo punto in comune. $$ \frac{a}{a'} \ne \frac{b}{b'} $$
• Rette parallele e distinte
  Se il rapporto tra i coefficienti è proporzionale, ma il rapporto tra i termini noti è diverso, le due rette sono parallele e distinte, ovvero non hanno punti in comune. $$ \frac{a}{a'} = \frac{b}{b'} \ne \frac{c}{c'} $$
• Rette coincidenti
  Se il rapporto tra i coefficienti è proporzionale ed è uguale al rapporto tra i termini noti, le due rette sono coincidenti, ovvero hanno tutti i punti in comune. $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} $$

Nota. Queste formule derivano direttamente dall'applicazione del criterio di parallelismo $$ \frac{a}{a'} = \frac{b}{b'} $$ e del criterio di coincidenza delle rette $$ \frac{a}{a'} = \frac{b}{b'} \ne \frac{c}{c'} $$

Un esempio pratico

Considero due rette con le equazioni in forma impropria

$$ r: 2x + 3y + 4 = 0 $$

$$ r': 4x + 6y + 12 = 0 $$

Per prima cosa verifico se soddisfano il criterio di parallelismo delle rette, analizzando il rapporto tra i coefficienti a=2, b=3 e a'=4 e b'=6 delle variabili x e y nelle due equazioni.

$$ \frac{a}{a'} = \frac{2}{4} = \frac{1}{2} $$

$$ \frac{b}{b'} = \frac{3}{6} = \frac{1}{2} $$

Il rapporto tra i coefficienti è proporzionale, quindi le due rette non sono incidenti.

$$ \frac{a}{a'} = \frac{b}{b'} = \frac{1}{2} $$

Questo significa che le due rette sono parallele, ma non so ancora se sono distinte o coincidenti.

Per capirlo devo verificare se le rette soddisfano anche il criterio di coincidenza, analizzando il rapporto tra i termini noti c=4 e c'=12.

$$ \frac{c}{c'} = \frac{4}{12} = \frac{1}{3} $$

Il rapporto tra i termini noti non è uguale al rapporto dei coefficienti, quindi le rette non soddisfano il criterio di coincidenza.

$$ \frac{c}{c'} = \frac{1}{3} \ne \frac{1}{2} = \frac{a}{a'} = \frac{b}{b'} $$

Questo significa che le rette non sono coincidenti.

Deduco per esclusione che le due rette sono parallele distinte.

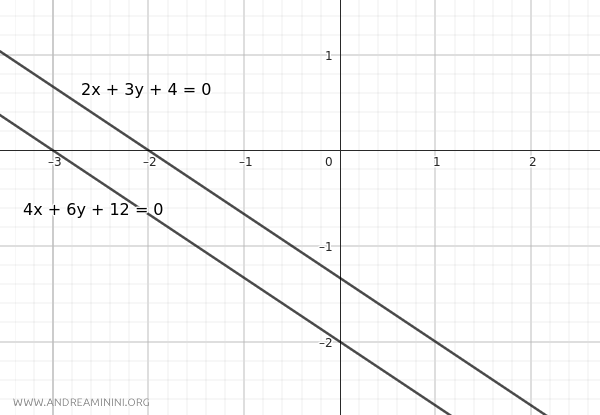
Esempio 2

In questo esempio prendo in considerazione due rette:

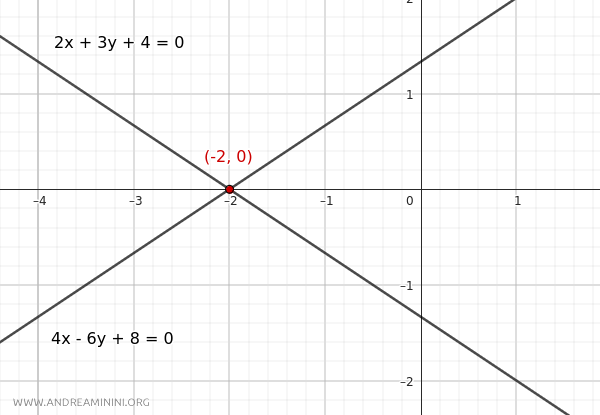
$$ r: 2x + 3y + 4 = 0 $$

$$ r': 4x - 6y + 8 = 0 $$

Per capire se sono incidenti o parallele, controllo se soddisfano la condizione di parallelismo.

$$ \frac{a}{a'} = \frac{2}{4} = \frac{1}{2} $$

$$ \frac{b}{b'} = \frac{3}{-6} = - \frac{1}{2} $$

In questo caso la condizione di parallelismo $ \frac{a}{a'} = \frac{b}{b'} $ non è soddisfatta

$$ \frac{1}{2} \ne  - \frac{1}{2} $$

Quindi, le due rette sono incidenti. Si incontrano in un unico punto che hanno in comune.

Qual è il punto di intersezione delle rette incidenti?

Per trovarlo occorre risolvere il seguente sistema di equazioni lineari:

$$ \begin{cases} 2x + 3y + 4 = 0  \\ \\  4x - 6y + 8 = 0   \end{cases} $$

Risolvo il sistema usando il metodo per sostituzione. Qualsiasi altro metodo di risoluzione sarebbe comunque andato bene.

Ad esempio, ricavo la variabile x nella prima equazione e la sostituisco nella seconda equazione.

$$ \begin{cases} x  = \frac{ -4 - 3y}{2}  \\ \\  4x - 6y + 8 = 0   \end{cases} $$

$$ \begin{cases} x  = \frac{ -4 - 3y}{2}  \\ \\  4 \cdot ( \frac{ -4 - 3y}{2}  )  - 6y + 8 = 0   \end{cases} $$

$$ \begin{cases} x  = \frac{ -4 - 3y}{2}  \\ \\  \frac{ -16 - 12y}{2}  - 6y + 8 = 0   \end{cases} $$

$$ \begin{cases} x  = \frac{ -4 - 3y}{2}  \\ \\  \frac{ -16 - 12y - 12y + 16}{2}  = 0   \end{cases} $$

$$ \begin{cases} x  = \frac{ -4 - 3y}{2}  \\ \\  \frac{ - 24y}{2}  = 0   \end{cases} $$

$$ \begin{cases} x  = \frac{ -4 - 3y}{2}  \\ \\  -12y = 0   \end{cases} $$

$$ \begin{cases} x  = \frac{ -4 - 3y}{2}  \\ \\  -12y \cdot ( - \frac{1}{12} ) = 0 \cdot ( - \frac{1}{12} )   \end{cases} $$

$$ \begin{cases} x  = \frac{ -4 - 3y}{2}  \\ \\  y=0   \end{cases} $$

Una volta trovato il valore della variabile y=0 nella seconda equazione, lo sostituisco nella prima equazione del sistema.

$$ \begin{cases} x  = \frac{ -4 - 3 \cdot 0 }{2}  \\ \\  y=0   \end{cases} $$

$$ \begin{cases} x  = \frac{ -4}{2}  \\ \\  y=0   \end{cases} $$

$$ \begin{cases} x  = -2 \\ \\  y=0   \end{cases} $$

La soluzione del sistema è x=-2 e y=0.

Pertanto, le rette incidenti si incontrano nel punto alle coordinate (x;y)=(-2;0) del piano cartesiano.

Il calcolo del determinante

Una formula alternativa e spesso più diretta per determinare la relazione tra due rette si basa sul calcolo del determinante formato dai coefficienti delle variabili \(x\) e \(y\).

$$ D = a \cdot b' - b \cdot a' $$

Dove a,a'b,b' sono i coefficienti delle variabili x e y nelle equazioni generali delle due rette.

$$ r: ax + by + c = 0 $$

$$ r': a'x + b'y + c' = 0 $$

A seconda del valore del determinante, le due rette sono incidenti o non incidenti

• \(D \neq 0\)
  Se il determinante è diverso da zero, le rette sono incidenti ovvero si intersecano in un unico punto.
• \(D = 0\)
  Se il determinante è nullo, le rette non sono incidenti. Quindi possono essere parallele distinte o coincidenti.

Quando il determinante è nullo \(D = 0\), le rette soddisfano il criterio di parallelismo.

$$ \frac{a}{a'} = \frac{b}{b'} $$

Resta da capire se soddisfano anche il criterio di coincidenza oppure no.

In questo caso, calcolo il rapporto tra i termini noti e controllo se \( \frac{c}{c'} \) è uguale al rapporto \( \frac{a}{a'} \) e \( \frac{b}{b'} \).

• Se \( \frac{c}{c'} = \frac{a}{a'} = \frac{b}{b'} \) le rette sono coincidenti. Hanno tutti i punti in comune.
• Se il rapporto \(\frac{c}{c'}\) è diverso o se uno dei rapporti non esiste (perché il denominatore è zero mentre il numeratore non lo è) le rette sono parallele distinte.

Esempio

Considero le seguenti rette:

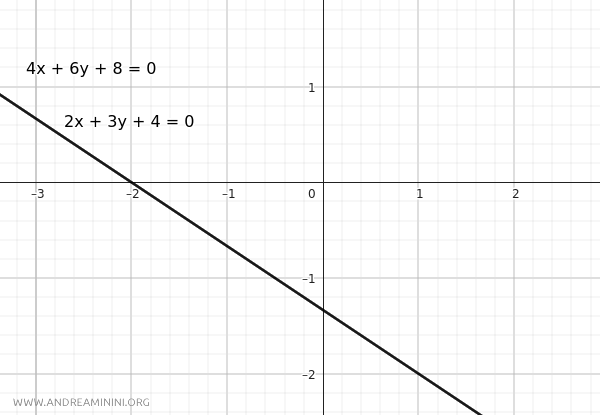
$$ r: 2x + 3y + 4 = 0 $$

$$ r': 4x + 6y + 8 = 0 $$

Calcolo il determinante

$$ D = 2 \times 6 - 3 \times 4 = 12 - 12 = 0 $$

Dato che \(D = 0\), le rette non sono incidenti. Quindi, sono parallele.

Ora verifico se sono coincidenti o distinte.

$$ \frac{2}{4} = \frac{3}{6} = \frac{4}{8} = \frac{1}{2} $$

Tutti i rapporti sono uguali, quindi le rette sono coincidenti.

In questo modo posso analizzare la relazione tra due rette basandomi sui coefficienti e i termini noti delle loro equazioni lineari, senza dover risolvere un sistema di equazioni lineari.

E così via.