Equazione goniometrica tan(a)=-tan(b)
L'equazione goniometrica $$ \tan \alpha = - \tan \alpha' $$ si risolve con la formula $$ \tan \alpha = \tan (-\alpha') $$ le cui soluzioni sono $$ \alpha = (-\alpha') + k \pi $$ Dove k è un numero intero qualsiasi nell'intervallo (-∞, ∞).
La tangente è una funzione periodica con periodo π radianti.
Quindi, l'equazione goniometrica tan(α)=-tan(α') ha infinite soluzioni considerando i multipli interi k di un angolo piatto π.
Un esempio pratico
Devo risolvere l'equazione goniometrica
$$ \tan \frac{1}{2} x = - \tan \frac{3}{2} x $$
Essendo la tangente una funzione dispari, posso sostituire -tan(3/2x)=tan(-3/2x)
$$ \tan \frac{1}{2} x = \tan -\frac{3}{2} x $$
In questo modo l'equazione diventa del tipo tan(α)=tan(α')
$$ \alpha = \frac{1}{2} x $$ $$ \alpha' = -\frac{3}{2} x $$
Questo mi permette di applicare la stessa formula di risoluzione di un'equazione tan(α)=tan(α')
$$ \alpha = \alpha' + k \pi $$
Sostituisco α e α' con gli argomenti delle tangenti
$$ \frac{1}{2} x = ( -\frac{3}{2} x ) + k \pi $$
Poi metto in evidenza l'incognita x
$$ \frac{1}{2} x +\frac{3}{2} x = k \pi $$
$$ \frac{1+3}{2} x = k \pi $$
$$ \frac{4}{2} x = k \pi $$
$$ 2 x = k \pi $$
$$ x = \frac{1}{2} k \pi $$
Ho trovato le infinite soluzioni dell'equazione goniometrica, dove k è un numero intero qualsiasi.
Per trovare le prime soluzioni mi basta variare la variabile k.
Verifico per k=0
$$ x = \frac{1}{2} k \pi $$
$$ x = \frac{1}{2} (0) \pi $$
$$ x = 0 $$
La prima soluzione dell'equazione goniometrica è la soluzione banale x=0.
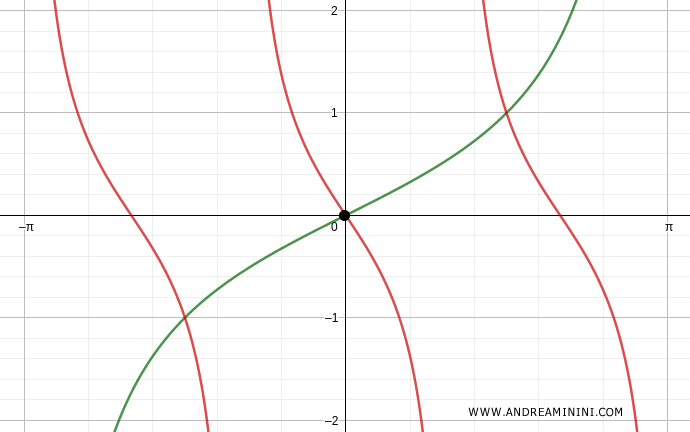
Verifico per k=1
$$ x = \frac{1}{2} k \pi $$
$$ x = \frac{1}{2} (1) \pi $$
$$ x = \frac{1}{2} \pi $$
La seconda soluzione è x=1/2π
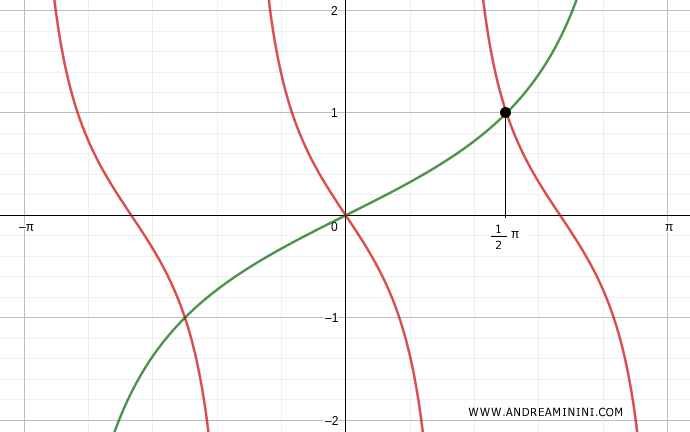
Verifico per k=-1
$$ x = \frac{1}{2} k \pi $$
$$ x = \frac{1}{2} (-1) \pi $$
$$ x = -\frac{1}{2} \pi $$
La terza soluzione è x=-1/2 π
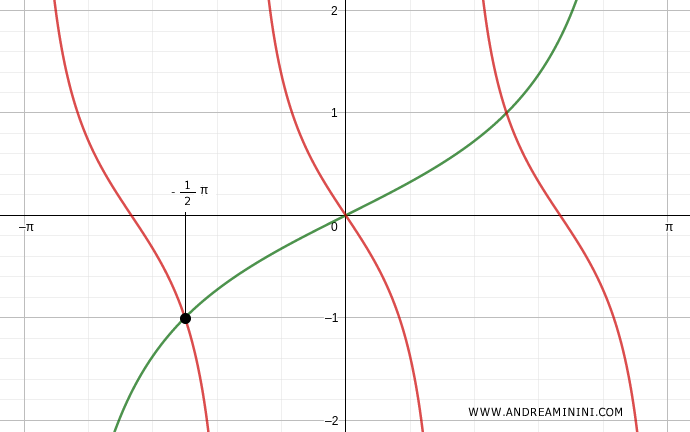
Continuando a variare k=2, -2, 3, ... trovo le altre infinite soluzioni dell'equazione goniometrica.
La dimostrazione
La tangente è una funzione dispari
$$ - \tan \alpha= \tan (-\alpha) $$
Dal punto di vista grafico
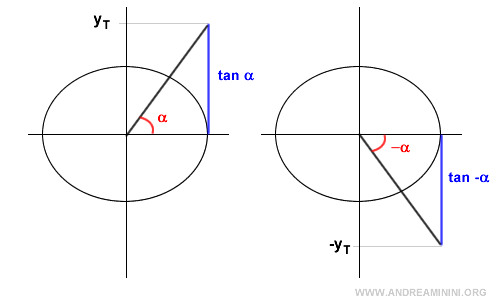
Pertanto, un'equazione goniometrica in cui compare la tangente -tan(α')
$$ \tan \alpha = - \tan \alpha' $$
posso riscriverla in una forma equivalente sostituendo -tan(α') con tan(-α')
$$ \tan \alpha = - \tan \alpha' = \tan (- \alpha') $$
$$ \tan \alpha = \tan (- \alpha') $$
Questo mi permette di risolvere l'equazione goniometrica come se fosse un caso tan α = tan α'
$$ \alpha = \alpha' + k \pi $$
Dove k è un numero intero qualsiasi che moltiplica pi greco radianti (180°) perché la tangente è una funzione periodica con periodo π radianti.
In questo caso l'argomento della tangente è l'angolo opposto -α'
$$ \alpha = (-\alpha') + k \pi $$
Questo dimostra la formula di risoluzione dell'equazione goniometrica.
E così via.
