L'equazione goniometrica del tipo sin(α)=-sin(α')

L'equazione goniometrica $$ \sin \alpha = - \sin \alpha' $$ si risolve con la formula $$ \sin \alpha = \sin(- \alpha' ) $$ le cui soluzioni sono $$ α = (-α') + 2k \pi \ ∨ \ α+(-α') = \pi + 2k \pi $$

Un esempio

Devo risolvere l'equazione goniometrica

$$ \sin(\frac{1}{2}x) = - \sin(\frac{1}{6}x) $$

Il seno è una funzione dispari.

Quindi posso riscrivere l'equazione in questa forma equivalente considerando -sin(1/6x) = sin(-1/6x)

$$ \sin(\frac{1}{2}x) = \sin( - \frac{1}{6}x) $$

In questo modo l'equazione goniometrica diventa del tipo sin(α)=sin(α') con gli angoli

$$ \alpha = \frac{1}{2}x \\ \alpha' = - \frac{1}{6}x $$

Questo mi permette di applicare la stessa formula di risoluzione di un'equazione sin(α)=sin(α')

$$ α = α' + 2k \pi \ ∨ \ α+α' = \pi + 2k \pi $$

Sostituisco α e α' con gli argomenti del seno dell'equazione goniometrica e metto in evidenza l'incognita x

$$ \frac{1}{2}x = -\frac{1}{6}x + 2k \pi \ ∨ \ \frac{1}{2}x + (-\frac{1}{6}x) = \pi + 2k \pi $$

$$ \frac{1}{2}x + \frac{1}{6}x = 2k \pi \ ∨ \ \frac{1}{2}x -\frac{1}{6}x = \pi + 2k \pi $$

$$ \frac{3+1}{6}x = 2k \pi \ ∨ \ \frac{3-1}{6}x = \pi + 2k \pi $$

$$ \frac{4}{6}x = 2k \pi \ ∨ \ \frac{2}{6}x = \pi + 2k \pi $$

$$ \frac{2}{3}x = 2k \pi \ ∨ \ \frac{1}{3}x = \pi + 2k \pi $$

$$ x = \frac{3}{2} \cdot 2k \pi \ ∨ \ x = 3 \cdot ( \pi + 2k \pi ) $$

$$ x = 3k \pi \ ∨ \ x =3 \pi + 6k \pi $$

Ho trovato le infinite soluzioni dell'equazione goniometrica, dove k è un numero intero qualsiasi (positivo, nullo o negativo).

A questo punto trovo le soluzioni per k=0

$$ x = 3(0) \pi \ ∨ \ x =3 \pi + 6(0) \pi $$

$$ x = 0 \ ∨ \ x =3 \pi $$

Per k=0 l'equazione goniometrica ha due soluzioni x=0 e x=3π

La prima soluzione x=0 è banale

$$ \sin(\frac{1}{2}x) = - \sin(\frac{1}{6}x) $$

$$ \sin(\frac{1}{2} \cdot 0) = - \sin(\frac{1}{6} \cdot 0) $$

$$ \sin(0)=\sin(0) $$

$$ 0 = 0 $$

Questo vuol dire che le due funzioni si eguagliano nell'origine (x=0)

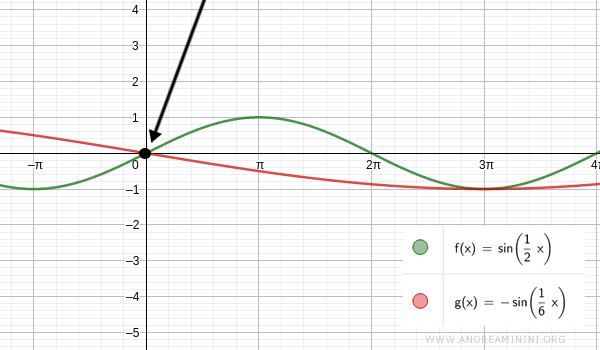
La seconda soluzione è x=3π

$$ \sin(\frac{1}{2}x) = - \sin(\frac{1}{6}x) $$

$$ \sin(\frac{1}{2} \cdot 3 \pi) = - \sin(\frac{1}{6} \cdot 3 \pi ) $$

$$ \sin(\frac{3}{2} \pi) = - \sin(\frac{1}{2} \pi ) $$

$$ -1 = - 1 $$

Le due funzioni si eguagliano anche per x=3π

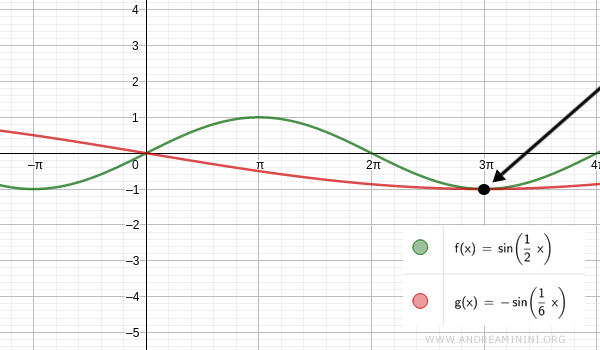
Le altre infinite soluzioni dell'equazione goniometrica si trovano considerando k=-1, k=2, k=-2, k=3, ecc.

La dimostrazione

La funzione seno è una funzione dispari.

$$ \sin ( - \gamma) = - \sin ( \gamma ) $$

Pertanto, l'equazione goniometrica

$$ \sin \alpha = - \sin ( \alpha’ ) $$

si può scrivere in forma equivalente sostituendo -sin(a’) con sin(-a’)

$$ \sin \alpha = \sin ( - \alpha‘) $$

In questo modo posso risolvere l'equazione goniometrica come se fosse un caso sin α = sin α'

$$ α = α' + 2k \pi \ ∨ \ α+α' = \pi + 2k \pi $$

con l'angolo opposto -α'

$$ α = (-α') + 2k \pi \ ∨ \ α+(-α') = \pi + 2k \pi $$

E così via.