Equazione goniometrica cos(a)=-cos(b)

L'equazione goniometrica $$ \cos \alpha = -\cos \alpha' $$ si risolve con la formula $$ \cos \alpha = \cos (\pi - \alpha') $$ le cui soluzioni sono $$ \alpha=(\pi - \alpha')+2k \pi \ ∨ \ \alpha = - (\pi - \alpha') + 2k \pi $$

Un esempio

Devo risolvere l'equazione goniometrica

$$ \cos( \frac{1}{2}x) = - \cos ( \frac{3}{4} x ) $$

Riscrivo l'equazione nella forma equivalente

$$ \cos( \frac{1}{2}x ) = \cos ( \pi - \frac{3}{4} x ) $$

In questo modo posso risolverla come se fosse un'equazione cos(α)=cos(α') con gli angoli

$$ \alpha = \frac{1}{2}x $$

$$ \alpha' = \pi - \frac{3}{4} x $$

Questo mi permette di trovare le soluzioni con la stessa formula usata per le equazioni cos(α)=cos(α')

$$ \alpha=\alpha'+2k \pi \ ∨ \ \alpha = - \alpha' + 2k \pi $$

Sostituisco gli angoli α e α'

$$ \frac{1}{2}x =( \pi - \frac{3}{4} x ) +2k \pi \ ∨ \ \frac{1}{2}x = - ( \pi - \frac{3}{4} x ) + 2k \pi $$

$$ \frac{1}{2}x + \frac{3}{4} x = \pi +2k \pi \ ∨ \ \frac{1}{2}x - \frac{3}{4} x = - \pi + 2k \pi $$

$$ \frac{5}{4} x = \pi +2k \pi \ ∨ \ - \frac{1}{4} x = - \pi + 2k \pi $$

$$ x = \frac{4}{5} ( \pi +2k \pi ) \ ∨ \ - x = 4 \cdot ( - \pi + 2k \pi ) $$

$$ x = \frac{4}{5} \pi + \frac{4}{5} \cdot 2k \pi \ ∨ \ - x = - 4 \pi + 8k \pi $$

$$ x = \frac{4}{5} \pi + \frac{4}{5} \cdot 2k \pi \ ∨ \ x = 4 \pi - 8k \pi $$

Ho trovato le infinite soluzioni dell'equazione goniometrica, dove k è un numero intero qualsiasi (positivo, nullo o negativo).

Per trovare tutte le soluzioni mi basta variare la variabile intera k.

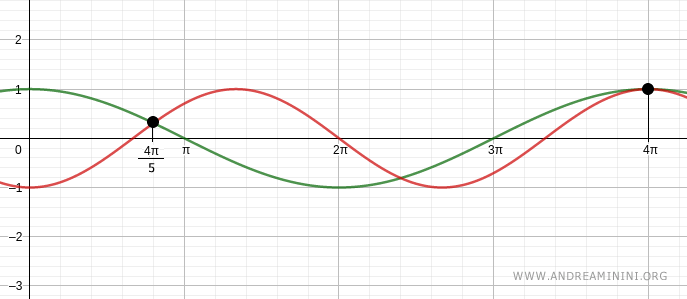
Verifico per k =0

$$ x = \frac{4}{5} \pi + \frac{4}{5} \cdot 2k \pi \ ∨ \ x = 4 \pi - 8k \pi $$

$$ x = \frac{4}{5} \pi + \frac{4}{5} \cdot 2(0) \pi \ ∨ \ x = 4 \pi - 8(0) \pi $$

$$ x = \frac{4}{5} \pi \ ∨ \ x = 4 \pi $$

Quindi le prime due soluzioni sono x=4π/5 e x=4π.

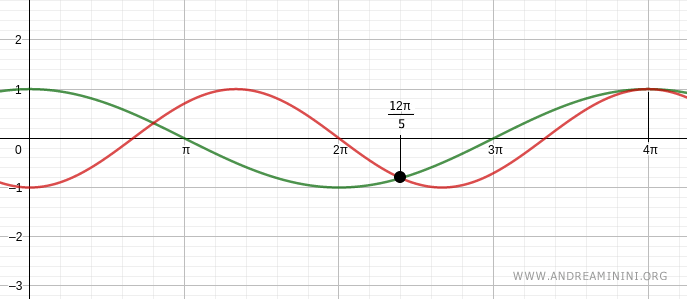
Verifico per k =0

$$ x = \frac{4}{5} \pi + \frac{4}{5} \cdot 2k \pi \ ∨ \ x = 4 \pi - 8k \pi $$

$$ x = \frac{4}{5} \pi + \frac{4}{5} \cdot 2(1) \pi \ ∨ \ x = 4 \pi - 8(1) \pi $$

$$ x = \frac{4}{5} \pi + \frac{8}{5} \pi \ ∨ \ x = 4 \pi - 8 \pi $$

$$ x = \frac{12}{5} \pi \pi \ ∨ \ x = - 4 \pi $$

Altre due soluzioni dell'equazione goniometrica sono x=12/5 e x=-4π

Variando k si possono trovare tutte le altre infinite soluzioni dell'equazione goniometrica.

Dimostrazione

Due angoli α e α' hanno il valore del coseno opposto

$$ \cos \alpha = - \cos \alpha' $$

solo se sono sono angoli supplementari.

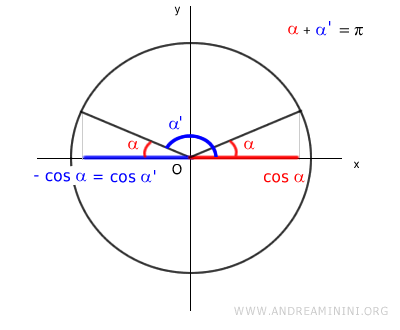
La somma di due angoli supplementari è 180° (ossia π radianti)

$$ \alpha + \alpha' = \pi $$

$$ \alpha = \pi - + \alpha' $$

Quindi posso sostituire α con π-α'

$$ \cos \alpha = - \cos \alpha' $$

$$ \cos (\pi - \alpha') = - \cos \alpha' $$

Mettendo insieme le due equazioni ottengo l'equivalenza

$$ \cos \alpha = - \cos \alpha' = \cos (\pi - \alpha') $$

ossia

$$ \cos \alpha = \cos (\pi - \alpha') $$

In questo modo posso risolvere e risolvere l'equazione goniometrica come se fosse un caso cos(x)=cos(y)

$$ x=y+2k \pi \ ∨ \ x = - y' + 2k \pi $$

Dove x = α mentre y = π - α'

$$ \alpha=(\pi - \alpha')+2k \pi \ ∨ \ \alpha = - (\pi - \alpha') + 2k \pi $$

E così via.