Equazione goniometrica cos (a) = cos (b)

L'equazione goniometrica $$ \cos(\alpha) = \cos(\alpha') $$ è soddisfatta se gli angoli sono congruenti α=α' o gli angoli sono opposti α=-α' $$ \alpha=\alpha'+2k \pi \ ∨ \ \alpha = - \alpha' + 2k \pi $$

Essendo il coseno una funzione periodica con periodo 2π l'equazione goniometrica ha infinite soluzione se considero anche i multipli interi k di un angolo giro 2π

Dove k è un numero intero qualsiasi nell'intervallo (-∞, ∞).

Un esempio pratico

Devo risolvere l'equazione goniometrica

$$ \cos(\frac{1}{2}x) = \cos(\frac{3}{2}x) $$

Gli angoli delle due funzioni coseno sono

$$ \alpha_1 = \frac{1}{2}x $$

$$ \alpha_2 = \frac{3}{2}x $$

Applico la formula dell'equazione goniometrica cos x = cos y

$$ \alpha=\alpha'+2k \pi \ ∨ \ \alpha = - \alpha' + 2k \pi $$

Sostituisco α e α'

$$ \frac{1}{2}x = \frac{3}{2}x +2k \pi \ ∨ \ \frac{1}{2}x = - \frac{3}{2}x + 2k \pi $$

Svolgo i calcoli e metto in evidenza la x

$$ \frac{1}{2}x - \frac{3}{2}x = 2k \pi \ ∨ \ \frac{1}{2}x + \frac{3}{2}x = 2k \pi $$

$$ - x = 2k \pi \ ∨ \ 2x = 2k \pi $$

$$ x = - 2k \pi \ ∨ \ x = \frac{1}{2} \cdot 2k \pi $$

$$ x = - 2k \pi \ ∨\ x = k \pi $$

In questo modo trovo tutte le soluzioni dell'equazione cos x = cos y

Per trovare le soluzioni mi basta variare la costante intera k.

Verifico per k =0

$$ x = - 2k \pi \ ∨ \ x = k \pi $$

$$ x = - 2(0) \pi \ ∨ \ x = (0) \pi $$

$$ x = 0 \ ∨ \ x = 0 $$

Una soluzione dell'equazione goniometrica è x=0

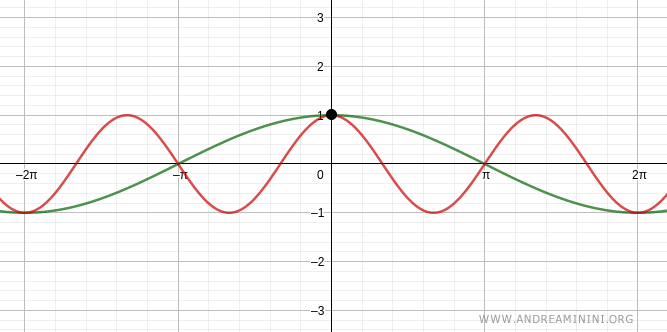
Verifico per k =1

$$ x = - 2k \pi \ ∨ \ x = k \pi $$

$$ x = - 2(1) \pi \ ∨ \ x = (1) \pi $$

$$ x = -2 \pi \ ∨ \ x = \pi $$

Altre due soluzioni sono x=-2π e x=π.

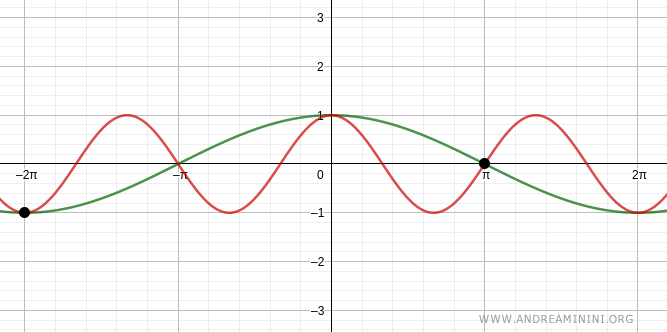
Verifico per k =-1

$$ x = - 2k \pi \ ∨ \ x = k \pi $$

$$ x = - 2(-1) \pi \ ∨ \ x = (-1) \pi $$

$$ x = 2 \pi \ ∨ \ x = -\pi $$

Altre due soluzioni sono x=2π e x=-π.

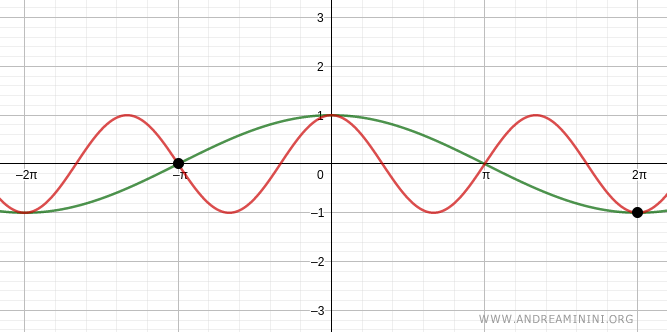
Variando k trovo le infinite soluzioni dell'equazione goniometrica.

La dimostrazione

Considero due angoli α₁ e α₂ che generano lo stesso valore del coseno

$$ \cos \alpha_1 = \cos \alpha_2 = c $$

Due angoli hanno lo stesso valore del coseno in due casi

• se gli angoli sono congruenti (α₁=α₂)
• se gli angoli sono opposti (α₁=-α₂)

Dal punto di vista grafico

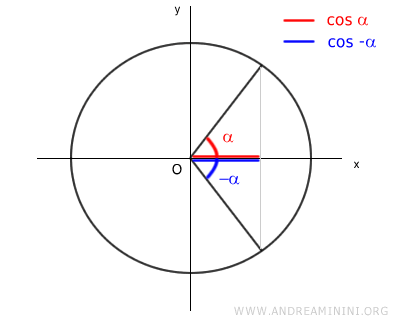
Quindi le condizioni necessarie per avere lo stesso valore del coseno sono

$$ \alpha_1 = \alpha_2 $$

$$ \alpha_1 = - \alpha_2 $$

Il coseno è una funzione periodica con periodo uguale a 2π.

Quindi, devo includere tra le soluzioni anche i multipli interi k dell'angolo giro 2π.

$$ \alpha_1 = \alpha_2 + 2k \pi $$

$$ \alpha_1 = - \alpha_2 + 2k \pi $$

Questo dimostra l'insieme delle soluzioni di un'equazione goniometrica del tipo cos α₁ = cos α₂

$$ α_1 = α_2 + 2k \pi \ ∨ \ α_1 = - α_2 + 2k \pi $$

E così via.