Disequazioni goniometriche

Cos'è una disequazione goniometrica

Le disequazioni goniometriche sono disequazioni in cui l'incognita x è l'argomento di una o più funzioni goniometriche (seno, coseno, tangente, cotangente, ecc. ).

Le disequazioni goniometriche sono dette

• Disequazioni goniometriche elementari
  Sono dette disequazioni goniometriche elementari le disequazioni in cui l'incognita x è l'argomento di una funzione trigonometrica (seno, coseno, tangente, ... ) e un termine noto c. $$ \sin x \le c $$
• Disequazioni goniometriche non elementari
  Sono dette disequazioni goniometriche elementari le disequazioni in cui l'incognita x è l'argomento di due o più funzioni trigonometriche (seno, coseno, tangente, ... ) e un termine noto c. $$ \sin x + \cos x \le c $$

Come risolvere le disequazioni goniometriche

Posso risolvere una disequazione goniometrica

1. Trovo le soluzioni dell'equazione goniometrica associata alla disequazione
2. Individuo quali angoli soddisfano la disequazione

Dal punto di vista grafico disegno il grafico della funzione goniometrica (es. sin x = c ).

Poi traccio la retta y = c e verifico in quali valori dell'incognita x la disequazione è soddisfatta.

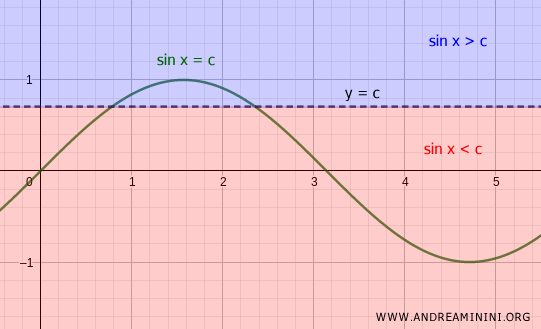
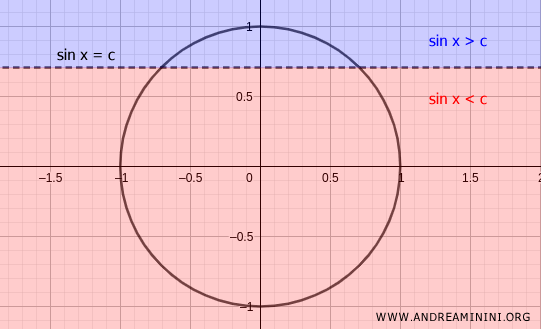
In alternativa, disegno la circonferenza goniometrica e la retta sin x = c.

Poi trovo in quali punti la retta interseca la circonferenza e verifico con quali angoli la disequazione è soddisfatta.

Un esempio pratico

Devo risolvere la disequazione goniometrica elementare

$$ \sin x \le \frac{\sqrt{3}}{2} $$

Studio le soluzioni dell'equazione goniometrica associata

$$ \sin x = \frac{\sqrt{3}}{2} $$

Le soluzioni dell'equazione goniometrica elementare del seno sono

$$ x = \frac{\pi}{3} + 2k \pi \ ∨ \ (\pi - \frac{\pi}{3}) + 2k \pi $$

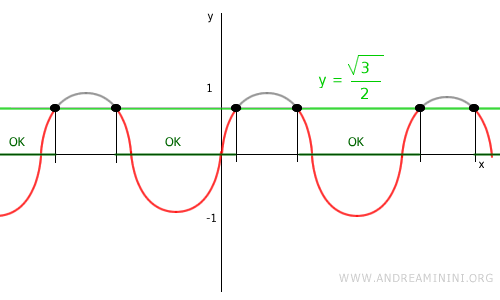
Dal punto di vista grafico, per trovare le soluzioni, ossia gli angoli x, mi basta tracciare una retta y=√3/2 e trovare i punti in cui interseca la circonferenza goniometrica (A e B).

Poi aggiungo 2kπ alle soluzioni per considerare anche le soluzioni periodiche dell'equazione.

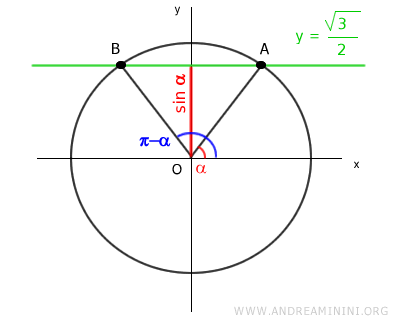
E' subito evidente che la disequazione nel periodo [0 , 2π] è soddisfatta negli intervalli

$$ x \in (0 \ ; \ \frac{\pi}{3} ) \ ∪ \ ( \pi - \frac{\pi}{3} \ ; \; 2 \pi) $$

Nota. In alternativa alla circonferenza goniometrica, disegno il grafico della funzione goniometrica e verifico in quali punti la retta y=√3/2 interseca il grafico.

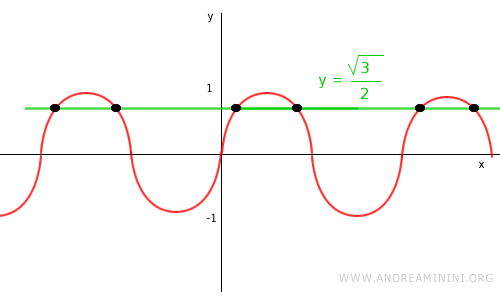
Poi verifico in quali intervalli di x la disequazione è soddisfatta.

Esempio 2

Devo risolvere questa disequazione goniometrica.

$$ 2 \sin^2 x + \sqrt{3} \sin x \ge 0 $$

E' una disequazione goniometrica non elementare.

$$ 2 \sin^2 x + \sqrt{3} \sin x = 0 $$

Utilizzo la tecnica del cambio di variabile t=sin x

$$ 2 t^2 + \sqrt{3} t = 0 $$

Poi trovo le soluzioni dell'equazione di 2° grado con i coefficienti a=2, b=√3, c=0.

$$ t = \frac{-b \pm \sqrt{b^2-4ac} }{2a} $$

$$ t = \frac{-(\sqrt{3}) \pm \sqrt{(\sqrt{3})^2-4(2)(0)} }{2(2)} $$

$$ t = \frac{-\sqrt{3} \pm \sqrt{3}}{4} $$

$$ t = \begin{cases} t_1 = \frac{-\sqrt{3}+\sqrt{3}}{4}=0 \\ \\ t_2 = \frac{-\sqrt{3}-\sqrt{3}}{4} = \frac{-2\sqrt{3}}{4} = - \frac{\sqrt{3}}{2} \end{cases} $$

Le soluzioni dell'equazione di 2° grado sono t₁=0 e t₂=-√3/2.

$$ t_1 = 0 $$

$$ t_2 = -\frac{\sqrt{3}}{2} $$

La disequazione è una parabola rivolta verso il basso perché il coefficiente a>0

Quindi, la disequazione t²+√3·t ≥ 0 è soddisfatta nell'intervallo

$$ t \in ( - \infty, -\frac{\sqrt{3}}{2} ] ∪ [ 0 \ , \ +\infty ) $$

Sapendo che t=sin x

$$ \sin x \in ( - \infty, -\frac{\sqrt{3}}{2} ] ∪ [ 0 \ , \ +\infty ) $$

e considerando il codominio del seno ristretto nell'intervallo [-1, 1]

$$ \sin x \in ( -1 \ , \ -\frac{\sqrt{3}}{2} ] ∪ [ 0 \ , \ 1 ) $$

Uso il metodo grafico per capire sulla circonferenza goniometrica in quali angoli la disequazione è soddisfatta.

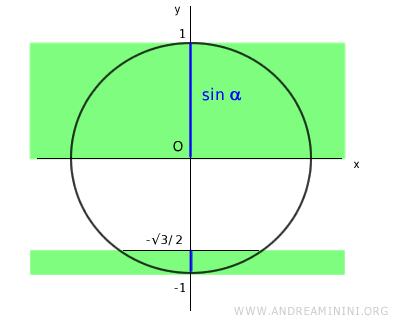
• La funzione sin x ha un valore compreso tra -1 e -√3/2 nell'intervallo $$ x \in [ \pi + \frac{\pi}{3} \ , \ 2 \pi - \frac{\pi}{3} ] $$ $$ x \in [ \frac{3 \pi + \pi}{3} \ , \ \frac{ 6 \pi - \pi}{3} ] $$ $$ x \in [ \frac{4}{3} \pi \ , \ \frac{5}{3} \pi ] $$
• La funzione sin x ha un valore compreso tra 0 e 1 nell'intervallo $$ x \in [ 0 \ , \ \pi ] $$

Pertanto, in un angolo giro (0, 2π) la disequazione è soddisfatta quando la x assume i seguenti angoli

$$ \frac{4}{3} \pi \le x \le \frac{5}{3} \pi \ \ ∨ \ \ 0 \le x \le \pi $$

Poiché il seno è una funzione periodica, devo considerare anche le soluzioni periodiche aggiungendo 2kπ

$$ \frac{4}{3} \pi + 2k \pi \le x \le \frac{5}{3} \pi + 2k \pi \ \ ∨ \ \ 0 + 2k \pi \le x \le \pi + 2k \pi $$

Dove k è un numero intero qualsiasi.

Il grafico della funzione goniometrica conferma il risultato

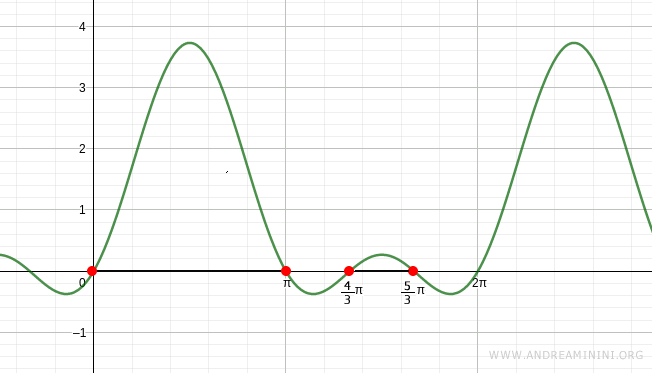
E così via.