Il valore delle funzioni trigonometriche di 60° (π/3)

Un angolo π/3 radianti (pi greco terzi) equivale a un angolo di 60° gradi.

Quanto vale il seno e il coseno di π/3 radianti? Quanto la tangente e la cotangente?

Provo a calcolare il valore delle funzioni trigonometriche di un angolo π/3 facendo alcune considerazioni geometriche.

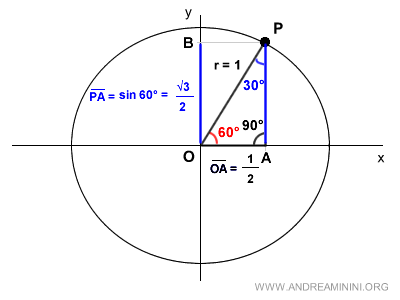
La circonferenza goniometrica ha un raggio pari a uno r=1.

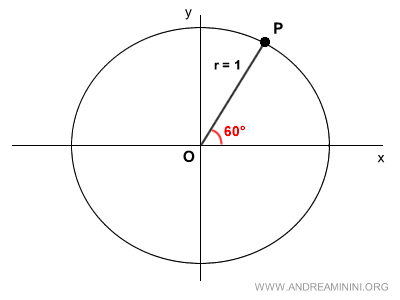
Traccio un segmento OP con un angolo orientato di π/3 radianti rispetto all'asse delle ascisse.

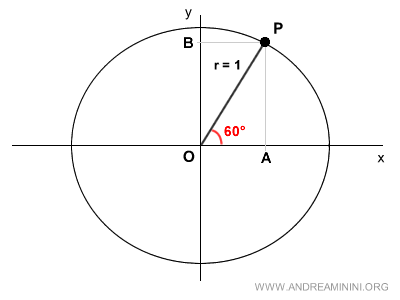
Proietto le coordinate del punto P sull'asse delle ordinate (y) e delle ascisse (x).

Ottengo due punti A e B sugli assi cartesiani.

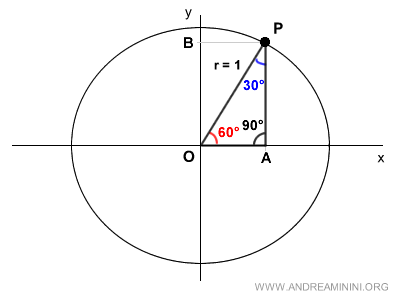
Unisco i punti OPA e ottengo un triangolo rettangolo composto da un angolo retto π/2 (90°) e due angoli complementari pari a π/3 rad (60°) e π/6 rad (30°).

Ora considero il punto di origine C sull'asse orizzontale.

Traccio un segmento PC e ottengo un altro rettangolo OPC con gli stessi angoli del precedente, un angolo retto π/2 (90°) e due angoli complementari pari a π/3 rad (60°) e π/6 rad (30°).

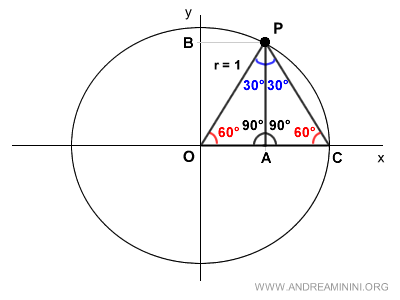
Traccio dei segmenti tra i punti OPC e ottengo un rettangolo con tutti gli angoli uguali a π/3 rad (60°).

Pertanto, i lati del triangolo OPC sono lati congruenti e hanno la stessa lunghezza OP=OC=PC.

La lunghezza del segmento OP coincide con il raggio r=1. Quindi tutti i lati sono pari a uno OP=OC=PC = 1

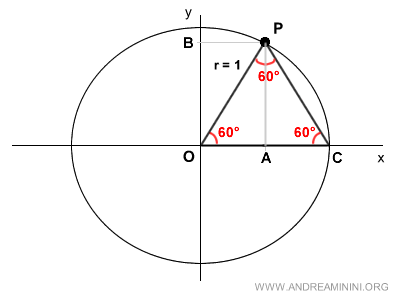
Il segmento OA è esattamente la metà del segmento OC = 1.

$$ \overline{OA} = \frac{1}{2} \cdot \overline{OC} $$

$$ \overline{OA} = \frac{1}{2} \cdot 1 $$

$$ \overline{OA} = \frac{1}{2} $$

Ho trovato la lunghezza del segmento OA che coincide con il coseno di 60° (π/3).

 

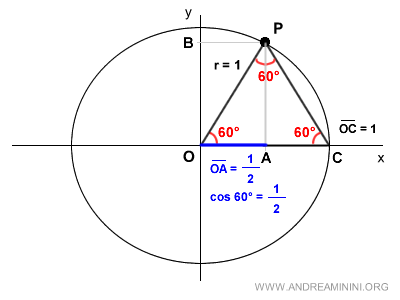
Ho così trovato il coseno dell'angolo π/3.

$$ \cos \frac{π}{3} = \frac{1}{2} $$

Riprendo il triangolo rettangolo iniziale OPA.

Ora conosco sia l'ipotenusa OP=1 e sia il coseno OA=1/2.

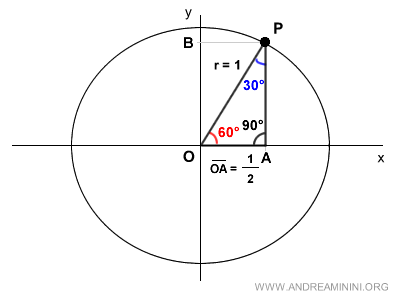
Applico il teorema di Pitagora per calcolare la lunghezza del segmento PA.

$$ \overline{PA} = \sqrt{ \overline{OP}^2 - \overline{OA}^2 } $$

$$ \overline{PA} = \sqrt{ 1^2 - (\frac{1}{2})^2 } $$

$$ \overline{PA} = \sqrt{ 1 - \frac{1}{4} } $$

$$ \overline{PA} = \sqrt{ \frac{4-1}{4} } $$

$$ \overline{PA} = \sqrt{ \frac{3}{4} } $$

$$ \overline{PA} = \frac{\sqrt{ 3 }}{2} $$

Ho trovato anche la lunghezza del lato PA ossia del seno di 60° (π/4).

Quindi il seno dell'angolo π/3 è

$$ \sin \frac{π}{3} = \frac{\sqrt{3}}{2} $$

Una volta noti i valori del seno e del coseno calcolo la tangente di π/3.

$$ \tan \frac{π}{3} = \frac{ \sin \frac{π}{3} }{ \cos \frac{π}{3} } $$

$$ \tan \frac{π}{3} = \frac{ \frac{\sqrt{3}}{2} }{ \frac{1}{2} } $$

$$ \tan \frac{π}{3} = \frac{\sqrt{3}}{2} \cdot 2 $$

$$ \tan \frac{π}{3} = \sqrt{3} $$

Poi calcolo la cotangente di π/3.

$$ cotg \ \frac{π}{3} = \frac{ \cos \frac{π}{3} }{ \sin \frac{π}{3} } $$

$$ cotg \ \frac{π}{3} = \frac{ \frac{1}{2} }{ \frac{\sqrt{3}}{2} } $$

$$ cotg \ \frac{π}{3} = \frac{1}{2} \cdot \frac{2}{\sqrt{3}} $$

$$ cotg \ \frac{π}{3} = \frac{1}{\sqrt{3}} $$

Moltiplico e divido il secondo membro per la radice di 3

$$ cotg \ \frac{π}{3} = \frac{1}{\sqrt{3}} \cdot \frac{ \sqrt{3} }{ \sqrt{3} } $$

$$ cotg \ \frac{π}{3} = \frac{\sqrt{3}}{3} $$

In questo modo ho calcolato i valori delle funzioni trigonometriche di un angolo di 60° (π/3) con semplici considerazioni geometriche.

E così via.