La sottrazione del coseno
La formula della sottrazione del coseno è $$ \cos(\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta $$
Pertanto, non è mai corretto scrivere
$$ \cos (\alpha - \beta) = \cos \alpha - \cos \beta $$
Un esempio pratico
Il coseno di 90° (π/2) è 0 mentre il coseno di 60° (π/3) è 1/2
$$ \cos \frac{\pi}{2} = 0 $$
$$ \cos \frac{\pi}{3} = \frac{1}{2} $$
Devo calcolare il coseno della differenza tra gli angoli 90°-60°
$$ \cos ( \frac{\pi}{2} - \frac{\pi}{3} ) $$
Applico la formula della sottrazione del coseno con α=π/2 e β=π/3
$$ \cos ( \frac{\pi}{2} - \frac{\pi}{3} ) = \cos \frac{\pi}{2} \cos \frac{\pi}{3} + \sin \frac{\pi}{2} \sin \frac{\pi}{3} $$
$$ \cos ( \frac{\pi}{2} - \frac{\pi}{3} ) = 0 \cdot \frac{1}{2} + 1 \cdot\frac{\sqrt{3}}{2} $$
$$ \cos ( \frac{\pi}{2} - \frac{\pi}{3} ) = \frac{\sqrt{3}}{2} $$
Nota. Da notare che $$ \cos ( \frac{\pi}{2} - \frac{\pi}{3} ) \ne \cos ( \frac{\pi}{2} ) - \cos ( \frac{\pi}{3} ) = 0 - \frac{1}{2} $$
Verifica
$$ \cos ( \frac{\pi}{2} - \frac{\pi}{3} ) = \cos ( \frac{3\pi - 2 \pi}{6} ) = \cos ( \frac{\pi}{6}) = \frac{ \sqrt{3} }{2} $$
La dimostrazione
Disegno due angoli α e β in una circonferenza goniometrica con α>β.
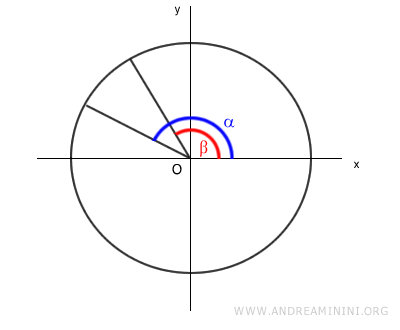
La differenza tra α e β è l'angolo α-β
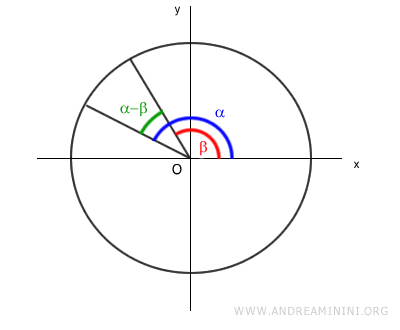
Ora considero lo stesso angolo α-β partire dal lato di origine.
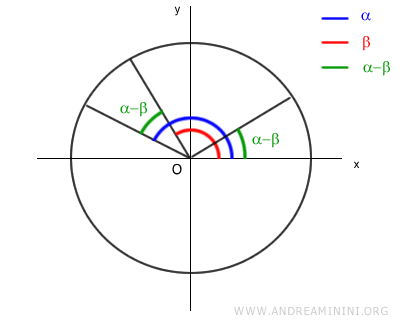
I triangoli OAB e OCD sono congruenti (uguali) perché hanno gli stessi angoli e la stessa lunghezza dei lati.
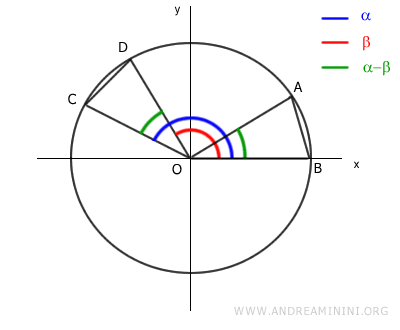
Pertanto i segmenti AB e CD hanno la stessa lunghezza.
$$ \overline{AB} = \overline{CD} $$
Questo vuol dire che la distanza tra i punti A e B è uguale alla distanza tra i punti C e D.
$$ \overline{AB}^2 = (x_A-x_B)^2 +(y_A-y_B)^2 $$
$$ \overline{CD}^2 = (x_C-x_D)^2 +(y_C-y_D)^2 $$
Essendo la stessa distanza
$$ \overline{AB}^2 = \overline{CD}^2 $$
$$ (x_A-x_B)^2 +(y_A-y_B)^2 = (x_C-x_D)^2 +(y_C-y_D)^2 $$
A questo punto devo trasformare le coordinate x e y dei punti con le rispettive funzioni trigonometriche.
Sapendo che xA=cos(α-β) e yA=sin(α-β)
$$ ( \cos(α-β) -x_B)^2 +(\sin(α-β)-y_B)^2 = (x_C-x_D)^2 +(y_C-y_D)^2 $$
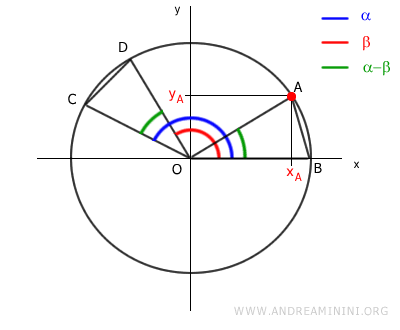
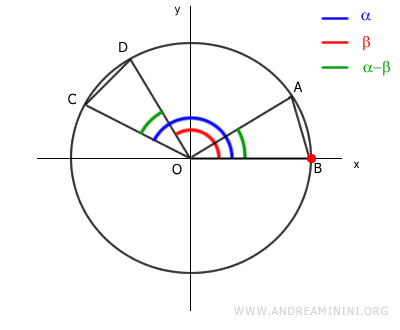
Mentre xB=cos(0)=1 e yB=sin(0)=0.
$$ ( \cos(α-β) -1)^2 +(\sin(α-β)-0)^2 = (x_C-x_D)^2 +(y_C-y_D)^2 $$
$$ ( \cos(α-β) -1)^2 +(\sin(α-β))^2 = (x_C-x_D)^2 +(y_C-y_D)^2 $$
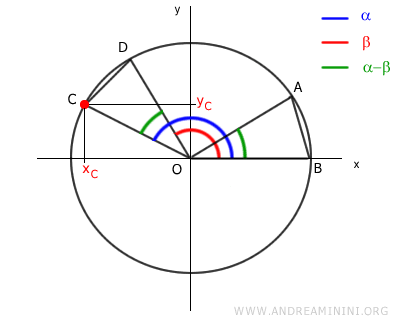
Sapendo che xC=cos(α) e yC=sin(α)
$$ ( \cos(α-β) -1)^2 +(\sin(α-β))^2 = ( \cos(α) -x_D)^2 +( \sin(α) -y_D)^2 $$
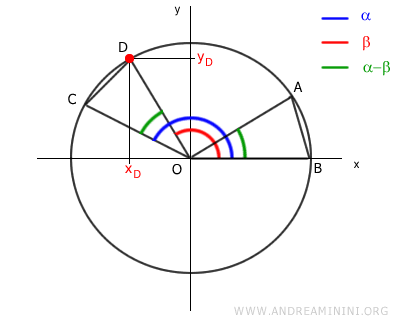
Mentre xD=cos(β) e yD=sin(β)
$$ ( \cos(α-β) -1)^2 +(\sin(α-β))^2 = ( \cos(α) - \cos(β) )^2 +( \sin(α) - \sin(β) )^2 $$
A questo punto semplifico e svolgo i quadrati dei binomi
$$ \cos^2(α-β) - 2 \cos(α-β) +1^2 + \sin^2(α-β) = \cos^2(α) - 2 \cos(α) \cos(β) + \cos^2(β) + \\ + \sin^2(α) - 2 \sin(α) \sin(β) + \sin^2(β) $$
$$ \cos^2(α-β) - 2 \cos(α-β) +1 + \sin^2(α-β) = \cos^2(α) - 2 \cos(α) \cos(β) + \cos^2(β) + \\ + \sin^2(α) - 2 \sin(α) \sin(β) + \sin^2(β) $$
Secondo la prima relazione fondamentale della trigonometria la somma dei quadrati del seno e del coseno di un angolo è uguale a 1.
$$ [ \cos^2(α-β) + \sin^2(α-β) ] - 2 \cos(α-β) +1 = [ \cos^2(α) + \sin^2(α)] - 2 \cos(α) \cos(β) + \\ - 2 \sin(α) \sin(β) + [ \cos^2(β) + \sin^2(β) ] $$
$$ 1 - 2 \cos(α-β) +1 = 1 - 2 \cos(α) \cos(β) - 2 \sin(α) \sin(β) + 1 $$
In questo modo ottengo
$$ 2 - 2 \cos(α-β) = 2 - 2 \cos(α) \cos(β) - 2 \sin(α) \sin(β) $$
Sottraggo 2 in entrambi i membri
$$ 2 - 2 \cos(α-β) \color{red}{- 2} = 2 - 2 \cos(α) \cos(β) - 2 \sin(α) \sin(β) \color{red}{- 2} $$
$$ - 2 \cos(α-β) = - 2 \cos(α) \cos(β) - 2 \sin(α) \sin(β) $$
Poi moltiplico per -1 entrambi i membri per ottenere il segno positivo.
$$ -1 \cdot [ - 2 \cos(α-β) ] = -1 \cdot [ - 2 \cos(α) \cos(β) - 2 \sin(α) \sin(β) ] $$
$$ 2 \cos(α-β) ] = 2 \cos(α) \cos(β) + 2 \sin(α) \sin(β) $$
Ricavo cos(α-β)
$$ \cos(α-β) = \frac{ 2 \cos(α) \cos(β) + 2 \sin(α) \sin(β) }{2} $$
Semplifico il 2 al numeratore e denominatore nel secondo membro e ottengo la formula che volevo dimostrare
$$ \cos(α-β) = \cos(α) \cos(β) + \sin(α) \sin(β) $$
E così via.
