La relazione tra il coefficiente angolare di due rette perpendicolari
Quando due rette sono perpendicolari il coefficiente angolare di una retta è l'opposto del reciproco del coefficiente angolare dell'altra retta. $$ m_1 = - \frac{1}{m_2} $$
Dove m1 è il coefficiente angolare di una retta
$$ r_1: \ \ y=m_1 \cdot x + q $$
ed m2 è il coefficiente angolare dell'altra retta.
$$ r_2: \ \ y=m_2 \cdot x + q $$
Un esempio pratico
Prendo in considerazione due rette
$$ r_1 : \ \ y = -4x +2 $$
$$ r_2 : \ \ y = \frac{1}{4} \cdot x +4 $$
I due coefficienti angolari sono l'opposto del reciproco dell'altro.
$$ m_1 = -4 $$ $$ m_2 = \frac{1}{4} $$
La condizione di ortogonalità è soddisfatta
$$ m_1 = - \frac{1}{m_2} $$
Pertanto, le due rette sono perpendicolari.
Per verificarlo, disegno il grafico con Geogebra e misuro l'angolo di intersezione tra le due rette.
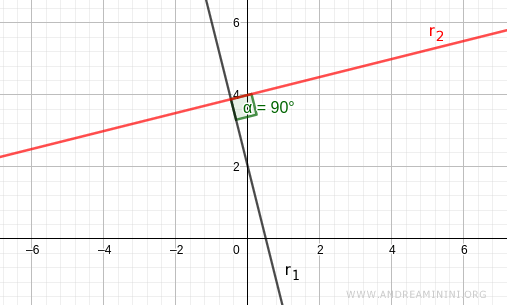
L'angolo di intersezione tra le due rette è effettivamente un angolo retto di 90°.
La dimostrazione
Considero due rette r1 e r2 perpendicolari tra loro che si intersecano nel punto P formando un angolo di 90° (π/2).
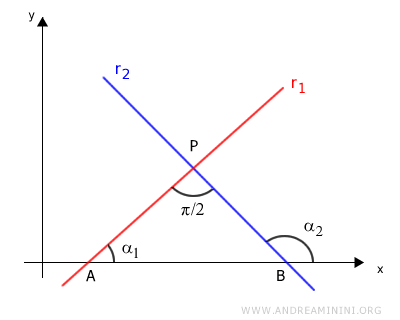
La retta r1 interseca l'asse delle ascisse nel punto A con un angolo α1. Mentrel a retta r2 interseca l'asse delle ascisse nel punto B con un angolo α2.
Unendo i punti A, B, P con dei segmenti ottengo un triangolo rettangolo ABP.
Di questo triangolo conosco l'angolo di intersezione, pari a 90° (π/2), e l'angolo α1.
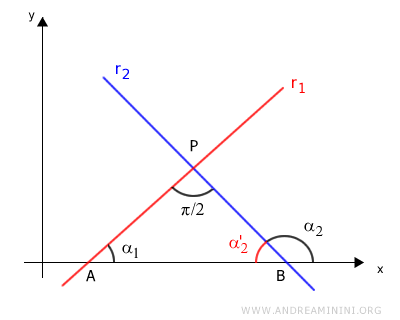
L'angolo α2 è invece un angolo esterno ed è un angolo supplementare rispetto all'angolo interno α2'.
Poiché la somma degli angoli di un triangolo è sempre 180°, l'angolo supplementare α2 è uguale alla somma degli angoli interni non adiacenti
$$ a_2 = \frac{\pi}{2} + a_1 $$
Applico la funzione tangente (tan) a entrambi i membri dell'equazione
$$ \tan a_2 = \tan ( \frac{\pi}{2} + a_1 ) $$
Sapendo che l'angolo associato alla tangente tan(180°+x) è la cotangente -cot(x)
$$ \tan a_2 = -\cot(a_1) $$
Sapendo che la cotangente (cot) è il reciproco della tangente.
$$ \tan a_2 = - \frac{1}{\tan(a_1)} $$
La tangente dell'angolo α2 è il coefficiente angolare m2 di una retta tan α2=m2
$$ m_2 = - \frac{1}{\tan(a_1)} $$
La tangente dell'angolo α1 è il coefficiente angolare m1 dell'altra retta tan α1=m1
$$ m_2 = - \frac{1}{m_2} $$
E in questo modo trovo la formula che volevo dimostrare.
E così via.
