Come calcolare angoli e lati di un triangolo con la trigonometria

Per risolvere un triangolo con la trigonometria, devo conoscere almeno


• un lato e due angoli
• due lati e l'angolo tra i lati (o opposto a uno dei due lati)
• tre lati

La risoluzione di un triangolo consiste nel trovare la lunghezza dei lati e l'ampiezza degli angoli.

Un esempio pratico

A seconda dei dati iniziali posso seguire diverse strade

Esempio 1

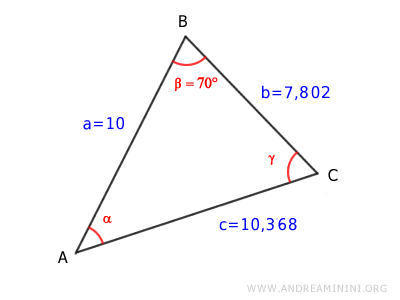
In questo esempio conosco la lunghezza di un lato e l'ampiezza di due angoli del triangolo

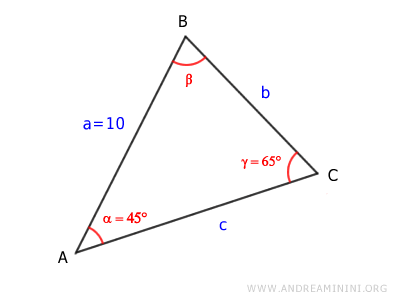
La lunghezza del lato è

$$ \overline{AB} = 10 $$

Gli angoli conosciuti sono

$$ \alpha = 45° $$

$$ \gamma = 65° $$

Sapendo che la somma degli angoli di un triangolo è sempre pari a 180° (p radianti)

$$ \alpha + \beta + \gamma = 180° $$

Trovo l'ampiezza dell'angolo mancante per differenza, poiché conosco gli angoli α=45° e γ=65°.

$$ \beta = 180° - \alpha - \gamma $$

$$ \beta = 180° - 45° - 65° $$

$$ \beta = 70° $$

L'ampiezza dell'angolo mancante è β=70°

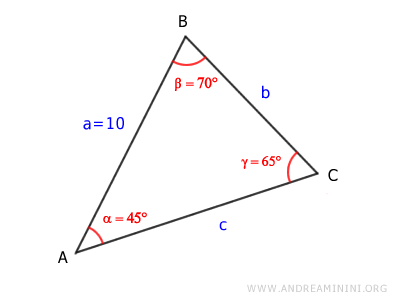
A questo punto posso determinare la lunghezza dei lati usando il teorema dei seni, in base al quale ogni lato di un triangolo è proporzionale al seno dell'angolo opposto.

$$ \frac{\overline{AB}}{\sin \gamma} = \frac{\overline{BC}}{\sin \alpha} = \frac{\overline{AC}}{\sin \beta} $$

Calcolo la lunghezza del lato BC sapendo che AB = 10, γ=65° e α=45°

$$ \frac{\overline{AB}}{\sin \gamma} = \frac{\overline{BC}}{\sin \alpha} $$

$$ \frac{10}{\sin 65°} = \frac{\overline{BC}}{\sin 45°} $$

$$ \overline{BC} = \frac{10}{\sin 65°} \cdot \sin 45°$$

$$ \overline{BC} = 7,802 $$

Calcolo la lunghezza del lato AC sapendo che AB = 10, γ=65° e β=70°

$$ \frac{\overline{AB}}{\sin \gamma} = \frac{\overline{AC}}{\sin \beta} $$

$$ \frac{10}{\sin 65°} = \frac{\overline{AC}}{\sin 70°} $$

$$ \overline{AC} = \frac{10}{\sin 65°} \cdot \sin 70° $$

$$ \overline{AC} = 10,368 $$

Quindi le lunghezze dei lati mancanti sono BC=7,802 e AC=10,368

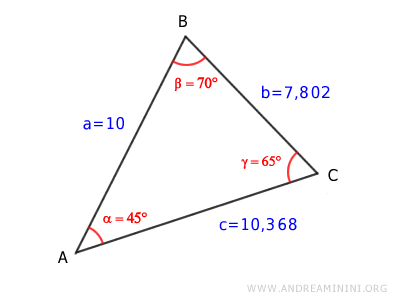
Il triangolo è risolto poiché conosco l'ampiezza di tutti gli angoli e la lunghezza di tutti i lati.

Esempio 2

In quest'altro esempio conosco la lunghezza di due lati e dell'angolo compreso tra i due lati.

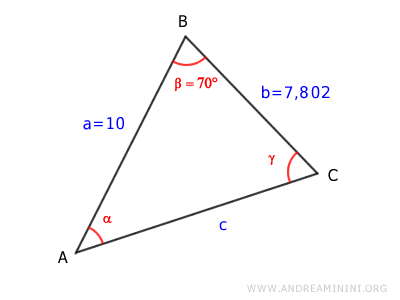
La lunghezza dei lati è

$$ \overline{AB} = 10 $$

$$ \overline{BC} = 7,802 $$

L'angolo compreso tra i due lati è

$$ \beta = 70° $$

In questo caso posso applicare il teorema del coseno, in base al quale il quadrato di un lato AC² è uguale alla somma dei quadrati degli altri due lati AB²+BC² meno il doppio prodotto 2·AB·BC per il coseno dell'angolo compreso (β) tra AB e BC.

$$ \overline{AC}^2 = \overline{AB}^2 + \overline{BC}^2 -2 \overline{AB} \cdot \overline{BC} \cdot \cos \beta $$

Sapendo che l'angolo β=70° e la lunghezza dei lati noti è AB=10 e AC=7,8

$$ \overline{AC}^2 = 10^2 + 7,802^2 -2 \cdot 10 \cdot 7,802 \cdot \cos 70° $$

$$ \overline{AC}^2 = 100 + 60,871 - 2 \cdot 78,02 \cdot \cos 70° $$

$$ \overline{AC}^2 = 160,84 - 156,04 \cdot \cos 70° $$

$$ \overline{AC}^2 = 107,502 $$

Calcolo la radice quadrata a entrambi i membri dell'equazione

$$ \sqrt{ \overline{AC}^2 } = \sqrt{ 107,502 } $$

$$ \overline{AC} = 10,368 $$

In questo modo ottengo la lunghezza del lato mancante AC=10,368.

A questo punto, note le lunghezze dei lati del triangolo uso di nuovo il teorema del coseno per calcolare gli angoli mancanti alfa e gamma.

$$ \overline{AB}^2 = \overline{BC}^2 + \overline{AC}^2 -2 \overline{BC} \cdot \overline{AC} \cdot \cos \gamma $$

Metto in evidenza il coseno di gamma.

$$ \overline{AB}^2 - \overline{BC}^2 - \overline{AC}^2 = -2 \cdot \overline{BC} \cdot \overline{AC} \cdot \cos \gamma $$

$$ \overline{BC}^2 + \overline{AC}^2 - \overline{AB}^2= 2 \cdot \overline{BC} \cdot \overline{AC} \cdot \cos \gamma $$

$$ \cos \gamma = \frac{ \overline{BC}^2 + \overline{AC}^2 - \overline{AB}^2 }{ 2 \cdot \overline{BC} \cdot \overline{AC} } $$

$$ \cos \gamma = \frac{ 7,802^2 + 10,368^2 - 10^2 }{ 2 \cdot 7,802 \cdot 10,368 } $$

$$ \cos \gamma = 0,4226 $$

Applico l'arcocoseno a entrambi i membri e ottengo l'ampiezza dell'angolo gamma.

$$ \arccos( \cos \gamma ) = \arccos(0,4226) $$

$$ \gamma = 65° $$

Sapendo che la somma degli angoli di un triangolo è 180°

$$ \alpha + \beta + \gamma = 180° $$

Una volta noti gli angoli gamma e beta, ottengo l'angolo alfa per differenza

$$ \alpha = 180° - \beta - \gamma $$

$$ \alpha = 180° - 70° - 65° $$

$$ \alpha = 45° $$

Ora conosco tutti gli angoli e i lati del triangolo.

Nota. In alternativa per calcolare l'angolo gamma potrei anche utilizzare il teorema del seno. $$ \frac{\overline{AB}}{\sin \gamma} = \frac{\overline{BC}}{\sin \alpha} = \frac{\overline{AC}}{\sin \beta} $$ In questo caso conosco l'angolo β=70°, quindi lo utilizzo per calcolare uno degli altri due angoli. Ad esempio l'angolo gamma. $$ \frac{\overline{AB}}{\sin \gamma} = \frac{\overline{AC}}{\sin \beta} $$ $$ \frac{10}{\sin \gamma} = \frac{10,368}{\sin 70°} $$ $$ \sin \gamma = \frac{10 \cdot \sin 70° }{ 10,368} = 0,91 $$ $$ \sin \gamma = 0,91 $$ Applico l'arcoseno a entrambi i membri dell'equazione per calcolare l'angolo gamma $$ \arcsin(\sin \gamma) = \arcsin(0,91) $$ $$ \gamma = 65° $$ Tuttavia, in questo caso non conviene usare il teorema del seno. Perché per ogni valore k del seno sin(α)=k ci sono due angoli tra cui scegliere. E' meglio usare il coseno perché per ogni valore k del coseno cos(α)=k c'è un solo angolo perché l'altro angolo che determina il valore k è opposto al primo.

Esempio 3

In quest'altro esempio conosco la lunghezza di due lati e dell'angolo opposto a uno dei due lati.

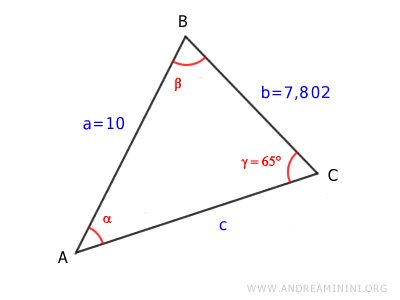
La lunghezza dei lati è

$$ \overline{AB} = 10 $$

$$ \overline{BC} = 7,802 $$

L'angolo gamma γ è l'angolo opposto al lato AB

$$ \gamma = 65° $$

Per risolvere il problema uso il teorema del seno.

$$ \frac{\overline{AB}}{\sin \gamma} = \frac{\overline{BC}}{\sin \alpha} = \frac{\overline{AC}}{\sin \beta} $$

$$ \frac{10}{\sin 65°} = \frac{7,802}{\sin \alpha} = \frac{\overline{AC}}{\sin \beta} $$

Per prima cosa calcolo l'angolo α

$$ \frac{10}{\sin 65°} = \frac{7,802}{\sin \alpha} $$

$$ \sin \alpha = \frac{7,802}{10} \cdot \sin 65°$$

$$ \sin \alpha = 0,7071 $$

Poi applico l'arcoseno a entrambi i membri dell'equazione

$$ \arcsin ( \sin \alpha ) = \arcsin ( 0,7071 ) $$

$$ \sin \alpha = 45° $$

Il risultato è l'angolo α=45°

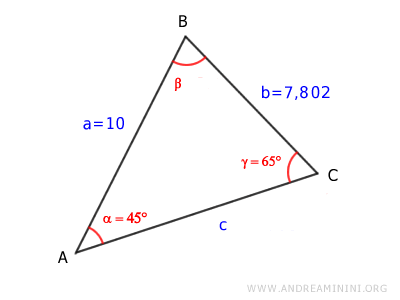
Nota. Devo comunque ricordarmi che il teorema del seno non sempre è utilizzabile. In questo caso mi permette di calcolare un angolo minore di 90° poiché il valore del seno è compreso tra 0 e 1.

Una volta noti due angoli del triangolo, calcolo l'angolo restante per differenza sapendo che la somma degli angoli è sempre pari a 180°.

$$ \alpha + \beta + \gamma = 180° $$

$$ \beta = 180° - \alpha - \gamma $$

$$ \beta = 180° - 45° - 65° $$

$$ \beta = 70° $$

Ora conosco tutti gli angoli del triangolo.

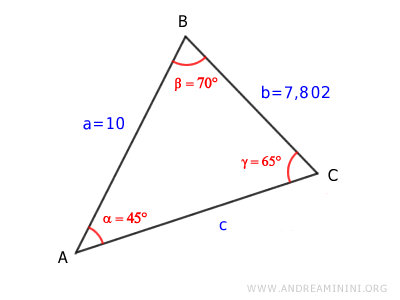
Per calcolare la lunghezza del lato AC utilizzo il teorema del coseno.

$$ \overline{AC}^2 = \overline{AB}^2 + \overline{BC}^2 -2 \overline{AB} \cdot \overline{BC} \cdot \cos \beta $$

$$ \overline{AC}^2 = 10^2 + 7.802^2 -2 \cdot 10 \cdot 7.802 \cdot \cos 70° $$

$$ \overline{AC}^2 = 100 + 60,871 - 2 \cdot 78,02 \cdot \cos 70° $$

$$ \overline{AC}^2 = 160,84 - 156,04 \cdot \cos 70° $$

$$ \overline{AC}^2 = 107,502 $$

Calcolo la radice quadrata a entrambi i membri dell'equazione

$$ \sqrt{ \overline{AC}^2 } = \sqrt{ 107,502 } $$

$$ \overline{AC} = 10,368 $$

Il risultato è la lunghezza del lato mancante AC=10,368 e il triangolo è risolto.

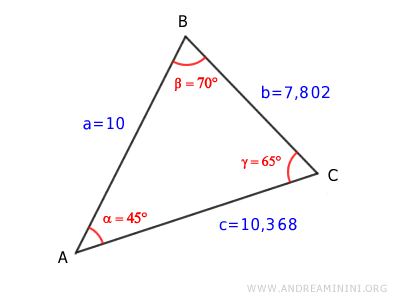
Esempio 4

In questo caso conosco le lunghezze dei lati del triangolo ma non gli angoli.

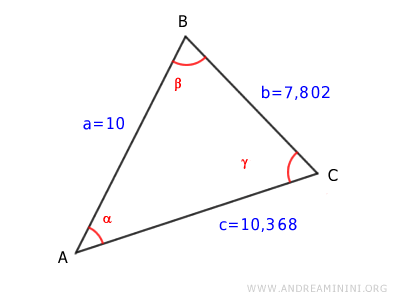
I lati del triangolo sono

$$ \overline{AB} = 10 $$

$$ \overline{BC} = 7,802 $$

$$ \overline{AC} = 10,368 $$

Calcolo l'angolo beta usando il teorema del coseno.

$$ \overline{AC}^2 = \overline{AB}^2 + \overline{BC}^2 -2 \overline{AB} \cdot \overline{BC} \cdot \cos \beta $$

$$ 10,368^2 = 10^2 + 7,802^2 -2 \cdot 10 \cdot 7,802 \cdot \cos \beta $$

$$ 107,495424 = 100 + 60,871204 -156,04 \cdot \cos \beta $$

$$ 107,495424 - 100 - 60,871204 = -156,04 \cdot \cos \beta $$

$$ -53,37578 = -156,04 \cdot \cos \beta $$

Moltiplico per -1 entrambi i membri dell'equazione

$$ 53,37578 = 156,04 \cdot \cos \beta $$

$$ \frac{ 53,37578 }{ 156,04 } = \cos \beta $$

$$ \cos \beta = 0,34206472699 $$

Applico l'arcocoseno a entrambi i membri dell'equazione

$$ \arccos( \cos \beta ) = \arccos(0,34206472699 ) $$

$$ \beta = \arccos(0,34206472699 ) $$

$$ \beta = 70° $$

L'ampiezza dell'angolo beta è β=70°

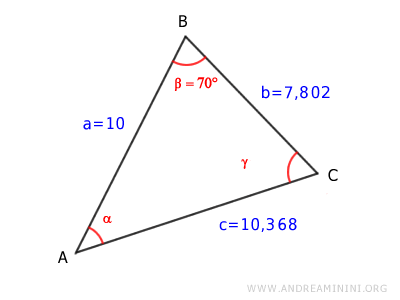
Per calcolare l'angolo alfa utilizzo di nuovo il teorema del coseno.

$$ \overline{BC}^2 = \overline{AB}^2 + \overline{AC}^2 -2 \overline{AB} \cdot \overline{AC} \cdot \cos \alpha $$

$$ 7,802^2 = 10^2 + 10,368^2 -2 \cdot 10 \cdot 10,368 \cdot \cos \alpha $$

$$ 60,871204 = 100 + 107,495424 -207,36 \cdot \cos \alpha $$

$$ 60,871204 - 100 - 107,495424 = -207,36 \cdot \cos \alpha $$

$$ -146,62422 = -207,36 \cdot \cos \alpha $$

Moltiplico per -1 entrambi i membri dell'equazione

$$ 146,62422 = 207,36 \cdot \cos \alpha $$

$$ \frac{146,62422}{207,36} = \cos \alpha $$

$$ \cos \alpha = 0,70709982638 $$

Applico l'arcocoseno a entrambi i membri dell'equazione

$$ \arccos( \cos \alpha ) = \arccos(0,70709982638) $$

$$ \alpha = 45° $$

L'ampiezza dell'angolo alfa è α=45°

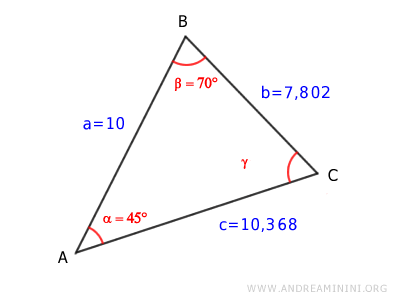
A questo punto è facile calcolare l'angolo gamma per differenza perché la somma degli angoli di un triangolo è sempre 180°.

$$ \alpha + \beta + \gamma = 180° $$

$$ \gamma = 180° - \alpha - \beta $$

$$ \gamma = 180° - 45° - 70° $$

$$ \gamma = 65° $$

L'ampiezza dell'angolo gamma è γ=65°

Ora conosco tutti i lati e gli angoli del triangolo.

Il triangolo è risolto.

E così via.