Come risolvere il triangolo rettangolo con la trigonometria
La risoluzione del triangolo rettangolo consiste nel calcolo della lunghezza dei lati e degli angoli, a partire da alcuni dati noti.
Per risolvere un triangolo rettangolo devo conoscere almeno
- un lato e un angolo acuto
- due lati
In entrambi i casi si utilizza il teorema di Pitagora.
Un esempio pratico
Esistono diversi casi a seconda dei dati iniziali del problema.
Esempio 1
Conosco la lunghezza di due cateti del triangolo rettangolo e devo calcolare tutto il resto.
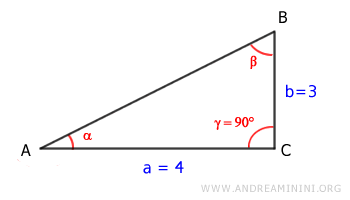
La lunghezza dei lati è
$$ a = 4 $$
$$ b = 3 $$
Applico il teorema di Pitagora per calcolare la lunghezza dell'ipotenusa
$$ c = \sqrt{a^2 + b^2} $$
$$ c = \sqrt{4^2 + 3^2} $$
$$ c = \sqrt{16+9} $$
$$ c = \sqrt{25} $$
$$ c = 5 $$
Quindi, la lunghezza dell'ipotenusa è 5.
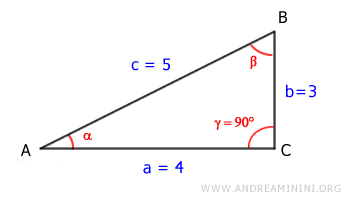
Ora misuro gli angoli.
In base alla seconda relazione fondamentale della trigonometria tan α = sin α / cos α
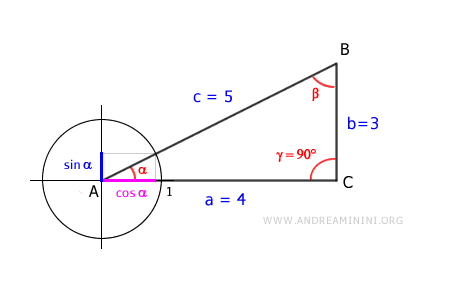
Il rapporto tra sin α / cos α è uguale al rapporto tra i lati b / a perché l'angolo alfa (α) è lo stesso
$$ \sin \alpha : \cos \alpha = b : a $$
Quindi, posso scrivere
$$ \tan \alpha = \frac{\sin \alpha}{\cos \alpha} = \frac{b}{a} $$
Sapendo che la lunghezza dei cateti è b=3 e a=4
$$ \tan \alpha = \frac{3}{4} $$
Applico l'arcotangente a entrambi i membri
$$ \arctan ( \tan \alpha ) = \arctan ( \frac{3}{4} ) $$
Sapendo che l'arcotangente è la funzione inversa della tangente arctan(tan α) = α
$$ \alpha = \arctan ( \frac{3}{4} ) $$
Quindi calcolo l'arcotangente di 3/4
$$ \alpha = \arctan ( \frac{3}{4} ) = 36,87° $$
Nota. Per semplicità in questo esercizio scrivo l'ampiezza degli angoli direttamente in gradi. Bisogna però ricordarsi che spesso la funzione arcotangente delle calcolatrici restituisce l'ampiezza in radianti. In questi casi il risultato dell'arcotangente va convertito da radianti a gradi. E' opportuno ricordarlo se si preferisce lavorare con i gradi.
A questo punto conosco l'angolo α=36,87° e l'angolo γ=90°.
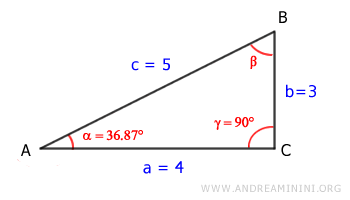
Sapendo che la somma degli angoli di un triangolo è un angolo piatto 180° (ossia π radianti)
$$ \alpha + \beta + \gamma = 180° $$
ottengo l'angolo β del triangolo per differenza
$$ \beta = 180° - \alpha - \gamma $$
$$ \beta = 180° - 36,87° - 90° = 53,13° $$
Pertanto, l'angolo β = 53,13°
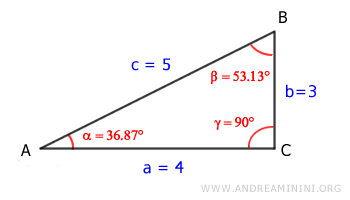
Ho così risolto il triangolo rettangolo.
E' il caso più semplice.
Esempio 2
In questo caso conosco la lunghezza dell'ipotenusa e di un cateto del triangolo rettangolo.
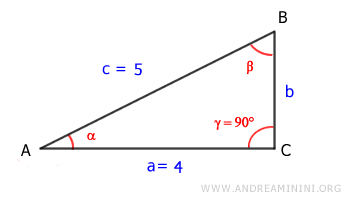
La lunghezza dei lati è
$$ a=4 $$
$$ c=5 $$
Per calcolare la lunghezza dell'altro cateto posso seguire due medodi
Metodo 1
Applico la formula del teorema di Pitagora.
$$ b = \sqrt{c^2 - a^2} $$
Dimostrazione. Sapendo che l'ipotenusa è uguale alla radice della somma dei cateti al quadrato. $$ c = \sqrt{a^2+b^2} $$ Elevo entrambi i lati dell'equazione al quadrato. $$ c^2 = ( \sqrt{a^2+b^2} )^2 $$ $$ c^2 = a^2+b^2 $$ Metto in evidenza il cateto b. $$ c^2 - a^2 = b^2 $$ Quindi, applico la radice quadrata e entrambi i lati dell'equazione. $$ \sqrt{c^2-a^2} = \sqrt{b^2} $$ $$ \sqrt{c^2-a^2} = b $$
Sapendo che c=5 e a=4
$$ b = \sqrt{5^2 - 4^2} $$
$$ b = \sqrt{25 - 16} $$
$$ b = \sqrt{9} = 3 $$
Quindi, la lunghezza dell'altro cateto è b=3.
Una volta note le lunghezze dei lati, gli angoli del triangolo si calcolano come nell'esempio precedente.
Metodo 2
Usando la trigonometria posso calcolare il cateto anche senza applicare il teorema di Pitagora.
In base al primo teorema del triangolo rettangolo
$$ b = c \cdot \sin \alpha $$
$$ b = c \cdot \cos \beta $$
Disegno la circonferenza goniometrica sul vertice A.
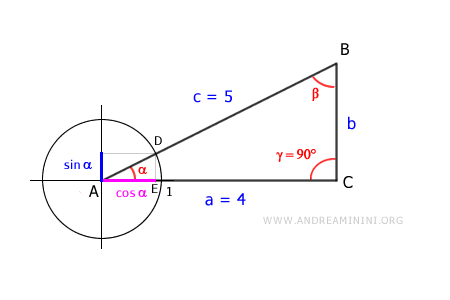
I triangoli ADE e ABC sono simili perché hanno gli stessi angoli.
Quindi, posso scrivere la seguente proporzione.
$$ AE : AD = AC : AB $$
Dove AE è il coseno di alfa
$$ \cos \alpha : AD = AC : AB $$
Il segmento AC è il lato a=4 del triangolo mentre il segmento AB è il lato c=5
$$ \cos \alpha : AD = 4 : 5 $$
Il segmento AD è il raggio unitario della circonferenza goniometrica. Quindi AD=1.
$$ \cos \alpha : 1 = 4 : 5 $$
Pertanto il coseno di alfa è
$$ \cos \alpha = \frac{4}{5} $$
Applico l'arcocoseno a entrambi i membri dell'equazione
$$ \arccos ( \cos \alpha ) = \arccos ( \frac{4}{5} ) $$
$$ \alpha = \arccos ( \frac{4}{5} ) $$
L'arcocoseno di 4/5 è 36,87°
$$ \alpha = 36,87° $$
In questo modo ho trovato l'angolo alfa α = 36,87°.
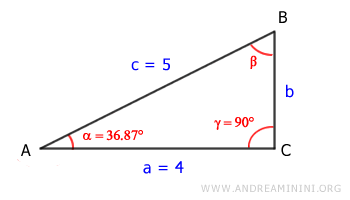
Sapendo che c=5 e α = 36,87° posso calcolare la lunghezza del cateto b tramite il seno dell'angolo opposto α
$$ b = c \cdot \sin \alpha $$
$$ b = 5 \cdot \sin 36,87° $$
$$ b = 3 $$

Nota. In alternativa, una volta noto l'angolo opposto α=36,87°, posso calcolare la lunghezza del cateto b anche usando la formula del coseno dell'angolo adiacente β $$ b = c \cdot \cos \beta $$ Sapendo che la somma degli angoli di un triangolo rettangolo è un angolo piatto, una volta noto l'angolo alfa ottengo per differenza anche l'angolo beta $$ \alpha + \beta + \gamma = 180° $$ $$ \beta = 180° - \alpha - \gamma $$ $$ \beta = 180° - 36,87° - 90° = 53,13° $$ Quindi, la lunghezza del cateto b è $$ b = c \cdot \cos \beta $$ $$ b = 5 \cdot \cos 53,13° = 3 $$ Il procedimento è leggermente più lungo ma il risultato è lo stesso.
Esempio 3
In questo problema conosco la lunghezza di un cateto (b) e un angolo acuto (α) del triangolo rettangolo.
$$ b=3 $$
$$ \alpha = 36.87° $$
Devo calcolare gli altri dati mancanti (angoli e lunghezze) del triangolo rettangolo.
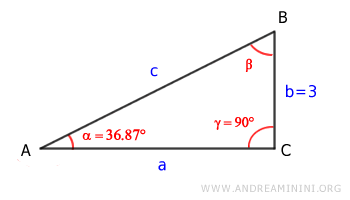
In un triangolo rettangolo la somma degli angoli è uguale a 180°.
$$ \alpha + \beta + \gamma = 180° $$
Poiché ne conosco già due, ottengo l'ampiezza dell'angolo mancante (β) per differenza.
$$ 36.87° + \beta + 90° = 180° $$
$$ \beta = 180° - 36,87° - 90° = 53,13° $$
Ora conosco le ampiezze di tutti gli angoli.
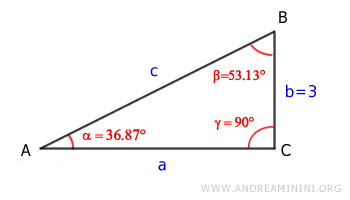
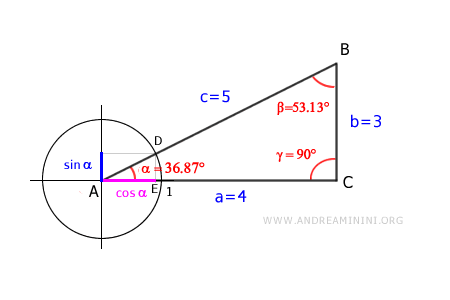
Per calcolare la lunghezza del cateto e dell'ipotenusa disegno la circonferenza goniometrica sul vertice A.
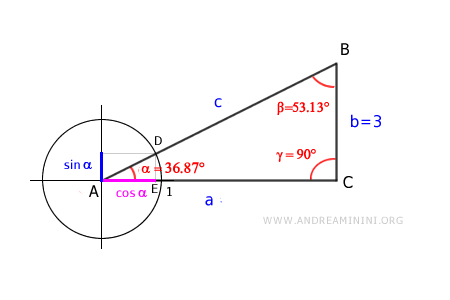
I triangoli ADE e ABC sono triangoli simili perché hanno gli stessi angoli.
Quindi,posso scrivere la proporzione tra il rapporto dei cateti del primo e del secondo.
$$ \overline{AE} : \overline{DE} = \overline{AC} : \overline{BC} $$
Il segmento BC è il lato b del triangolo che già conosco (b=3).
$$ \overline{AE} : \overline{DE} = \overline{AC} : 3 $$
Il segmento AC è il lato a del triangolo.
$$ \overline{AE} : \overline{DE} = a : 3 $$
I segmenti AE e DE sono rispettivamente il coseno e il seno dell'angolo alfa
$$ \cos \alpha : \sin \alpha = a : 3 $$
Riscrivo la proporzione come una frazione
$$ \frac{ \cos \alpha }{ \sin \alpha }= \frac{ a }{ 3 } $$
Poi metto in evidenza il lato a
$$ a = 3 \cdot \frac{ \cos \alpha }{ \sin \alpha } $$
Il rapporto tra il coseno e il seno è la cotangente dell'angolo alfa
$$ a = 3 \cdot \cot \alpha $$
Sapendo che l'angolo alfa è α=36,87°
$$ a = 3 \cdot \cot 36,87° $$
Calcolo il valore della cotangente di 36,87° (cot 36,87° = 1,33) e moltiplico.
$$ a = 3 \cdot 1,33 $$
$$ a = 4 $$
In questo modo ottengo la lunghezza del cateto a=4.
Nota. Se la calcolatrice non ha il tasto della cotangente, posso riscrivere la cotangente come inverso della tangente $$ a = 3 \cdot \frac{ \cos \alpha }{ \sin \alpha } = 3 \cdot \cot \alpha = 3 \cdot \frac{1}{\tan \alpha} = 4 $$ oppure calcolare separatamente il seno e il coseno dell'angolo alfa. Il risultato finale è sempre lo stesso.
Resta da calcolare l'ipotenusa (lato c) del triangolo rettangolo.
Una volta noti i cateti a=4 e b=3, posso calcolare facilmente l'ipotenusa tramite il teorema di Pitagora.
$$ c = \sqrt{a^2+b^2} = \sqrt{4^2+3^2} = \sqrt{16+9} = \sqrt{25} = 5 $$
Tuttavia, in questi appunti penso sia più utile spiegare come calcolare l'ipotenusa usando la trigonometria.
Torno ai triangoli simili ABC e ADE .
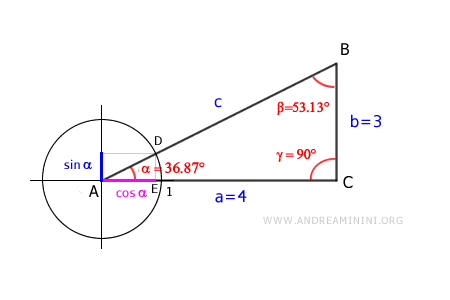
Ora calcolo la proporzione tra l'ipotenusa e un cateto dei due triangoli
$$ \overline{AD} : \overline{AE} = \overline{AB} : \overline{AC} $$
Il segmento AC è il cateto a=4 del triangolo rettangolo
$$ \overline{AD} : \overline{AE} = \overline{AB} : 4 $$
Il segmento AB è l'ipotenusa c del triangolo
$$ \overline{AD} : \overline{AE} = \overline{c} : 4 $$
Il segmento AE è il coseno dell'angolo alfa.
$$ \overline{AD} : \cos \alpha = \overline{c} : 4 $$
Il segmento AD è il raggio unitario della circonferenza goniometrica. Quindi è pari a 1.
$$ 1 : \cos \alpha = \overline{c} : 4 $$
Riscrivo la proporzione come frazione e metto in evidenza l'ipotenusa (c).
$$ \frac{1}{ \cos \alpha } = \frac{ c }{4} $$
$$ c = \frac{4}{ \cos \alpha } $$
L'angolo alfa è α=36,87°
$$ c = \frac{4}{ \cos 36,87° } $$
Il coseno di 36,87° è uguale a 0,8
$$ c = \frac{4}{ 0,8 } $$
$$ c = 5 $$
In questo modo ottengo anche la lunghezza dell'ipotenusa (c=5).
Nota. Fin qui ho fornito ogni volta una spiegazione geometrica e trigonometrica di ogni passaggio. In realtà non è necessario. Per risolvere il triangolo basta ricordarsi le formule del primo teorema del triangolo rettangolo. Nel prossimo esempio sarò molto più sintetico.
Esempio 4
In questo caso conosco la lunghezza dell'ipotenusa e un angolo acuto
$$ c=5 $$
$$ \beta = 53,13° $$
Sapendo che si tratta di un triangolo rettangolo, so anche che c'è un angolo retto γ = 90°
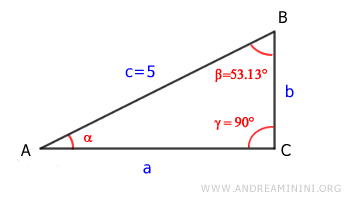
La somma degli angoli di un triangolo è sempre uguale a 180°
$$ \alpha + \beta + \gamma = 180° $$
$$ \alpha + 53,13° + 90° = 180° $$
Questo mi permette facilmente di risalire all'ampiezza dell'angolo alfa per differenza.
$$ \alpha = 180° - 53,13° - 90° = 36,87° $$
A questo punto conosco l'ampiezza di tutti gli angoli.
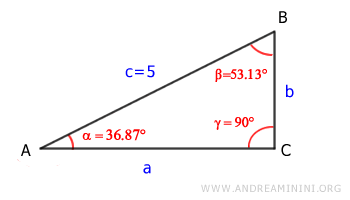
Per calcolare la lunghezza dei cateti utilizzo il primo teorema del triangolo rettangolo.
$$ a = c \cdot \cos \alpha $$
$$ b = c \cdot \sin \alpha $$
In questo caso uso l'angolo alfa per entrambi i cateti.
Calcolo il seno dell'angolo opposto sul cateto b e il coseno dell'angolo adiacente sul cateto a.
Nota. In alternativa, avrei potuto usare l'angolo beta per entrambi o una combinazione diversa. $$ b = c \cdot \cos \beta $$ $$ a = c \cdot \sin \beta $$ Il risultato è sempre lo stesso.
Sapendo che c=5 e α=36,87° ottengo la lunghezza dei cateti
$$ a = 5 \cdot \cos 36,87° = 4 $$
$$ b = 5 \cdot \sin 36,87° = 3 $$
Ora conosco tutte le lunghezze dei lati e le ampiezze degli angoli.
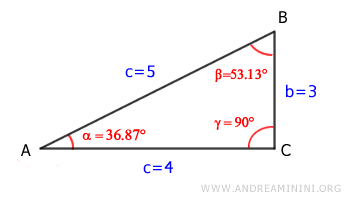
Il triangolo è risolto.
E così via.
