Come calcolare il raggio di una circonferenza circoscritta a un triangolo
Il raggio di una circonferenza circoscritta in un triangolo posso calcolarlo conoscendo un lato del triangolo e l'angolo opposto al lato. $$ r = \frac{ \overline{AB} }{2 \sin \alpha} $$ Dove AB è un cateto e alfa (α) è l'angolo opposto al cateto.
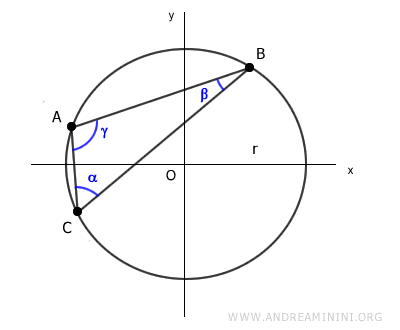
Allo stesso modo posso calcolare il raggio usando uno degli altri lati BC e AC del triangolo con i relativi angoli opposti gamma e beta.
$$ r = \frac{ \overline{BC} }{2 \sin \gamma} $$
$$ r = \frac{ \overline{AC} }{2 \sin \beta} $$
Un esempio pratico
Ho una circonferenza circoscritta a un triangolo ABC
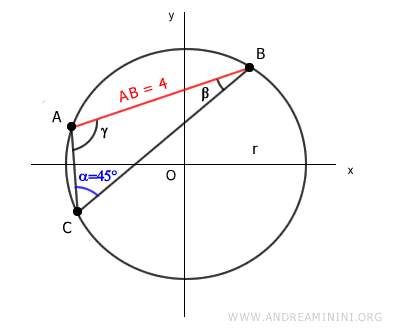
Non conosco il raggio della circonferenza ma conosco la lunghezza del lato AB del triangolo e l'ampiezza dell'angolo opposto α
$$ \overline{AB} = 4 $$
$$ \alpha = 45° $$
Grazie a questi due dati posso calcolare il raggio della circonferenza (r).
$$ r = \frac{ \overline{AB} }{2 \sin \alpha} = \frac{ 4 }{2 \sin 45°} = \frac{ 4 }{2 \frac{\sqrt{2}}{2} } = \frac{ 4 }{\sqrt{2} } = 2,83 $$
Il raggio della circonferenza è 2,83.
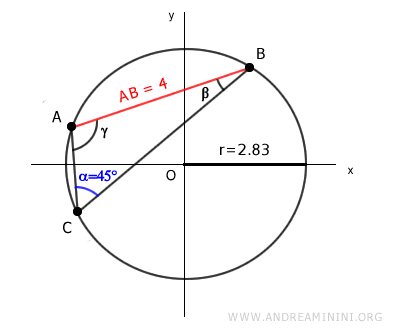
Nota. Allo stesso risultato potevo giungere conoscendo la lunghezza del lato AC e dell'angolo opposto β oppure del lato BC e del lato opposto γ.
La dimostrazione
Prendo in considerazione una circonferenza circoscritta a un triangolo ABC.

Ogni lato del triangolo posso vederlo come una corda.
Ad esempio, il lato AB è una corda che unisce due punti della circonferenza.
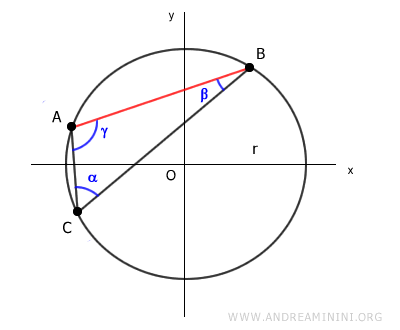
Secondo il teorema della corda la lunghezza della corda AB è uguale al diametro (2r) della circonferenza per il seno dell'angolo opposto (α) al lato AB del triangolo.
$$ \overline{AB} = 2r \cdot \sin \alpha $$
Metto in evidenza il raggio della circonferenza (r) e ottengo la formula che volevo dimostrare.
$$ r = \frac{ \overline{AB} }{2 \sin \alpha} $$
Allo stesso modo si dimostrano le altre formule.
Considero la corda BC
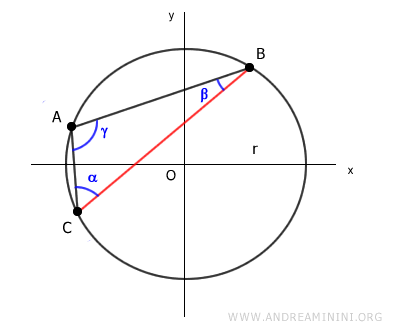
Secondo il teorema della corda, la lunghezza della corda BC è uguale al diametro (2r) della circonferenza per il seno dell'angolo opposto (γ) al lato BC del triangolo
$$ \overline{BC} = 2r \cdot \sin \gamma $$
Metto in evidenza il raggio e ottengo la formula
$$ r = \frac{ \overline{BC} }{2 \sin \gamma} $$
Ora considero la corda AC
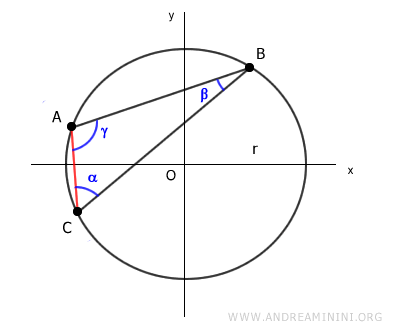
Secondo il teorema della corda, la lunghezza della corda AC è uguale al diametro della circonferena (2r) per il seno dell'angolo opposto (beta)
$$ \overline{AC} = 2r \cdot \sin \beta $$
Metto in evidenza il raggio e ottengo
$$ r = \frac{ \overline{AC} }{2 \sin \beta} $$
E così via.
