I numeri Interi
I numeri interi sono l'insieme dei numeri naturali ( 0, 1, 2, 3, ... ) e dei numeri interi negativi ossia dei numeri naturali con segno meno ( -1, -2, -3, ... ). E' indicato con il simbolo Z. I numeri interi sono anche detti numeri interi relativi.
E' l'insieme di tutte le differenze tra i numeri naturali.
$$ p - q \in Z $$
Dove p e q sono due numeri naturali qualsiasi.
L'insieme dei numeri interi
I numeri interi sono un ampliamento dei numeri naturali.
Per ogni numero naturale diverso da zero esistono due numeri interi, uno con segno più (+) e l'altro con segno meno (-).
Esempio. Al numero naturale 2 sono associati due numeri interi +2 e -2. $
Posso rappresentare i numeri interi su una retta orientata ponendo i numeri in ordine crescente.
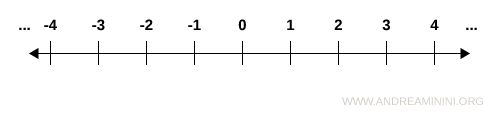
A differenza dei numeri naturali, ogni numero intero z∈Z ha sia un numero precedente z-1 che un numero successivo z+1.
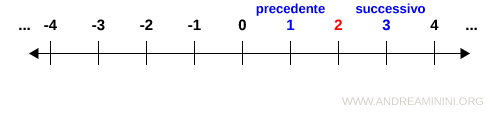
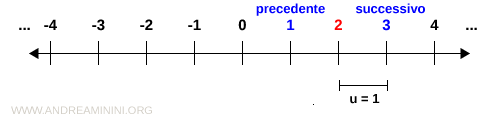
La distanza tra un numero qualsiasi e il suo precedente e il suo successivo è sempre uguale a 1.
Inoltre, tra un numero intero qualsiasi e il suo successivo (o precedente) non esistono altri numeri interi.
L'insieme dei numeri interi si indica usando la lettera maiuscola Z
$$ Z = \{ ... , -3 , -2, -1, 0, 1, 2, 3, ... \} $$
I numeri interi diversi da zero possono appartenere a due sottoinsiemi diversi
- Interi positivi
I numeri interi con segno "+" sono detti numeri interi positivi. L'insieme dei numeri interi positivi è indicato con la lettera Z+. $$ Z^+ = \{1, 2, 3, ... \} $$ Sono tutti i numeri interi maggiori di zero.
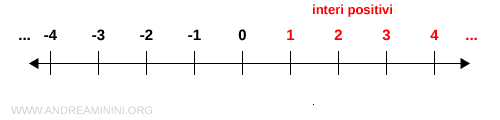
- Interi negativi
I numeri interi con segno "-" sono detti numeri interi negativi. L'insieme dei numeri interi negativi è indicato con la lettera Z-. $$ Z^- = \{... -3, -2, -1 \} $$ Sono tutti i numeri interi minori di zero.
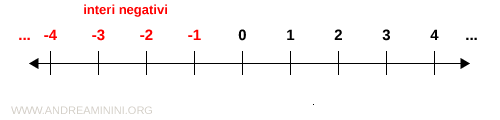
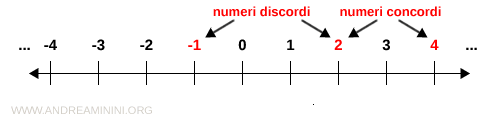
I numeri interi con lo stesso segno sono detti concordi.
Viceversa, i numeri interi con segno diverso sono detti discordi.
Esempio. I numeri interi +2 e +4 sono concordi. I numeri interi +2 e -1 sono invece discordi.
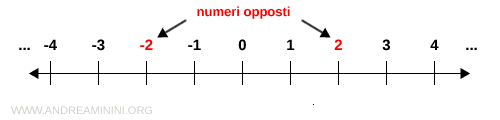
Due numeri interi sono detti opposti se sono discordi e hanno lo stesso valore assoluto.
Per valore assoluto (o modulo) si intende il numero senza considerare il segno.
Esempio. I numeri interi +2 e -2 sono discordi e hanno lo stesso valore assoluto |+2|=2 e |-2|=2. Quindi, +2 e -2 sono numeri opposti.
Qual è il numero opposto di zero? Per chiarire questo concetto è preferibile definire due numeri opposti usando una loro proprietà: "dati due numeri interi opposti la loro somma algebrica è sempre uguale a zero". Ad esempio -2+2=0, -3+3=0, -4+4=0. In questo modo posso dedurre che il numero opposto di zero è se stesso 0+0=0.
In conclusione, l'insieme dei numeri interi ha le seguenti caratteristiche:
- Insieme ordinato
L'insieme dei numeri interi è un insieme ordinato perché dati due numeri interi qualsiasi posso sempre stabilire se un numero è maggiore (minore) dell'altro o sono uguali.Nota. In generale, tra due numeri interi positivi è maggiore il numero che ha il valore assoluto maggiore mentre tra due numeri negativi è maggiore quello che ha il valore assoluto minore. I numeri interi positivi sono sempre maggiori dei numeri interi negativi. Lo zero è maggiore di qualsiasi numero intero negativo e minore di qualsiasi numero intero positivo.
- Insieme infinito
L'insieme dei numeri interi Z è anche un insieme infinito perché è composto da un numero infinito di elementi. - Insieme discreto
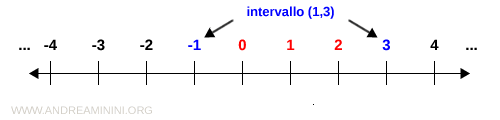
L'insieme dei numeri interi è un insieme discreto perché tra qualsiasi numero intero e il suo numero successivo (o precedente) non esistono altri numeri interi. Quindi, tra due numeri interi qualsiasi (a,b) c'è sempre un numero finito (discreto) di numeri interi.
Esempio. Nell'intervallo compreso tra i numeri interi (-1,3) sono presenti tre numeri interi (0,1,2) ossia un numero finito di elementi.
Le operazioni tra numeri interi
Nell'insieme dei numeri interi sono utilizzabili le seguenti operazioni
- Addizione
$$ a+b = c \ \ \ \ a,b,c \in Z $$ - Sottrazione
$$ a-b = c \ \ \ \ a,b,c \in Z $$ - Moltiplicazione
$$ a \cdot b = c \ \ \ \ a,b,c \in Z $$ - Divisione
$$ a : b = c \ \ \ \ a,b \in Z \ c \in Q $$ - Potenza
$$ a^b = c \ \ \ \ a,b \in Z \ c \in Q $$
Nota. L'addizione, la sottrazione e la moltiplicazione sono operazioni interne all'insieme dei numeri interi Z, perché il risultato è sempre un numero intero. La divisione e la potenza, invece, non sono operazioni interne perché il risultato potrebbe anche non essere un numero intero. Nel caso della divisione e della potenza di due numeri interi il risultato è sempre un numero razionale (Q).
Le proprietà dei numeri interi
I numeri interi soddisfano le seguenti proprietà
- Proprietà commutativa dell'addizione $$ a+b = b+a $$
- Proprietà commutativa della moltiplicazione $$ a \cdot b = b \cdot a $$
- Proprietà associativa dell'addizione $$ (a+b)+c = a+(b+c) $$
- Proprietà associativa della moltiplicazione $$ (a \cdot b) \cdot c = a \cdot (b \cdot c) $$
- Proprietà distributiva della moltiplicazione rispetto all'addizione $$ a (b+c) = ab + ac \\ (a+b)c = ac + bc $$
- Elemento neutro rispetto all'addizione $$ a+0 = 0+a = a $$
- Elemento neutro rispetto alla moltiplicazione $$ a \cdot 1 = 1 \cdot a = a $$
- Elemento opposto $$ a +(- a) = (-a)+a = 0 $$
Dove a,b,c sono tre numeri interi qualsiasi.
Corollari
Dalle precedenti proprietà ne posso derivare altre
-
$$ a \cdot 0 = 0 \cdot a = 0 $$
Dimostrazione
Poiché esiste un elemento neutro dell'addizione 0 $$ a \cdot 0 = a \cdot (0+0) $$ Applico la proprietà distributiva della moltiplicazione $$ a \cdot (0+0) = a \cdot 0 + a \cdot 0 $$ Quindi $$ a \cdot 0 = a \cdot 0 + a \cdot 0 $$ Secondo la proprietà dell'esistenza dell'opposto, la differenza a·0 non può essere che uguale a zero. $$ a \cdot 0 - a \cdot 0 = a \cdot 0 $$ $$ a \cdot 0 - a \cdot 0 = 0 $$ Pertanto $$ a \cdot 0 = 0 $$ -
$$ (-a) \cdot b = -(a \cdot b ) $$
Dimostrazione
Un numero intero b moltiplicato per 0 è uguale a 0. $$ b \cdot 0 = 0 $$ Lo zero può essere sostituito dalla somma di un intero a con il suo opposto -a. $$ b \cdot (a+(-a)) = 0 $$ Applico la proprietà distributiva della moltiplicazione rispetto all'addizione $$ (b \cdot a ) + ( b \cdot (-a)) = 0 $$ Sposto il primo componente a destra dell'equazione e ottengo $$ ( b \cdot (-a)) = - (b \cdot a ) $$Quindi $$ (-a) \cdot b = -(a \cdot b) $$ -
$$ (-a) \cdot (-b) = ab $$
Dimostrazione
Con semplici passaggi algebrici $$ (-a) \cdot (-b) \\ (-1) \cdot a \cdot (-1) \cdot b \\ (-1) \cdot (-1) \cdot a \cdot b $$ Il prodotto (-1)·(-1) è uguale a 1. Quindi ottengo $$ a \cdot b $$
I numeri interi sono un anello commutativo
Le strutture algebriche che soddisfano le stesse proprietà dei numeri interi sono dette anello.
In particolar modo l'insieme dei numeri interi è un anello commutativo unitario o anello commutativo con unità.
Cos'è un anello commutativo?
E' un anello in cui la moltiplicazione è commutativa.
Dati due numeri a e b dell'insieme Z il loro prodotto ab appartiene a Z.
$$ \forall a,b \in Z : a \cdot b = b \cdot a \in Z $$
Esempio
Se prendo dati due numeri interi qualsiasi a e b, anche il loro prodotto è un numero intero.
$$ a \cdot b = b \cdot a \in Z $$
I numeri interi sono un dominio di integrità
Cos'è un dominio di integrità
Un dominio di integrità è un anello commutativo senza divisori dello zero.
Cos'è un divisore dello zero
Un divisore dello zero è un elemento non nullo x di un anello commutativo se esiste un altro elemento non nullo y tale che xy = 0. $$ x \cdot y = 0 $$
Nei numeri interi non c'è un divisore dello zero.
Quindi, i numeri interi sono un dominio di integrità.
Dimostrazione
Devo dimostrare che il prodotto tra numeri interi è uguale a zero se e soltanto se almeno uno dei due fattori è uguale a zero.
$$ a \cdot b = 0 \:\:\: \text{se a=0 ∨ b=0} $$
Se entrambi i fattori sono positivi a>0 e b>0 allora anche il prodotto è maggiore di zero ossia è positivo.
$$ a \cdot b > 0 \:\:\: \text{se a>0 ∧ b>0} $$
Se entrambi i fattori sono negativi a<0 e b<0 il prodotto è maggiore di zero ossia è positivo.
$$ a \cdot b > 0 \:\:\: \text{se a<0 ∧ b<0} $$
Se un fattore è positivo (a>0) e l'altro negativo (b<0) allora l'opposto -b è positivo
$$ a \cdot (-b) > 0 \:\:\: \text{se a>∧ e b<0} $$
Quindi, se -(ab) è positivo allora il prodotto (ab) è negativo
$$ a \cdot b < 0 \:\:\: \text{se a>0 ∧ b<0} $$
Per esclusione deduco che il prodotto ab è uguale a zero se e soltanto se a=0 e/o b=0.
$$ a \cdot b = 0 \:\:\: \text{se a=0 ∨ b=0} $$
Pertanto, nell'insieme dei numeri interi non esiste un divisore dello zero.
Ho così dimostrato che l'insieme dei numeri interi è un dominio di integrità.
Nota. L'assenza di un divisore dello zero non è una caratteristica degli anelli. Il fatto che l'insieme dei numeri interi non abbia un divisore dello zero non esclude che altri anelli lo abbiano. Esistono anche anelli dotati di divisori dello zero. Ad esempio, l'anello Z10 ha divisori dello zero.
E così via.
