Numeri reali
Cosa sono i numeri reali
L'insieme dei numeri reali è l'unione dell'insieme dei numeri razionali (Q) e l'insieme dei irrazionali (I). E' indicato con la lettera R.
L'insieme dei numeri reali include al suo interno l'insieme dei numeri naturali, dei numeri interi, dei numeri razionali ( es. 2/3 ) e irrazionali ( es. √2 ).
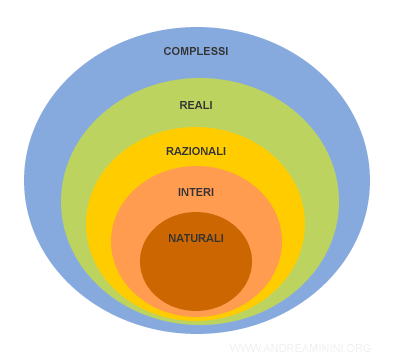
Nota. L'insieme dei numeri razionali (Q) e l'insieme dei numeri irrazionali (I) compongono una partizione dell'insieme dei numeri reali. Sono razionali i numeri esprimibili da una frazione di due numeri interi. Sono irrazionali i numeri non esprimibili da un rapporto di numeri interi.
Le operazioni dei numeri reali
Per ogni coppia di numeri reali a,b sono definite le operazioni
- Addizione (+)
- Moltiplicazione (·)
- Elevazione a potenza (nk)
e le rispettive operazioni inverse
- Sottrazione (-)
- Divisione (/)
- Estrazione di radice (k√n)
Non sono però definite le seguenti operazioni
- La divisione per zero
- La radice con indice pari di un numero negativo
Nota. Le radici con indice pari dei numeri negativi non sono calcolabili con i numeri reali perché nessun numero reale moltiplicato per se stesso un numero pari di volte può avere segno negativo. $$ \sqrt{-2} \ , \ \sqrt[4]{5} \ , \ ... $$ Viceversa, è possibile calcolare con i numeri reali le radici con indice dispari dei numeri negativi. Ad esempio $$ \sqrt[3]{-8} = -2 \ \ perché \ \ (-2) \cdot (-2) \cdot (-2) = -8 $$ Per calcolare anche le radici con indice pari dei numeri negativi devo abbandonare i numeri reali e usare i numeri complessi, un insieme numerico più ampio dei numeri reali.
L'insieme dei numeri reali è un insieme infinito perché è composto da infiniti elementi.
Gli assiomi dei numeri reali
A] Assiomi relativi alle operazioni di addizione e moltiplicazione
- Proprietà associativa $$ (a+b)+c = a+(b+c) $$ $$ (a \cdot b) \cdot c = a \cdot (b \cdot c) $$
Esempio. Dati tre numeri a=2, b=3, c=4. La proprietà associativa rispetto all'addizione $$ (2+3)+4 = 2+(3+4) \\ 5+4 = 2 + 7 \\ 9 = 9 $$ e rispetto alla moltiplicazione $$ (2 \cdot 3) \cdot 4 = 2 \cdot (3 \cdot 4) \\ 6 \cdot 4 = 2 \cdot 12 \\ 24 = 24 $$
- Proprietà commutativa $$ a+b=b+a $$ $$ a \cdot b = b \cdot a $$
Esempio. Dati due numeri a=2, b=3. La proprietà commutativa rispetto all'addizione $$ 2+3 = 3+2 \\ 5=5 $$ e rispetto alla moltiplicazione $$ 2 \cdot 3 = 3 \cdot 2 \\ 6 = 6 $$
- Proprietà distributiva$$ a \cdot (b+c) = a \cdot b + a \cdot c $$
- Elemento neutro
Nell'insieme dei numeri reali esistono due elementi neutri rispettivamente all'operazione di addizione e moltiplicazione. $$ a+0 = a $$ $$ a \cdot 1 = a $$Esempio. $$ 5 + 0 = 5 $$ $$ 5 \cdot 1 = 5 $$
- Elementi opposti
Ogni numero reale (a) ha un numero opposto (-a) tale che la loro somma è l'elemento neutro dell'addizione $$ a+(-a)=0 $$Esempio. $$ 5+(-5)=0 $$ $$ 7 + (-7) = 0 $$
- Elementi inversi
Ogni numero reale (a) diverso da zero ha un numero opposto a-1 tale che il loro prodotto è l'elemento neutro della moltiplicazione ossia 1 $$ a \cdot a^{-1} = 1 $$Esempio. $$ 5 \cdot 5^{-1} = 5 \cdot \frac{1}{5} = 1 $$
Esempio. Dati tre numeri a=2, b=3, c=4. $$ 2 \cdot (3+4) = 2 \cdot 3 + 2 \cdot 4 \\ 2 \cdot 7 = 6 + 8 \\ 14 = 14 $$
B] Assioma dell'ordinamento
Data una coppia di numeri reali a,b esiste una relazione minore-uguale (≤) se la coppia di numeri ha le seguenti proprietà.
- Dati due numeri reali a,b è vera una delle seguenti relazioni: a≤b oppure a≥b. E' detta dicotomia dei numeri reali.
- Dati due numeri reali a,b se valgono entrambe le relazioni a≤b e a≥b allora i due numeri sono uguali a=b. E' detta asimmetria dei numeri reali.
- Se vale la relazione a≤b allora, per qualsiasi numero reale c vale anche la relazione a+c≤b+c
- Se vale la relazione 0≤a e 0≤b allora valgono anche le relazioni 0≤a+b e 0≤a*b.
C] l'Assioma della completezza
Dati due insiemi non vuoti A e B di numeri reali in cui presi due elementi qualsiasi a∈A e b∈B si abbia sempre a≤b, allora esiste un numero reale c tale che a≤c≤b.
La differenza tra numeri reali, interi, naturali e razionali
L'insieme dei numeri reali (R) include dei sottoinsiemi numerici che soddisfano soltanto alcuni assiomi dei numeri reali.
$$ N ⊆ Z ⊆ Q ⊆ R $$
Usando i diagrammi di Venn posso rappresentare gli insiemi numerici in questo modo
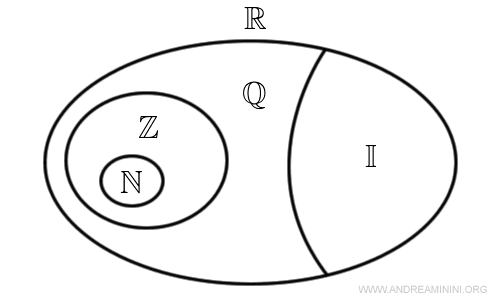
- I numeri naturali (N). L'insieme dei numeri naturali non soddisfa l'assioma dei numeri opposti.
Esempio. Non esiste il numero naturale opposto del numero naturale 5 perché -5 non è un numero naturale.
Si possono svolgere le operazioni di addizione e moltiplicazione ma non sempre le operazioni inverse di sottrazione e divisione. - I numeri interi (Z). L'insieme dei numeri interi non soddisfa l'assioma dei numeri inversi. Soltanto il numero intero 1 soddisfa questa proprietà dei numeri reali.
Esempio. Non esiste il numero intero inverso del numero 7 perché 1/7 ossia 7-1 non è un numero intero.
Nei numeri interi si possono calcolare le operazioni di addizione, moltiplicazione e sottrazione. Non è però possibile in generale effetturare la divisione tra due numeri. - I numeri razionali (Q). L'insieme dei numeri razionali non soddisfa l'assioma di completezza perché non permette sempre di svolgere l'estrazione della radice di un numero.
Esempio. Non esiste nessun numero razionale x=m/n tale che x2 = 2.
I numeri razionali permettono di svolgere sia le operazioni di addizione e moltiplicazione che quelle di sottrazione e divisione. Tuttavia, non soddisfa l'assioma della completezza sul calcolo delle radici dei numeri.
L'insieme dei numeri reali è denso e completo
L'insieme dei numeri reali è un insieme numerico denso e completo
- E' un insieme denso perché dati due numeri reali qualsiasi a e b, è sempre possibile trovare un altro numero reale c compreso tra a e b.
- E' un insieme completo perché a ogni numero reale corrisponde uno e un solo punto della retta. E viceversa.
Pertanto, l'insieme dei numeri reali è in corrispondenza biunivoca con l'insieme dei punti di una retta.
E così via.
