I numeri naturali
Cosa sono i numeri naturali
L'insieme dei numeri naturali sono i numeri usati normalmente per contare o ordinare.
I numeri naturali nascono essenzialmente per contare una quantità di oggetti.
Spesso si indica con N l'insieme dei numeri naturali a partire da 1.
$$ N = \{ 1, 2, 3, 4, ... \} $$
Nota. Il concetto di "zero" nasce molto tempo dopo gli altri. I primi numeri ad essere usati dall'uomo sono 1, 2, 3 ... e via dicendo. Un'unità o due unità sono concetti conosciuti fin dalla preistoria perché sono legati alla realtà materiale. Anche alcuni animali li conoscono. Ad esempio i corvi pare sappiano riconoscere e contare 3-4 oggetti. Lo zero è invece un concetto astratto che indica l'assenza. E' stato introdotto dall'uomo più di recente.
L'insieme dei numeri naturali a partire dallo zero è indicato con N0.
$$ N_0 = N \cup \{ 0 \} = \{ 0, 1, 2, 3, 4, ... \} $$
In ogni caso non esiste una convenzione.
Nota. In alcuni testi di matematica l'insieme N0 è indicato con il simbolo N senza fare alcuna distinzione. A volte l'insieme N0 è anche detto insieme dei numeri interi non negativi.
I numeri naturali sono caratterizzati da un ordine.
Dati due numeri naturali qualsiasi, diversi tra loro, posso sempre stabilire se il primo è minore o maggiore al secondo.
Ogni numero naturale ha un numero successore e numero predecessore.
Esempio. Il numero 7 ha un numero successore 8 $$ 7+1 = 8 $$ e un numero predecessore 6 $$ 7-1=6 $$
Fa eccezione alla regola il primo numero dell'insieme dei numeri naturali, ad esempio lo zero in N0 e l'uno in N, che non ha un predecessore.
La rappresentazione dei numeri naturali
I numeri naturali posso rappresentarli su una semiretta orientata.
Traccio una semiretta a partire da un punto di origine O che coincide con il primo numero naturale (zero o uno a seconda dei casi)
Fisso un verso (freccia) e un'unità di misura (u).

Poi disegno i numeri naturali a partire dal successore di 1 in poi.
Poiché ogni numero naturale ha un successore, ne consegue che esistono infiniti numeri naturali. Pertanto, l'insieme dei numeri naturali è un insieme infinito.
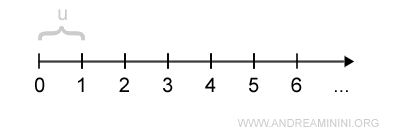
Ogni numero naturale è un punto della semiretta. Tuttavia, non tutti i punti della semiretta sono numeri naturali.
Tra un numero naturale qualsiasi e il suo successore, ad esempio tra 2 e 3, esistono infiniti altri punti della semiretta.
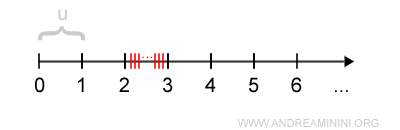
Per questa ragione l'insieme dei numeri naturali è anche detto insieme discreto.
Le operazioni dei numeri naturali
I numeri naturali consentono due operazioni chiuse.
- Addizione
La somma di due numeri naturali è un altro numero naturaleEsempio. La somma dei numeri naturali 5 e 7 è un numero naturale indipendentemente dalla posizione degli addendi. $$ 5+7=7+5=12 \in N $$
- Moltiplicazione
Il prodotto di due numeri naturali è un altro numero naturale.Esempio. Il prodotto dei numeri naturali 5 e 7 è un numero naturale indipendentemente dalla posizione dei fattori. $$ 5 \cdot 7=7 \cdot 5=35 \in N $$
La somma e il prodotto di due numeri naturali è un altro numero naturale. Per questa ragione l'addizione e la moltiplicazione sono dette operazioni interne in N.
Nota. In alternativa, posso anche dire che l'insieme dei numeri naturali è chiuso rispetto all'addizione e alla moltiplicazione. Il significato è sempre lo stesso.
Le operazioni inverse
Le operazioni inverse dell'addizione e della moltiplicazione dei numeri naturali sono rispettivamente la differenza e la divisione.
- Differenza
La differenza tra due numeri naturali a-b, dove a è detto minuendo e b è detto sottraendo, è un numero che addizionato al sottraendo (b) dà come risultato il minuendo (a).Esempio. La differenza dei numeri naturali 7 e 5 è il numero naturale 2. $$ 7-5=2 \in N $$ perché la somma della differenza (2) e del sottraendo (5) dà come risultato il minuendo (5) $$ 2+5=7 $$
- Divisione
La divisione tra due numeri naturali a:b, dove a è detto dividendo e b è detto divisore, è un numero detto quoziente (q) che moltiplicato per il divisore (b) dà come risultato il dividendo (a).
Esempio. La divisione tra 8 e 2 è il numero naturale 4. $$ 8:2=4 \in N $$ perché il prodotto tra il quoziente (4) e il divisore (2) dà come risultato il dividendo (8) $$ 4 \cdot 2 = 8 $$
L'insieme dei numeri naturali non è chiuso rispetto alla sottrazione e alla divisione.
La sottrazione non è un'operazione interna in N perché non è detto che la differenza sia sempre un numero naturale.
Esempio. La differenza dei numeri naturali 5 e 7 dà come risultato il numero -2 che non è un numero naturale. $$ 5-7 = -2 $$ Non è un'operazione interna in N perché non esiste un numero naturale n∈N tale che $$ n+7=5 $$
In particolar modo nei numeri naturali la sottrazione è possibile solo quando il minuendo è maggiore o uguale al sottraendo.
$$ \text{minuendo } \ \ge \ \text{sottraendo} $$
Esempio. La differenza tra 7 e 5 è un numero naturale. $$ 7-5 = 2 \in N $$ La differenza tra 5 e 7, invece, non è un numero naturale $$ 5-7=-2 \notin N $$
Per rendere interna la sottrazione devo introdurre un altro insieme numerico: l'insieme dei numeri interi (Z).
La divisione non è un'operazione interna nell'insieme dei numeri naturali per due motivi
- La divisione per zero è impossibile perché se un numero naturale n fosse divisibile per 0 allora esisterebbe un altro numero naturale q tale che q·0=n. Tuttavia, qualsiasi numero moltiplicato per zero è sempre uguale a zero. Quindi, l'operazione è indeterminata.
$$ \text{divisore} \ \ne \ 0 $$ - La divisione di un numero naturale (dividendo) per un altro numero naturale (divisore) diverso da zero, non è detto che dia come risultato un numero naturale.
Esempio. La divisione tra due i numeri naturali $$ 5:2=q $$ non dà come risultato un numero naturale perché non esiste un numero naturale q in N tale che $$ q \cdot 2=5 $$ In questo caso il quoziente tra 5:2 è il numero reale 2.5 $$ 5:2=2.5 $$
La divisione tra due numeri naturali è possibile solo se la divisione è esatta, ossia se anche il quoziente è un numero naturale.
Nota. In alternativa, la divisione tra due numeri naturali è possibile se al quoziente si aggiunge il concetto di resto (detta divisione non esatta). $$ \text{dividendo = divisore · quoziente (q) + resto (r)} $$ Ad esempio, la divisione tra due i numeri naturali $$ 5:2=q+r $$ restituisce un quoziente q=2 con resto pari a r=1. $$ 2 \cdot 2 + 1 =1 $$
Gli assiomi dei numeri naturali
L'insieme dei numeri naturali è definito dai seguenti assiomi
- L'insieme dei numeri naturali è chiuso rispetto alla somma e al prodotto
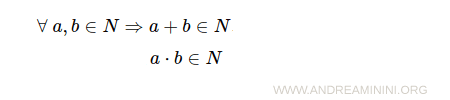
- Proprietà commutativa della somma e del prodotto
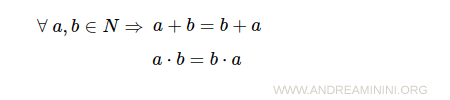
- Proprietà associativa della somma e del prodotto
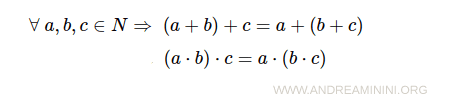
- Proprietà distributiva della somma e del prodotto
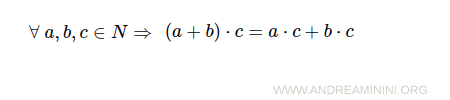
- Esistenza di un elemento neutro rispetto al prodotto
L'elemento neutro rispetto al prodotto è il numero 1. Se moltiplico un numero naturale qualsiasi a∈N per 1, il prodotto è il numero stesso.
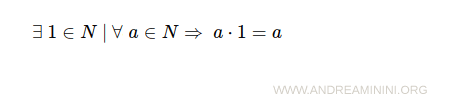
L'elemento neutro rispetto al prodotto è unico. Vedi dimostrazione unicità elemento neutroNota. Nel caso dell'insieme dei numeri naturali N0 che include anche lo zero $$ N_0 = N \cup \{ 0 \} = \{ 0, 1, 2, 3, 4, ... \} $$ devo considerare anche l'elemento neutro rispetto all'addizione anche conosciuto come sesto assioma dei numeri interi non negativi. Per ogni numero n che appartiene all'insieme dei numeri naturali N, la somma n+0 oppure 0+n è uguale a n $$ \forall n \ \in N \Rightarrow \ n+0=0+n=n $$ Inoltre, nel caso specifico dei numeri naturali la somma è uguale a zero solo se entrambi gli addendi sono zero $$ 0 + 0 = 0 $$ Lo zero è anche l'elemento assorbente della moltiplicazione da cui deriva la legge di annullamento del prodotto. Il prodotto tra un numero naturale qualsiasi per zero è sempre nullo. Ad esempio $$ 3 \cdot 0 = 0 \cdot 3 = 0 $$
Questi cinque assiomi mi permettono di definire l'insieme dei numeri naturali.
Un modo alternativo per definire i numeri naturali sono gli assiomi di Peano.
Elemento successivo
Preso un numero qualsiasi a di N0, l'elemento successivo (successore) di a è l'elemento a+1 $$ \forall \ a \in N_0 \rightarrow a+1 \in N_0 $$
La definizione di elemento successivo deriva dal sesto assioma dei numeri interi non negativi N0
Poiché ogni numero ha un elemento successivo, questo dimostra che l'insieme dei numeri naturali contiene infiniti numeri.
Gli assiomi di Peano
Il matematico Giuseppe Peano definisce l'insieme dei numeri naturali con alcuni assiomi, detti assiomi di Peano
- Esiste un numero naturale 0.
- Ogni numero naturale ha un numero successivo $$ σ(n)=n+1 $$
- Non esiste un numero naturale con successore zero $$ σ(n)≠0 $$
- Numeri naturali distinti hanno successori distinti $$ σ(a)≠σ(b) $$
- Ogni sottoinsieme U di N che contiene lo zero e il successore di ogni elemento coincide con l'insieme dei numeri naturali. $$ \begin{cases} 0 \in U \\ \\ \forall k \in U \Rightarrow σ(k) \in U \end{cases} $$ Questo postulato è detto principio di induzione matematica oppure effetto domino.
Quindi, secondo gli assiomi di Peano, l'insieme dei numeri naturali è composto da un insieme di numeri, un'applicazione σ e lo zero.
$$ \{ N,σ,0 \} $$
L'applicazione σ è iniettiva perché a ogni numero naturale n associa un numero successore n+1.
$$ \forall n \in N \rightarrow s(n) = n+1 $$
L'elemento 0 non appartiene all'insieme delle immagini dell'applicazione σ perché per definizione non è successore a nessun numero naturale.
Nota. Essendo postulati vanno accettati senza alcuna dimostrazione.
Il principio del minimo
Il principio del minimo ( o del buon ordinamento ) è un'altra proprietà fondamentale dei numeri naturali
Ogni sottoinsieme M dei numeri naturali N ha un minimo
Dato un sottoinsieme T non vuoto di N, esiste un elemento m di T tale che m ≤ t per ogni t di T.
$$ \forall t \in T \:\: \exists \:\: m \in T \:\:|\:\: m \le t $$
Esempio
Nel sottoinsieme T1 di N l'elemento minimo è lo zero.
$$ T_1 = \{ n \in N \:\:|\:\: n \le 5 \} $$
Nel sottoinsieme T2 di N l'elemento minimo è il numero 2
$$ T_2 = \{ n \in N \:\:|\:\: n \ge 2 \} $$
Nota. Questa proprietà caratterizza soltanto i numeri naturali. Nell'insieme dei numeri interi o reali esistono sottoinsiemi non vuoti privi di un elemento minimo. Ad esempio, Nel sottoinsieme T dei numeri interi inferiori o uguali a 2 non esiste un elemento minimo. $$ T = \{ z \in Z \:\:|\:\: z \le 2 \} $$
L'insieme dei numeri naturali N è detto bene ordinato perché ogni sottoinsieme non vuoto ha un elemento minimo.
E così via.
