Come trasformare e risolvere un'equazione goniometrica in forma elementare

Un'equazione goniometrica composta da più funzioni trigonometriche posso ricondurla a un'equazione goniometrica elementare.

1. Trasformo le funzioni dell'equazione in una stessa funzione trigonometrica di riferimento (ad esempio, il coseno).

   Nota. La scelta della funzione trigonometrica di riferimento dipende dalla convenienza dei calcoli. A volte conviene il coseno, altre il seno o la tangente.

2. Considero la funzione trigonometrica di riferimento come un'incognita
3. Risolvo l'equazione goniometrica e le equazioni goniometriche elementari

Un esempio pratico

Devo risolvere l'equazione goniometrica

$$ 3 \sin^2 x + 4 \cos x = 3 $$

L'equazione è composta dalle funzioni goniometriche seno e coseno.

In questo caso mi conviene usare come funzione di riferimento il coseno.

Secondo la prima relazione fondamentale della trigonometria

$$ \sin^2 x + \cos^2 x =1 $$

Quindi, posso esprimere sin² come coseno

$$ \sin^2 x =1 - \cos^2 x $$

Sostituisco sin² con 1-cos² x nell'equazione goniometrica

$$ 3 \sin^2 x + 4 \cos x = 3 $$

$$ 3 (1-\cos^2 x) + 4 \cos x = 3 $$

$$ 3 - 3 \cos^2 x + 4 \cos x = 3 $$

In questo modo l'equazione goniometrica è espressa solo con la funzione trigonometrica coseno.

Grazie alla proprietà invariantiva trasformo l'equazione goniometrica in omogenea sottraendo 3 da entrambi i membri

$$ 3 - 3 \cos^2 x + 4 \cos x - 3 = 3 - 3 $$

$$ 3 - 3 \cos^2 x + 4 \cos x - 3 = 0 $$

$$ - 3 \cos^2 x + 4 \cos x = 0 $$

Applico la proprietà invariantiva delle equazioni e moltiplico entrambi i membri per (-1).

In questo modo inverto il segno dei termini e rendo più agevole il calcolo.

$$ - 3 \cos^2 x + 4 \cos x = 0 $$

$$ -1 \cdot ( - 3 \cos^2 x + 4 \cos x ) = -1 \cdot 0 $$

$$ 3 \cos^2 x - 4 \cos x = 0 $$

Considero il coseno come un'incognita e lo indico con la variabile di comodo t=cos x

$$ 3 t^2 - 4 t = 0 $$

Ottengo un'equazione di 2° grado che risolvo usando la formula

$$ t = \frac{-b \pm \sqrt{b^2-4ac}}{2a} $$

Dove a=3, b=-4 e c=0

$$ t = \frac{-(-4) \pm \sqrt{(-4)^2-4 \cdot 3 \cdot 0}}{2 \cdot 3} $$

$$ t = \frac{4 \pm \sqrt{16}}{6} $$

$$ t = \frac{4 \pm 4}{6} $$

Quindi, l'equazione 3t²-4t=0 ha due soluzioni

$$ t = \begin{cases} t = \frac{4 + 4}{6} = \frac{8}{6} = \frac{4}{3} \\ \\ t = \frac{4 - 4}{6} = \frac{0}{4} = 0 \end{cases} $$

Nota. Essendo c=0 le stesse soluzioni si possono trovare mettendo in evidenza t. $$ 3 t^2 - 4 t = 0 $$ $$ t (3 t - 4) = 0 $$ L'equazione si annulla se t=0 oppure se t=4/3.

Sapendo che t è il coseno di x

$$ t = \cos x $$

Le soluzioni dell'equazione goniometrica sono

$$ \cos x = \begin{cases} = \frac{4}{3} \\ \\ = 0 \end{cases} $$

Tuttavia, la prima soluzione cos x = 4/3 è impossibile, perché il codominio del coseno è compreso nell'intervallo [-1,1]. Quindi la scarto.

$$ \cos x = \frac{4}{3} = \nexists $$

La seconda soluzione cos x =0 è invece ammissibile perché è compresa nel codominio del coseno [-1,1].

$$ \cos x = 0 $$

Per mettere in evidenza l'incognita x applico l'arcocoseno a entrambi i membri, ossia la funzione inversa del coseno

$$ \arccos ( \cos x ) = \arccos ( 0 ) $$

L'arcocoseno del coseno è l'argomento del coseno ossia l'incognita x.

$$ x = \arccos ( 0 ) $$

L'arcocoseno di zero è π/2 radianti ossia 90°.

Pertanto, la soluzione dell'equazione goniometrica è

$$ x = \arccos ( 0 ) = \frac{\pi}{2} $$

Essendo il seno una funzione periodica con periodo π radianti, non c'è una sola soluzione bensì infinite soluzioni.

$$ x = \frac{\pi}{2} + k \pi $$

Dove k è un numero intero qualsiasi.

Variando k=0,1,-1,2,-2, ... trovo le infinite periodiche soluzioni dell'equazione goniometrica.

Pertanto, la soluzione dell'equazione goniometrica iniziale è x=π/2 a meno di k angoli piatti (π)

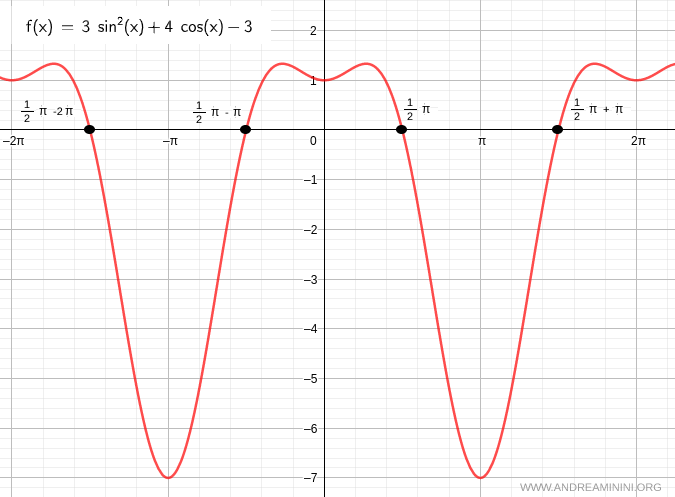
E così via.