Come risolvere l'equazione lineare in seno e coseno con il metodo geometrico
To solve a linear equation in sine and cosine, you can use the geometric/graphical method: $$ a \sin x + b \cos x + c = 0 $$
Create a system that includes the linear trigonometric equation and the fundamental trigonometric identity.
$$ \begin{cases} a \sin x + b \cos x + c = 0 \\ \\ \cos^2 x + \sin^2 x = 1 \end{cases} $$
Then substitute sine and cosine with temporary variables \( s = \sin x \) and \( t = \cos x \):
$$ \begin{cases} a \cdot s + b \cdot t + c = 0 \\ \\ s^2 + t^2 = 1 \end{cases} $$
Finally, solve the system to find the solutions for the variables \( s \) and \( t \).
The values of \( s \) and \( t \) represent a line in the plane, which may intersect the unit circle.
Once the sine and cosine values are found, substitute them back into the system to determine the solutions of the trigonometric equation:
$$ \begin{cases} \cos x = s \\ \\ \sin x = t \end{cases} $$
A Practical Example
Let’s solve the linear equation:
$$ \sqrt{3} \sin x + \cos x = \sqrt{3} $$
Create a system with the fundamental trigonometric identity:
$$ \begin{cases} \sqrt{3} \sin x + \cos x = \sqrt{3} \\ \\ \cos^2 x + \sin^2 x = 1 \end{cases} $$
Substitute sine and cosine with \( s \) and \( t \):
$$ \begin{cases} \sqrt{3} s + t = \sqrt{3} \\ \\ t^2 + s^2 = 1 \end{cases} $$
Solve the system using substitution:
$$ \begin{cases} t = \sqrt{3} - \sqrt{3} s \\ \\ t^2 + s^2 = 1 \end{cases} $$
$$ \begin{cases} t = \sqrt{3} - \sqrt{3} s \\ \\ (\sqrt{3} - \sqrt{3} s)^2 + s^2 = 1 \end{cases} $$
$$ \begin{cases} t = \sqrt{3} - \sqrt{3} s \\ \\ \sqrt{3}^2 - 2 \sqrt{3} \sqrt{3} s+(\sqrt{3} s)^2 + s^2 = 1 \end{cases} $$
$$ \begin{cases} t = \sqrt{3} - \sqrt{3} s \\ \\ 3 - 2 \cdot 3 s+3s^2 + s^2 = 1 \end{cases} $$
$$ \begin{cases} t = \sqrt{3} - \sqrt{3} s \\ \\ 3 - 2 \cdot 3 s+4s^2 = 1 \end{cases} $$
$$ \begin{cases} t = \sqrt{3} - \sqrt{3} s \\ \\ 4s^2 - 6 s +3 - 1 = 0 \end{cases} $$
$$ \begin{cases} t = \sqrt{3} - \sqrt{3} s \\ \\ 4s^2 - 6 s + 2 = 0 \end{cases} $$
The first equation in the system is a quadratic equation: \( 4s^2 - 6s + 2 \) with \( \Delta = b^2 - 4ac = 36 - 4(4 \cdot 2) = 4 \).
$$ s = \frac{-b \pm \sqrt{b^2-4ac}}{2a} $$
$$ s = \frac{-(-6) \pm \sqrt{(-6)^2-4 \cdot 4 \cdot 2}}{2(4)} $$
$$ s = \frac{6 \pm \sqrt{36 - 32}}{8} $$
$$ s = \frac{6 \pm \sqrt{4}}{8} $$
$$ s = \frac{6 \pm 2}{8} $$
$$ s = \frac{6 \pm 2}{8} = \begin{cases} \frac{6 + 2}{8} = \frac{8}{8} = 1 \\ \\ \frac{6 - 2}{8} = \frac{4}{8} = \frac{1}{2} \end{cases} $$
The solutions correspond to the cosine values \( t = \cos x \), which satisfy the trigonometric equation.
Both solutions are compatible with the cosine’s range \([-1, 1]\).
Solution 1
If \( s = 1 \), then \( t = 0 \):
$$ \begin{cases} t = \sqrt{3} - \sqrt{3} s \\ \\ s = 1 \end{cases} $$
$$ \begin{cases} t = \sqrt{3} - \sqrt{3} \cdot 1 \\ \\ s = 1 \end{cases} $$
$$ \begin{cases} t = 0 \\ \\ s = 1 \end{cases} $$
Since \( t = \cos x \) and \( s = \sin x \):
$$ \begin{cases} \cos x = 0 \\ \\ \sin x = 1 \end{cases} $$
The solution to this system is:
$$ x = \frac{\pi}{2} + 2 k \pi $$
Graphically, this solution is point C with Cartesian coordinates \( (0,1) \), forming a 90° angle (\( \pi/2 \)).
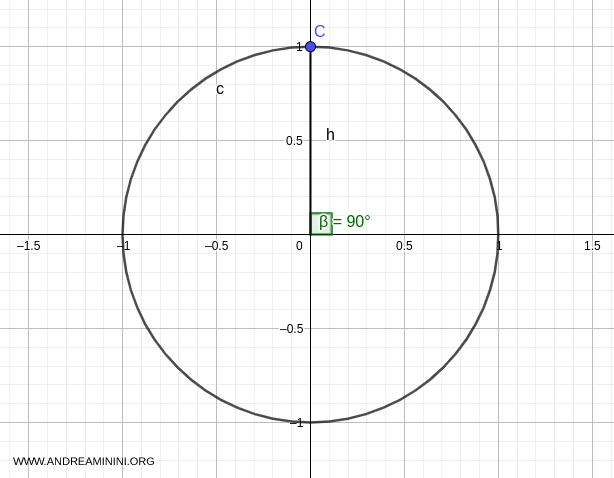
Substituting \( \alpha = \pi/2 \) into the general solution formula gives:
$$ x = \frac{\pi}{2} + 2 k \pi $$
By varying \( k \), all solutions can be found:
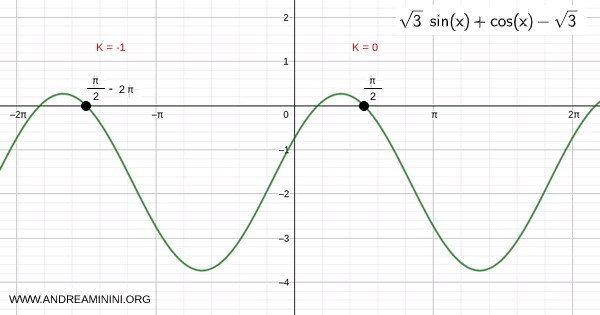
Solution 2
If \( s = \frac{1}{2} \), then \( t = \frac{\sqrt{3}}{2} \):
$$ \begin{cases} t = \sqrt{3} - \sqrt{3} s \\ \\ s = \frac{1}{2} \end{cases} $$
$$ \begin{cases} t = \sqrt{3} - \sqrt{3} \cdot \frac{1}{2} \\ \\ s = \frac{1}{2} \end{cases} $$
$$ \begin{cases} t = \frac{\sqrt{3}}{2} \\ \\ s = \frac{1}{2} \end{cases} $$
Since \( t = \cos x \) and \( s = \sin x \):
$$ \begin{cases} \cos x = \frac{\sqrt{3}}{2} \\ \\ \sin x = \frac{1}{2} \end{cases} $$
The solution to this system is:
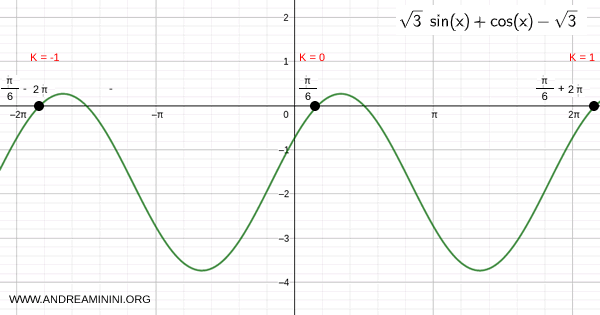
$$ x = \frac{\pi}{6} + 2 k \pi $$
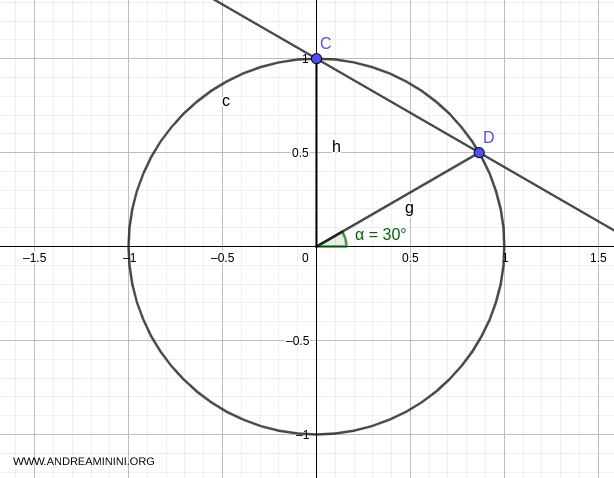
Graphically, this solution is point D with Cartesian coordinates \( \left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right) \) on the unit circle, forming a 30° angle (\( \pi/6 \)).
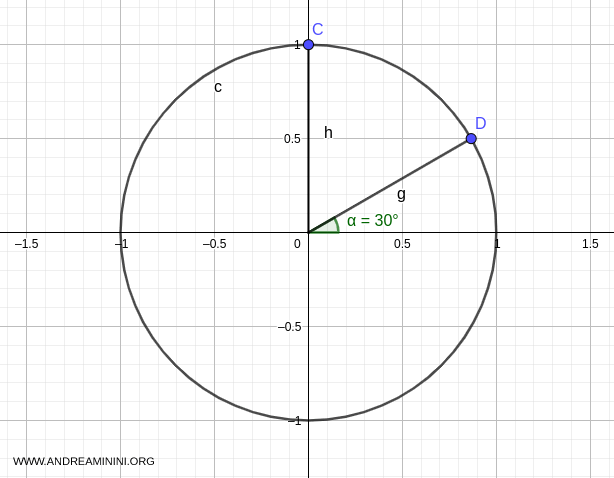
Substituting \( \alpha = \pi/6 \) into the general solution formula gives:
$$ x = \frac{\pi}{6} + 2 k \pi $$
By varying \( k \), all solutions can be found:
Conclusion
The solutions to the linear equation are:
$$ x = \frac{\pi}{2} + 2 k \pi \ \text{or} \ x = \frac{\pi}{6} + 2 k \pi $$
Here, \( k \) is any integer.
These two solutions correspond to points C and D, where the line intersects the unit circle at most twice.