Equazioni goniometriche parametriche
Un'equazione goniometrica parametrica è un'equazione goniometrica elementare o non elementare con un parametro reale (k). Ad esempio $$ \cos x = 2k-1 $$
Le soluzioni di un'equazione goniometrica parametrica dipendono dal valore assegnato al parametro k.
Pertanto, un'equazione goniometrica parametrica potrebbe avere una soluzione per determinati valori di k, più soluzioni o nessuna soluzione per altri valori di k.
Come si studia un'equazione parametrica goniometrica
Per studiare un'equazione goniometrica parametrica analizzo le sue soluzioni al variare del parametro k.
Un esempio pratico
Devo studiare l'equazione goniometrica
$$ \begin{cases} 4 \cos 2x - k +2 = 0 \\ \\ 0 \le x \le \frac{2}{3} \pi \end{cases} $$
Si tratta di un'equazione goniometrica elementare.
E' parametrica in quanto include un parametro k che può assumere qualsiasi valore nell'insieme dei numeri reali.
Inoltre, lo studio dell'equazione è limitato nell'intervallo x ∈ [0, 2π/3].
Metto in evidenza la funzione goniometrica coseno nell'equazione elementare.
$$ \begin{cases} \cos 2x = \frac{k - 2}{4} \\ \\ 0 \le x \le \frac{2}{3} \pi \end{cases} $$
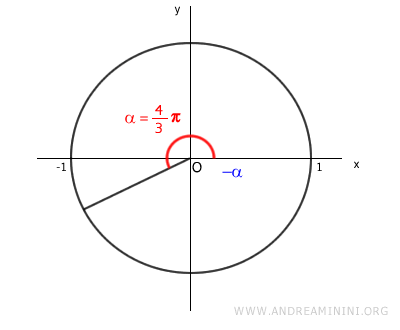
Nell'intervallo x ∈ [0, 2π/3] l'argomento (angolo) della funzione cos 2x varia da 0 a 4π/3 radianti.
$$ 2x = \begin{cases} x = 0 \rightarrow \alpha = 2 \cdot 0 = 0 \\ \\ x = \frac{2}{3} \pi \rightarrow \alpha = 2 \cdot \frac{2}{3} \pi = \frac{4}{3} \pi = \pi + \frac{1}{3} \pi \end{cases}$$
Quindi, la funzione cos 2x assume valori compresi tra -1 e 1 nell'intervallo x ∈ [0, 4π/3].
A questo punto studio quando il lato destro (k-2)/4 dell'equazione parametrica assume valori compresi nell'intervallo [-1,1]
$$ y = \frac{k - 2}{4} $$
Quest'equazione ha i seguenti comportamenti
- Per k=2 è uguale a 0.
- Per k=6 è uguale a 1.
- Per k=-2 è uguale a -1.
- Per k<-2 o k>6 l'equazione assume valori al di fuori dell'intervallo [-1,1].
Quindi, l'equazione parametrica ha almeno una soluzione nell'intervallo k ∈ [-2,6] e nessuna soluzione al di fuori di questo intervallo.
Devo ora capire se nell'intervallo k ∈ [-2,6] l'equazione ha una o più soluzioni.
Nell'intervallo x ∈ [0, 4π/3] la funzione cos 2x assume due volte gli stessi valori quando l'argomento (angolo) è compreso tra π-π/3 e π+π/3
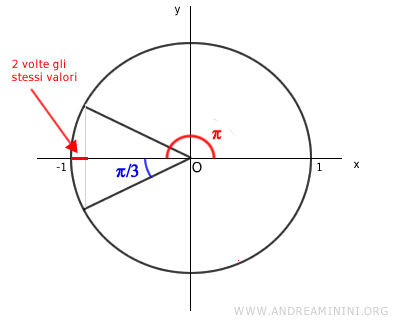
Devo calcolare il valore del coseno quando cos 4π/3
Riscrivo l'argomento del coseno (4/3π) in questa forma algebrica equivalente
$$ \cos \frac{4}{3} \pi = \cos (\pi + \frac{1}{3} \pi) $$
Sapendo che per gli angoli associati del coseno
$$ \cos (\pi + \frac{1}{3} \pi) = \cos (\pi - \frac{1}{3} \pi) $$
e che
$$ \cos (\pi - \frac{1}{3} \pi) = - \cos ( \frac{1}{3} \pi) $$
Ho ricondotto il calcolo del coseno di 4/3 π nel primo quadrante. In questo modo è più facile da calcolare.
$$ \cos \frac{4}{3} \pi = - \cos ( \frac{1}{3} \pi) $$
Sapendo che il coseno di π/3 (ossia 60°) è 1/2
$$ \cos \frac{4}{3} \pi = - \frac{1}{2} $$
Pertanto, l'equazione goniometrica ha due soluzioni quando cos 2x ∈ [-1,-1/2] mentre ha un'unica soluzione quando cos 2x ∈ (-1/2, 1] .
$$ \begin{cases} \cos 2x = \frac{k - 2}{4} \\ \\ 0 \le x \le \frac{2}{3} \pi \end{cases} $$
A questo punto studio quando il lato destro dell'equazione parametrica assume valori compresi nell'intervallo [-1,-1/2]
$$ y = \frac{k - 2}{4} $$
L'equazione assume il valore y=-1 quando k = -2
$$ -1 = \frac{k - 2}{4} $$
$$ -1(4)+2 = k $$
$$ k = -2 $$
L'equazione assume il valore y=-1/2 quando k = 0
$$ - \frac{1}{2} = \frac{k - 2}{4} $$
$$ - 4 \frac{1}{2} + 2 = k $$
$$ - 2 + 2 = k $$
$$ k = 0 $$
Pertanto, nell'intervallo k ∈ [-2, 0] l'equazione goniometrica ha due soluzioni.
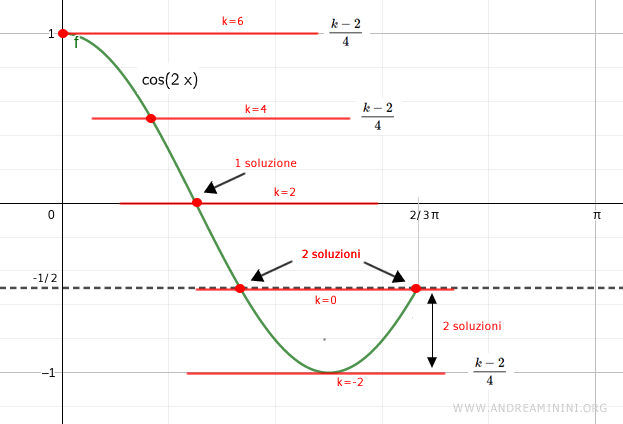
Viceversa, nell'intervallo k ∈ (0, 6] l'equazione goniometrica ha una sola soluzione.
Per tutti gli altri valori k ∉ [-2, 6] l'equazione goniometrica non ha soluzioni.
E così via.
