Sistema di disequazioni goniometriche
Un sistema di disequazioni goniometriche è composto da due o più disequazioni goniometriche con la stessa incognita nell'argomento. Ad esempio $$ \begin{cases} 2 \sin x \le 1 \\ \\ 2 \cos x < \sqrt{3} \end{cases} $$
Come risolvere un sistema di disequazioni goniometriche
Per risolvere un sistema di disequazioni
- Trovo la soluzione di ogni singola disequazione goniometrica
- Verifico se esiste un'intersezione tra le soluzioni delle disequazioni
La soluzione del sistema di disequazioni sono i valori dell'incognita x che soddisfano contemporaneamente tutte le disequazioni del sistema.
Un esempio pratico
Devo risolvere il sistema di disequazioni goniometriche
$$ \begin{cases} 2 \sin x \le 1 \\ \\ 2 \cos x < \sqrt{3} \end{cases} $$
Trovo le soluzioni della prima disequazione
$$ 2 \sin x \le 1 $$
$$ \sin x \le \frac{1}{2} $$
L'equazione elementare sin x = 1/2 associata alla disequazione è soddisfatta quando la x assume i seguenti valori
$$ x = \frac{\pi}{6} + 2k \pi \ ∨ \ x = \pi-\frac{\pi}{6} + 2k $$
$$ x = \frac{\pi}{6} + 2k \pi \ ∨ \ x = \frac{6\pi - \pi}{6} + 2k $$
$$ x = \frac{\pi}{6} + 2k \pi \ ∨ \ x = \frac{5}{6} \pi + 2k $$
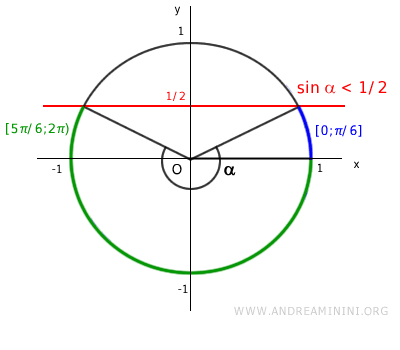
Pertanto, nell'intervallo (0,2π) la disequazione è soddisfatta negli intervalli [0,π/6] e [5π/6, 2π)
Trovo le soluzioni della seconda disequazione
$$ 2 \cos x < \sqrt{3} $$
$$ \cos x < \frac{ \sqrt{3} }{2} $$
L'equazione elementare cos x = √3/2 associata alla disequazione è soddisfatta nei valori x
$$ x = \frac{\pi}{6} + 2k \pi \ ∨ \ x = -\frac{\pi}{6} + 2k $$
Dove -π/6 lo riscrivo nell'intervallo di riferimento (0,2π) come 2π-π/6
$$ x = \frac{\pi}{6} + 2k \pi \ ∨ \ x = 2 \pi -\frac{\pi}{6} + 2k $$
$$ x = \frac{\pi}{6} + 2k \pi \ ∨ \ x = \frac{12 \pi - \pi}{6} + 2k $$
$$ x = \frac{\pi}{6} + 2k \pi \ ∨ \ x = \frac{11 \pi }{6} + 2k $$
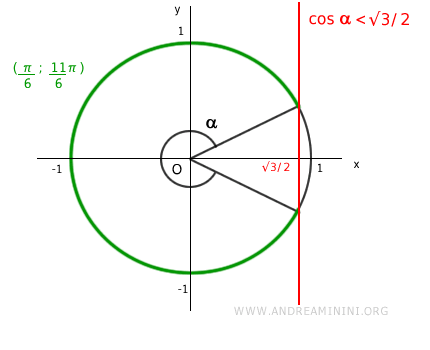
Quindi, nell'intervallo (0,2π) la disequazione è soddisfatta nell'intervallo (π/6,11π/6)
Ora verifico se esiste un'intersezione tra le soluzioni delle due disequazioni del sistema
$$ \{ \ [ 0 \ ; \ \frac{\pi}{6} ] \ ∪ \ [ \frac{5\pi}{6} \ ; \ 2 \pi ] \ \} ∧ \{ ( \ \frac{\pi}{6} \ ; \ \frac{11 \pi}{6} ) \ \} $$
$$ [ \ \frac{5\pi}{6} \ ; \ \frac{11 \pi}{6} ) $$
L'intersezione esiste, quindi il sistema ha delle soluzioni.
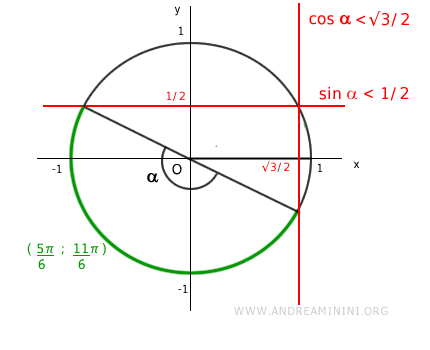
Nel periodo (0,2π) le soluzioni del sistema di disequazioni goniometriche sono i valori dell'incognita x compresi nell'intervallo [5π/6 ; 11π/6)
Considerando anche tutte le altre infinite soluzioni periodiche, il sistema è soddisfatto negli intervalli
$$ [ \ \frac{5\pi}{6} + 2k \pi \ ; \ \frac{11 \pi}{6} + 2k \pi ) $$
Dove k è un numero intero qualsiasi.
Verifica su Geogebra
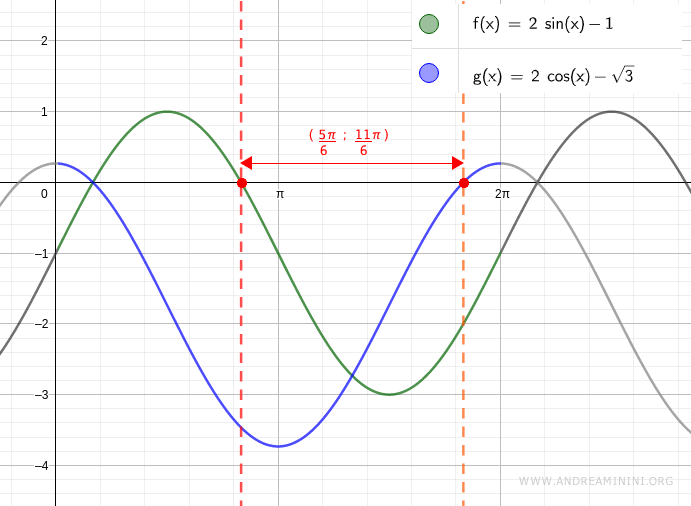
Per ulteriore conferma analizzo il grafico delle due funzioni goniometriche nel periodo (0,2π).
Le funzioni sono entrambe negative nell'intervallo (5π/6 ; 11π/6).
E così via.
