Le operazioni tra polinomi
Le principali operazioni matematiche tra due polinomi
L'addizione tra polinomi
La somma di due polinomi è un polinomio con tutti i termini dei due polinomi ridotto in forma normale.
Esempio. Considero i polinomi $$ P(x): \ 2x^2 + 3x + 2 $$ $$ Q(x): \ 4x^2 + 5x + 6 $$ La somma dei due polinomi è un polinomio con i termini di entrambi i polinomi $$ P(x)+Q(x) = (2x^2 + 3x + 2)+ (4x^2 + 5x + 6) $$ che successivamente riduco in forma normale $$ P(x)+Q(x) = 2x^2 + 3x + 2+ 4x^2 + 5x + 6 $$ $$ P(x)+Q(x) = x^2 \cdot (2+4) + x(3+5) + 2+6 $$ $$ P(x)+Q(x) = 6x^2 + 8x + 8 $$
La sottrazione tra polinomi
La differenza tra due polinomi si ottiene sommando al primo polinomio (minuendo) il secondo polinomio (sottraendo) cambiato di segno (polinomio opposto).
Esempio. Considero i polinomi $$ P(x): \ 2x^2 + 3x + 2 $$ $$ Q(x): \ 4x^2 + 5x + 6 $$ Per calcolare la differenza P(x)-Q(x) calcolo la somma algebrica del primo polinomio P(x) con il secondo polinomio Q(x) cambiato di segno $$ P(x)-Q(x) = (2x^2 + 3x + 2)+ (-4x^2 - 5x - 6) $$ che successivamente riduco in forma normale $$ P(x)-Q(x) = 2x^2 + 3x + 2- 4x^2 - 5x - 6 $$ $$ P(x)-Q(x) = x^2 \cdot (2-4) + x(3-5) + 2-6 $$ $$ P(x)-Q(x) = -2x^2 -2x - 4 $$
La moltiplicazione tra polinomi
Per moltiplicare due polinomi si applica la proprietà distributiva della moltiplicazione rispetto all'addizione, il risultato è un polinomio che ha per termini la somma dei prodotti di ogni termine del primo polinomio per ogni termine del secondo polinomio.
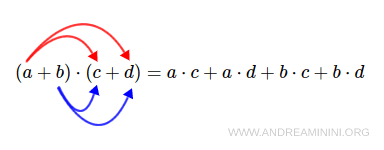
Il grado del polinomio prodotto è uguale alla somma dei gradi dei polinomi fattori.
Esempio. Considero il prodotto tra due polinomi fattori $$ ( 2a + 3b) \cdot (3a - 4b) $$ Applico la proprietà associativa e la proprietà distributiva della moltiplicazione rispetto all'addizione $$ 2a \cdot (3a - 4b) + 3b \cdot (3a - 4b) $$ $$ 6a^2 - 8ab + 9ab - 12b^2 $$ Infine, riduco il polinomio prodotto alla forma normale $$ 6a^2 + ab - 12b^2 $$ Il polinomio prodotto è di grado due, pari alla somma dei gradi dei due polinomi fattori.
In alcuni casi particolari posso giungere al risultato senza svolgere i calcoli applicando i prodotti notevoli.
Ecco qualche esempio pratico di prodotto notevole della moltiplicazione tra polinomi.
- Il prodotto tra la somma e la differenza di due monomi $$ (a+b) \cdot (a-b) = a^2 - b^2 $$
- Il quadrato di un binomio $$ (a+b) \cdot (a+b) = (a+b)^2 = a^2 +2ab+ b^2 $$
- Il quadrato di un trinomio $$ (a+b+c) \cdot (a+b+c) = (a+b+c)^2 = a^2+b^2+c^2 +2ab+2ac+2bc $$
- Il quadrato di un quadrinomio $$ (a + b + c + d)^2 = a^2 + b^2 + c^2 + d^2 + \\ + 2ab + 2ac + 2ad + 2bc + 2bd + 2cd $$
- Il cubo di un binomio $$ (a+b)^2 \cdot (a+b) = (a+b)^3 = a^3 +3a^2b+3ab^2+ b^3 $$
La divisione tra polinomi
Un polinomio A (dividendo) è divisibile per un monomio/polinomio B (divisore) non nullo se e solo se esiste un polinomio quoziente Q tale che il prodotto dei polinomi B·Q + R è uguale al polinomio A $$ A:B = Q \ \ \Leftrightarrow \ \ \ B \cdot Q = A$$ Dove Re è un eventuale polinomio resto.
La divisione è possibile solo se il polinomio dividendo è di grado maggiore o uguale al polinomio divisore.
Il grado del polinomio quoziente è uguale alla differenza tra il grado del polinomio dividendo e quello del polinomio divisore.
Esempio. Considero la divisione tra i polinomi P(x) e Q(x) $$ P(x): \ x^2+5x+7 $$ $$ Q(x): \ x+3 $$ In questo caso il polinomio quoziente esiste ed è il polinomio Q(x) $$ Q(x): \ x+2 $$ Per trovare il polinomio quoziente Q(x) esiste una procedura abbastanza semplice che ho già spiegato in un altro mio appunto ( come dividere due polinomi ) a cui rimando per ogni approfondimento.
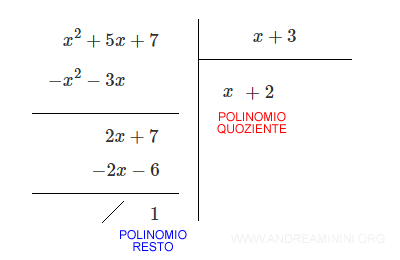
Il polinomio quoziente Q(x) è di grado 1. E' uguale alla differenza tra il grado del polinomio dividendo (2) e quello del polinomio divisore (1).
E così via.
