Il cubo di un binomio

Il cubo di un binomio (a+b)³ è un quadrinomio composto dalla somma algebrica dei cubi dei due termini, il triplo del quadrato del primo termine per il secondo, il triplo del quadrato del secondo termine per il primo. $$(a+b)^3 = a^3+3a^2b+3ab^2+b^3$$

Un esempio pratico

Esempio 1

Considero un binomio elevato alla terza

$$(2a+4b)^3$$

Espando il cubo del binomio usando la formula iniziale

$$(2a+4b)^3 = (2a)^3 + 3 \cdot (2a)^2 \cdot (4b) + 3 \cdot (2a) \cdot (4b)^2 + (4b)^3$$

$$(2a+4b)^3 = 8a^3 + 3 \cdot 4a^2 \cdot 4b + 3 \cdot 2a \cdot 16b^2 + 64b^3$$

$$(2a+4b)^3 = 8a^3 + (3 \cdot 4 \cdot 4) \cdot a^2b + (3 \cdot 2 \cdot 16) \cdot ab^2 + 64b^3$$

$$(2a+4b)^3 = 8a^3 + 48a^2b + 96ab^2 + 64b^3$$

Esempio 2

Considero il cubo del binomio con il secondo termine negativo

$$(2a-3b)^3$$

$$(2a-3b)^3 = (2a)^3 + 3 \cdot (2a)^2 \cdot (-3b) + 3 \cdot (2a) \cdot (-3b)^2 + (-3b)^3$$

$$(2a-3b)^3 = 8a^3 + 3 \cdot 4a^2 \cdot (-3b) + 3 \cdot 2a \cdot 9b^2 -27b^3$$

$$(2a-3b)^3 = 8a^3 + [3 \cdot 4 \cdot (-3)] \cdot a^2b + (3 \cdot 2 \cdot 9) \cdot ab^2 -27b^3$$

$$(2a-3b)^3 = 8a^3 - 36a^2b + 54ab^2 -27b^3$$

La dimostrazione

Il cubo del binomio è il binomio moltiplicato per se stesso tre volte

$$(a+b)^3 = (a+b) \cdot (a+b) \cdot (a+b)$$

Il che equivale a moltiplicare il binomio per il quadrato del binomio.

$$(a+b)^3 = (a+b)^2 \cdot (a+b)$$

Il calcolo del quadrato del binomio è già dimostrato (vedi dimostrazione).

Quindi, applico la regola ed espando il quadrato del binomio

$$(a+b)^3 = (a^2+2ab+b^2) \cdot (a+b)$$

Poi calcolo il prodotto algebrico tra i due termini dell'espressione

$$(a+b)^3 = (a^2+2ab+b^2) \cdot a + (a^2+2ab+b^2) \cdot b$$

$$(a+b)^3 = a^3+2a^2b+ab^2 + a^2b+2ab^2+b^3$$

$$(a+b)^3 = a^3+(2a^2b+ a^2b)+(ab^2 +2ab^2)+b^3$$

In questo modo ottengo la formula del cubo del trinomio che volevo dimostrare.

$$(a+b)^3 = a^3+3a^2b+3ab^2+b^3$$

La dimostrazione geometrica

Considero un cubo di lato A+B

Il volume del cubo è il lato alla terza, quindi $(A+B)^3$

Ora scompongo in 8 parti più piccole (2 cubi e 6 parallelepipedi) e calcolo il volume per ciascuna parte.

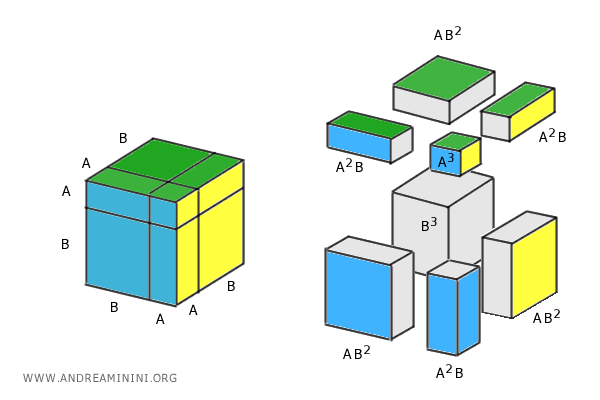
Il volume totale del cubo iniziale è dato dalla somma dei volumi dei pezzi più piccoli.

$$(A+B)^3 = A^3 + B^3 + AB^2 + AB^2 + AB^2 + A^2B   + A^2B + A^2B$$

$$(A+B)^3 = A^3 + B^3 + 3AB^2 + 3A^2B$$

Questo mostra visivamente come si arriva alla formula del cubo del binomio.

E così via.