La divisione tra polinomi

Cos'è la divisione tra due polinomi

Dividere un polinomio A(x) per un polinomio B(x) $$ A(x):B(x) $$ vuol dire trovare un polinomio quoziente Q(x) tale che $$ A(x) = B(x) \cdot Q(x) + R $$ dove A(X) è il polinomio "dividendo", B(x) è il polinomio "divisore", R è il polinomio resto.

Se il resto della divisione è nullo (R=0), allora il polinomio A(x) è divisibile per il polinomio B(x).

$$ A(x):B(x) = \frac{A(x)}{B(x)} = Q(x) \ \ \ \text{con R=0} $$

In caso contrario, se il resto non è nullo, il polinomio A(x) non è divisibile per il polinomio B(x)

Nota. La divisione tra due polinomi A(x):B(x) è sempre una frazione algebrica ma non è detto che sia anche un polinomio. $$ A(x):B(x) = \frac{A(x)}{B(x)} $$ La divisione tra due polinomi è un polinomio solo nel caso in cui il risultato della divisione è un polinomio quoziente Q(x) con resto nullo R=0. Ad esempio, la divisione tra i polinomi x+1 e x-1 non è un polinomio $$ \frac{x+1}{x-1} $$ perché il resto della divisione non è nullo (R=2). Pertanto il rapporto (x+1)/(x-1) non è polinomio ma è comunque una frazione algebrica.

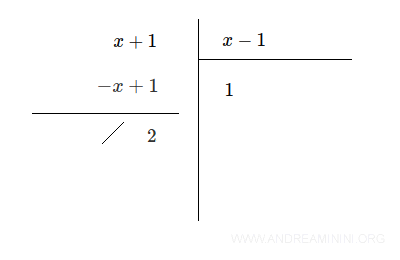
Come dividere due polinomi

Per trovare il polinomio quoziente Q(x) seguo questo algoritmo

Scrivo il polinomio dividendo P(x) e il polinomio divisore Q(x) come se fosse una normale divisione.

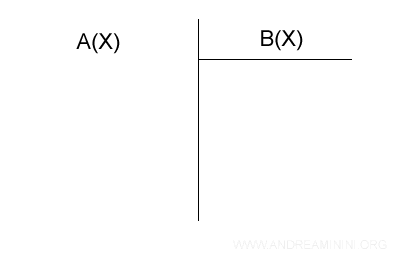
Nota. Se il polinomio divisore è di grado più alto rispetto al polinomio dividendo, il polinomio quoziente è Q(x)=0 e l'algoritmo termina qui.

Ad esempio, se la divisione è tra P(x)=x²+5x+7 e Q(x)=x+3

Ora divido il monomio di grado più alto del dividendo P(x) per il monomio di grado più alto del divisore Q(x) e scrivo il quoziente nel risultato.

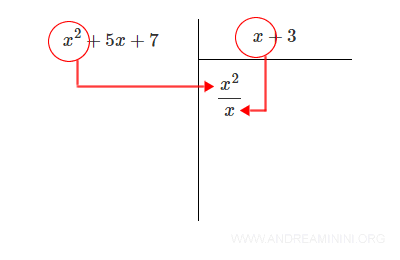
In questo caso il monomio di grado più alto del polinomio dividendo è x² mentre quello del polinomio divisore è x.

Il monomio quoziente è x²/x = x

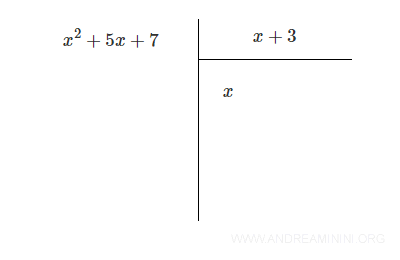
Ora moltiplico il monomio quoziente x per il polinomio divisore (x+3).

$$ x \cdot (x+3) = x^2 + 3x $$

Poi scrivo il polinomio prodotto x²+3x con segno opposto -(x²+3x) = -x² -3x sotto al polinomio dividendo.

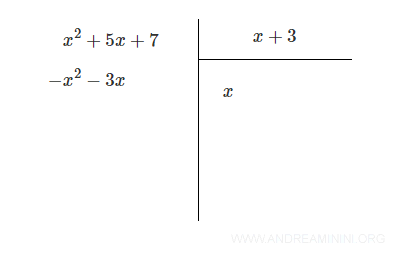
Infine traccio una linea e sommo il polinomio divisore x²+5x+7 con il polinomio -x²-3x

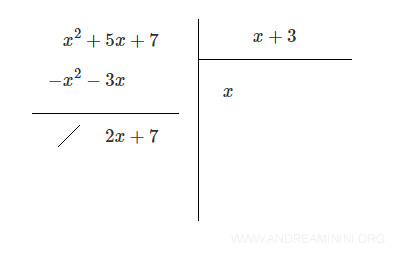
A questo punto ricomincio tutto daccapo.

Divido il monomio di grado più alto del polinomio 2x+7 con il monomio di grado più alto del polinomio divisore x+3.

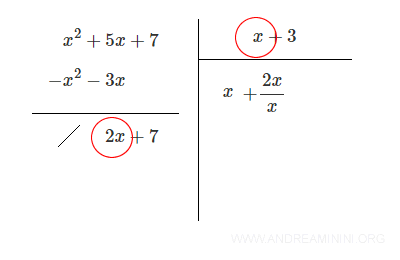
In questo caso il monomio di grado più alto del polinomio 2x+7 è 2x mentre quello del polinomio divisore x+3 è x.

Il monomio quoziente è 2x/x = 2

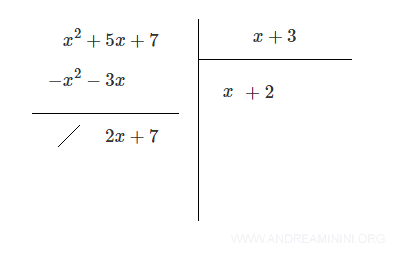
Ora moltiplico il monomio quoziente 2 per il polinomio divisore (x+3).

$$ 2 \cdot (x+3) = 2x + 6 $$

Poi scrivo il polinomio prodotto 2x+6 con segno opposto -(2x+6) = -2x -6 sotto al polinomio 2x+7

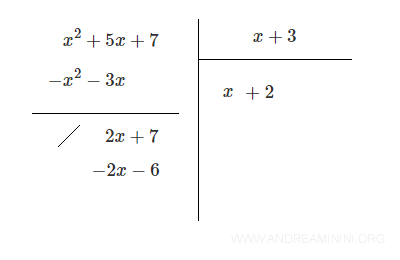
Infine traccio una linea e sommo il polinomio -2x-6 con il polinomio x+2

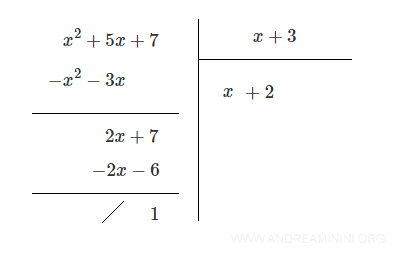
ll processo termina qui perché il polinomio resto (1) è di grado inferiore al polinomio divisore (x+3). Quindi, un'ulteriore divisione è impossibile.

Pertanto, il risultato della divisione è il polinomio quoziente Q(x)=x+2 con resto R=1

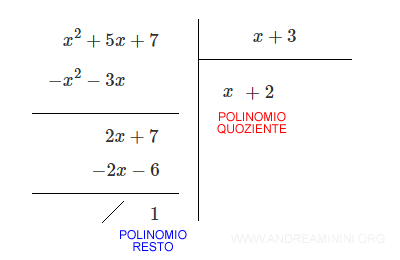
In questo caso il risultato non è un polinomio perché il resto non è nullo (R=1).

Verifica. Verifico se il risultato è corretto. $$ Q(x) = x+2 $$ $$ R(x) = 1 $$ Il polinomio dividendo è uguale al prodotto tra il polinomio divisore e il polinomio quoziente più il resto $$ A(x) = B(x) \cdot Q(x) + R(x) $$ Sapendo che B(x)=x+3 , Q(x)= x+2 e R(x)=1 $$ A(x) = (x+3) \cdot (x+2) + 1 $$ Svolgo i calcoli. $$ A(x) = x^2 + 2x +3x +6 + 1 $$ $$ A(x) = x^2 + 5x +7 $$ Il risultato è il polinomio dividendo A(x)=x²+5x+7. Il risultato è corretto.

Esempio 2

Considero la divisione tra due polinomi A(x):-3x⁴+14x³-13x²+2 e B(x): 3x²-2x-1

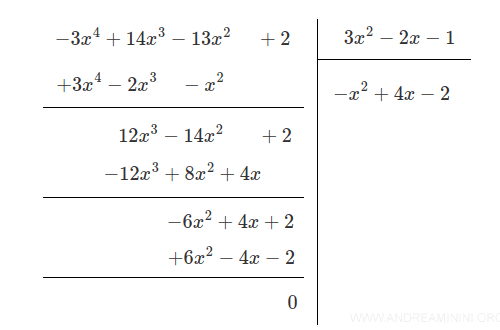
In questo caso il polinomio quoziente è -x²+4x-2 con resto R=0

Quindi, il risultato della divisione è a sua volta un polinomio.

Verifica. Verifico se il risultato è corretto. $$ Q(x) = -x^2+4x-2 $$ $$ R(x) = 0 $$ Il polinomio dividendo è uguale al prodotto tra il polinomio divisore e il polinomio quoziente più il resto $$ A(x) = B(x) \cdot Q(x) + R(x) $$ Sapendo che B(x)=3x²-2x-1 , Q(x)= -x²+4x-2 e R(x)=0 $$ A(x) = (3x^2-2x-1) \cdot (-x^2+4x-2) + 0 $$ Svolgo i calcoli. $$ A(x) = -3x^4+2x^3+x^2+12x^3-8x^2-4x-6x^2+4x+2 $$ $$ A(x) = -3x^4 + 14x^3 - 13x^2 +2 $$ Il risultato è il polinomio dividendo A(x)=-3x⁴+14x³-13x²+2. Il risultato è corretto.

La regola di Ruffini

La regola di Ruffini è un procedimento alternativo per calcolare la divisione tra i polinomi quando il polinomio al divisore è un binomio del tipo x-k $$ \frac{P(x)}{(x-k)} $$

Si applica solo se il divisore è un binomio (x-k) dove k è un numero reale qualsiasi.

Quindi, a differenza del metodo precedente, la regola di Ruffini non è un metodo generale per calcolare la divisione polinomiale.

Esempio

Devo calcolare la divisione è tra P(x)=x²+5x+7 e Q(x)=x+3

$$ \frac{x^2+5x+7}{x+3} $$

Il divisore è un binomio del tipo (x-k) con k=-3, quindi posso usare la regola di Ruffini.

Scrivo sulla prima riga i coefficienti del polinomio dividendo con il termine noto (7) dopo la seconda linea verticale.

$$ \begin{array}{c|lc|r} & 1 & 5 & 7 \\ & & & \\ \hline & & & \end{array} $$

Scrivo sulla seconda riga il valore opposto del termine noto del polinomio divisore prima della prima linea verticale.

In questo caso il termine noto del divisore è 3, quindi il suo valore opposto è -3

$$ \begin{array}{c|lc|r} & 1 & 5 & 7 \\ \color{red}{-3}& & & \\ \hline & & & \end{array} $$

Faccio scendere il primo coefficiente sulla prima riga fino alla terza riga.

$$ \begin{array}{c|lc|r} & 1 & 5 & 7 \\ -3& & & \\ \hline &\color{red}{1} & & \end{array} $$

Poi moltiplico il coefficiente appena sceso (1) sulla terza riga per -3 e scrivo il risultato nella seconda riga della colonna successiva

$$ \begin{array}{c|lc|r} & 1 & 5 & 7 \\ -3& & \color{red}{-3 \cdot 1} & \\ \hline &1 & & \end{array} $$

$$ \begin{array}{c|lc|r} & 1 & 5 & 7 \\ -3& & \color{red}{-3} & \\ \hline &1 & & \end{array} $$

Calcolo la somma algebrica della seconda colonna e scrivo il risultato sulla terza riga.

$$ \begin{array}{c|lc|r} & 1 & 5 & 7 \\ -3& & -3 & \\ \hline &1 & \color{red}{5-3} & \end{array} $$

$$ \begin{array}{c|lc|r} & 1 & 5 & 7 \\ -3& & -3 & \\ \hline &1 & \color{red}{2} & \end{array} $$

Poi moltiplico la somma (2) per -3 e scrivo il risultato nella seconda riga della colonna successiva

$$ \begin{array}{c|lc|r} & 1 & 5 & 7 \\ -3& & -3 & \color{red}{ -3 \cdot2} \\ \hline &1 & 2 & \end{array} $$

$$ \begin{array}{c|lc|r} & 1 & 5 & 7 \\ -3& & -3 & \color{red}{-6} \\ \hline &1 & 2 & \end{array} $$

Calcolo la somma algebrica della terza colonna e scrivo il risultato sulla terza riga.

$$ \begin{array}{c|lc|r} & 1 & 5 & 7 \\ -3& & -3 & -6 \\ \hline &1 & 2 & \color{red}{7-6} \end{array} $$

$$ \begin{array}{c|lc|r} & 1 & 5 & 7 \\ -3& & -3 & -6 \\ \hline &1 & 2 & \color{red}{1} \end{array} $$

I valori tra le barre verticali sono i coefficienti del polinomio quoziente mentre il valore dopo la seconda barra verticale è il resto della divisione.

Considerando che il polinomio dividendo x²+5x+7 è di grado 2 e il polinomio divisore x+3 è di grado 1, il polinomio quoziente deve essere di grado 1

$$ Q(x) = x+2 $$

$$ R=1 $$

Nota. Il polinomio quoziente è sempre di grado inferiore rispetto al polinomio dividendo. Il grado del polinomio quoziente è uguale alla differenza tra il grado del polinomio dividendo e quello del polinomio divisore. In questo caso il grado del polinomio dividendo x²+5x+7 è 2 mentre il grado del polinomio divisore x+3 è 1, quindi il polinomio quoziente è di grado 1 (ossia 2-1)

E così via.