La potenza ennesima di un binomio
Per sviluppare la potenza ennesima di un binomio (a+b)n applico la seguente formula $$ (a+b)^n = c_0a^n + c_1a^{n-1}b + c_2a^{n-2}b^2 + ... + c_{n-1}ab^{n-1} + c_nb^n $$ sostituendo i coefficienti c0,c1,c2...,cn-1,cn con i numeri che si trovano nella riga ennesima (n) del triangolo di Tartaglia.
Come sviluppare la potenza di un binomio
Per risolvere la potenza di un binomio con esponente n
$$ (a+b)^n $$
Scrivo le potenze da n a 0 della prima lettera (a) del binomio, dove n è l'esponente del binomio.
$$ a^n \ a^{n-1} \ ... \ a^1 \ a^0 $$
Poi scrivo le potenze da 0 a n della seconda lettera (b) del binomio
$$ b^0 \ b^1 \ ... \ b^{n-1} \ b^n $$
Moltiplico tra loro le potenze di a e b che occupano la stessa posizione nella successione
$$ a^nb^0 \ a^{n-1}b^1 \ ... \ a^1b^{n-1} \ a^0b^n $$
Trasformo la successione di prodotti in una somma algebrica
$$ a^nb^0 + a^{n-1}b^1 + ... + a^1b^{n-1} + a^0b^n $$
Sapendo che qualsiasi numero elevato a zero è uguale a uno, posso eliminare a0=1 e b0=1 dalla somma
$$ a^n \cdot 1 + a^{n-1}b^1 + ... + a^1b^{n-1} + 1 \cdot b^n $$
$$ a^n + a^{n-1}b^1 + ... + a^1b^{n-1} + b^n $$
Moltiplico ciascun termine della somma per un coefficiente c da 0 a n
$$ c_0a^n + c_1a^{n-1}b^1 + ... + c_{n-1}a^1b^{n-1} + c_nb^n $$
Infine, utilizzo il triangolo di Tartaglia per trovare i coefficienti c0,c1,c2,...,cn.
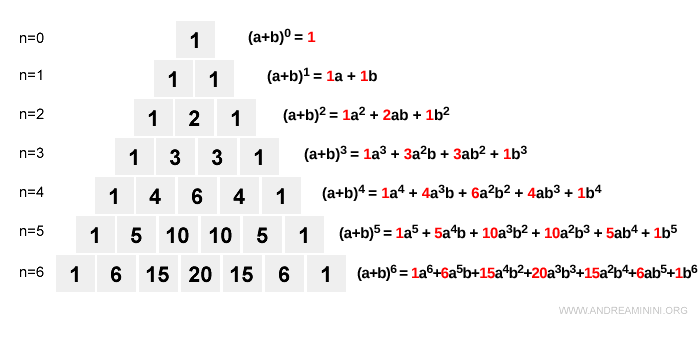
Come si sviluppa il Triangolo di Tartaglia? Per costruire il triangolo di Tartaglia rappresento un triangolo con i vertici uguali a 1 poi scendo di una riga verso il basso mantenendo sempre 1 nei vertici e scrivendo in ciascun spazio vuoto all'interno del triangolo la somma della coppia dei numeri che si trovano nella riga precedente. E via dicendo di riga in riga.
Per vedere il processo passo dopo passo rimando agli appunti sul triangolo di Tartaglia.
Il risultato finale è l'espansione della potenza ennesima del binomio.
Un esempio pratico
Considero un binomio elevato alla quarta (n=4)
$$ (a+b)^4 $$
Scrivo la somma algebrica dei prodotti delle potenze decrescenti (da n a 0) della prima lettera (a) con le potenze crescenti (da 0 a n) della seconda lettera (b) del binomio.
In questo caso, l'esponente della potenza del binomio è n=4
$$ a^4b^0 + a^3b^1 + a^2b^2 + a^1b^3 + a^0b^4 $$
Evito di scrivere le potenze elevate a zero ed elimino l'esponente nelle potenze elevate a uno.
$$ a^4 + a^3b + a^2b^2 + ab^3 + b^4 $$
Aggiungo i coefficienti alla somma algebrica delle potenze
$$ c_0a^4 + c_1a^3b + c_2a^2b^2 + c_3ab^3 + c_4b^4 $$
Individuo i coefficienti c0,...,c4 nel triangolo di Tartaglia.
In questo caso la riga che mi interessa è la riga n=4
Leggo la riga n=4 del triangolo e ottengo i coefficienti che devo utilizzare c0=1, c1=4, c2=6, c3=4, c4=1
$$ c_0a^4 + c_1a^3b + c_2a^2b^2 + c_3ab^3 + c_4b^4 $$
$$ 1 \cdot a^4 + 4 \cdot a^3b + 6 \cdot a^2b^2 + 4 \cdot ab^3 + 1 \cdot b^4 $$
$$ a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4 $$
Il risultato finale è lo sviluppo del binomio (a+b) elevato alla quarta.
$$ (a+b)^4 = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4 $$
Osservazioni
Alcune osservazioni varie
- La regola dello sviluppo del quadrato binomio venne ideata nel XI secolo dal matematico arabo al-Karaji. Riuscì a calcolare le potenze di (a+b)n fino a n=12.
E così via.
