Raccoglimento a fattore comune
Cos'è il raccoglimento a fattore comune
Il raccoglimento a fattore comune è una regola di scomposizione (fattorizzazione) di un polinomio P(x) di grado n in un prodotto di polinomi di grado inferiore $$ P_n(x) = A_s(x) \cdot B_t(x) $$ con s+t=n
La somma dei gradi dei polinomi fattori (s+t) è uguale al grado (n) del polinomio iniziale
Quando una somma di addendi ha uno stesso fattore in comune, posso raccogliere il fattore comune mettendolo in evidenza e moltiplicarlo per la somma degli altri termini.
$$ (xa+xb) = x \cdot (a+b) $$
Nota. Questo risultato lo ottengo applicando la proprietà distributiva della moltiplicazione rispetto all'addizione x·(a+b)=x·a+x·b in senso contrario x·a+x·b =x·(a+b). $$ x \cdot a + x \cdot b = x \cdot (a+b) $$ La proprietà distributiva della moltiplicazione rispetto all'addizione vale sia a destra che a sinistra perché la moltiplicazione soddisfa la proprietà commutativa. $$ x \cdot (a+b) = (a+b) \cdot x $$ Quindi, anche il raccoglimento a fattore comune posso farlo sia a destra che a sinistra. $$ x \cdot a + x \cdot b = x \cdot (a+b) = (a+b) \cdot x $$ Il risultato è sempre lo stesso.
Un esempio pratico
Esempio 1
Considero il polinomio di primo grado
$$ 3a + 3b $$
I due addendi hanno un fattore in comune (3).
Raccolgo il fattore comune (3) e lo moltiplico per la somma degli altri termini.
$$ 3 \cdot (a + b) $$
Questo è il risultato del raccoglimento a fattore comune.
Nota. Posso fare il raccoglimento a fattore comune sia a destra che a sinistra. $$ 3a + 3b = 3 \cdot (a+b) = (a+b) \cdot 3 $$ Il risultato finale non cambia perché la moltiplicazione soddisfa la proprietà commutativa.
Nota 2. Quando il fattore in comune è un coefficiente numerico, come in questo esempio, la fattorizzazione è il prodotto tra un polinomio di grado zero e un polinomio dello stesso grado del polinomio iniziale. In questo caso n=1. Quindi, in questo caso particolare il prodotto non è tra polinomi di grado inferiore (come detto nella definizione) poiché uno dei due polinomi fattori è di grado zero (il numero). Ad ogni modo, la somma dei gradi dei polinomi fattori (0+1) è sempre uguale al grado del polinomio iniziale (n=1). $$ \underbrace{3a + 3b}_{n=1} = \underbrace{3}_{0} \cdot \underbrace{(a+b)}_{1} = \underbrace{(a+b)}_{1} \cdot \underbrace{3}_{0} $$
Esempio 2
Tutti i termini del seguente polinomio contengono il fattore x
$$ 2x^3 - 5x^2 + x $$
Raccolgo il fattore comune (x) e lo metto in evidenza
$$ x \cdot (2x^2-5x+1) $$
In questo modo ottengo il prodotto tra un polinomio di primo grado (x) e un polinomio di secondo grado (2x2-5x+1).
Nota. La somma dei gradi dei polinomi fattori è sempre uguale al grado del polinomio iniziale. In questo caso la somma dei gradi dei polinomi fattori 1+2 è uguale al grado n=3 del polinomio iniziale.
Nella forma ridotta diventa molto più semplice capire quando il polinomio si annulla perché basta applicare la legge dell'annullamento del prodotto.
$$ x \cdot (2x^2-5x+1) $$
Ad esempio, se il primo fattore (il monomio x) è x=0 il prodotto si annulla.
Quindi x=0 è una delle soluzioni dell'equazione 2x3 - 5x2 + x=0.
Nota. Quando una soluzione del problema è x=0 si parla di soluzione banale.
Per trovare le altre soluzioni mi basta risolvere l'equazione di 2° grado 2x2-5x+1=0 al secondo fattore
Sapendo che i coefficienti sono a=2, b=-5 e c=1
$$ \Delta = (b^2-4ac) = (-5)^2-4(2)(1) = 25 - 8 = 17 $$
Il discriminante è positivo Δ>0, quindi le altre soluzioni sono
$$ x = \frac{-b \pm \sqrt{ \Delta }}{2a} $$
$$ x = \frac{-(-5) \pm \sqrt{17}}{2 \cdot 2} $$
$$ x = \frac{5 \pm \sqrt{17}}{4} $$
$$ x = \begin{cases} \frac{5 - \sqrt{17}}{4} = 0,22 \\ \\ \frac{5 + \sqrt{17}}{4} = 2,28 \end{cases} $$
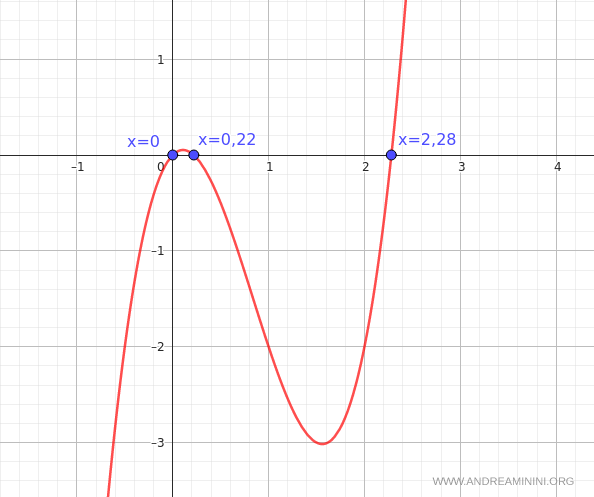
In conclusione, il polinomio iniziale 2x3 - 5x2 + x si annulla in tre punti distinti
$$ x_1 = 0 $$
$$ x_2 = 0,22 $$
$$ x_3 = 2,28 $$
In questo modo ho trovato tutte le soluzioni dell'equazione di terzo grado 2x3 - 5x2 + x=0
Verifica. Per verificare i risultati costruisco il grafico del polinomio. Il polinomio si annulla P(x)=0 effettivamente quando x=0, x=0,22 o x=2,28. In questi punti il grafico del polinomio P(x) interseca l'asse delle ascisse (y=0)
E così via.
