Il quadrato di un binomio
Il quadrato di un binomio (a+b)2 è un trinomio composto dalla somma algebrica del quadrato del primo termine (a2) e del secondo termine (b2) e dal doppio prodotto dei due termini (2ab). $$ (a+b)^2 = a^2+b^2+2ab $$
Questa formula è generale perché include anche i casi in cui uno dei termini ha segno meno.
Basta applicare la regola del segno quando si calcola il doppio prodotto (2ab).
Nota. Secondo la regola del segno del prodotto algebrico, il prodotto tra due fattori concordi (di segno uguale) è sempre positivo. Il prodotto è invece negativo se i due fattori sono discordi (di segno opposto).
Un esempio pratico
Esempio 1
Ecco un esempio di un binomio al quadrato
$$ (3a+2b)^2 $$
Espando il quadrato del binomio calcolando la somma del quadrato dei due termini e del loro doppio prodotto
$$ (3a)^2+(2b)^2+2 \cdot (3a) \cdot (2b) $$
Applico la proprietà associativa e commutativa del prodotto per moltiplicare tra loro i coefficienti e le lettere.
$$ 9a^2+4b^2+ (2 \cdot 3 \cdot 2) \cdot (a \cdot b) $$
Il risultato finale è lo stesso polinomio in forma espansa.
$$ 9a^2+4b^2+ 12ab $$
Esempio 2
Considero il caso in cui il secondo termine è negativo.
$$ (3a-2b)^2 $$
Per calcolare il quadrato del binomio applico la stessa regola iniziale.
$$ (3a)^2+(-2b)^2+2 \cdot (3a) \cdot (-2b) $$
Per la regola del segno i quadrati sono sempre positivi perché il prodotto è tra termini con lo stesso segno.
Il doppio prodotto è invece negativo perché i due termini del binomio hanno segno opposto.
$$ 9a^2+4b^2+ [2 \cdot 3 \cdot (-2)] \cdot (a \cdot b) $$
Il risultato finale è lo stesso polinomio in forma espansa.
$$ 9a^2+4b^2-12ab $$
In questo caso il doppio prodotto è negativo.
Esempio 3
Infine, considero il caso in cui entrambi i termini sono negativi
$$ (-3a-2b)^2 $$
Applico la formula del quadrato di un binomio
$$ (-3a)^2+(-2b)^2+2 \cdot (-3a) \cdot (-2b) $$
$$ 9a^2+4b^2+[2 \cdot (-3) \cdot (-2)] \cdot (a \cdot b) $$
I quadrati sono sempre termini positivi.
Anche il doppio prodotto è positivo perché i termini del binomio hanno lo stesso segno, sono entrambi negativi.
$$ 9a^2+4b^2+12ab $$
Il risultato finale è il quadrato del binomio in forma espansa.
La dimostrazione
La dimostrazione del quadrato del binomio è geometrica.
Considero due segmenti a e b di lunghezza diversa.

La somma dei due segmenti è un segmento (a+b)
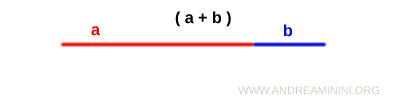
Costruisco un quadrato sul segmento (a+b)
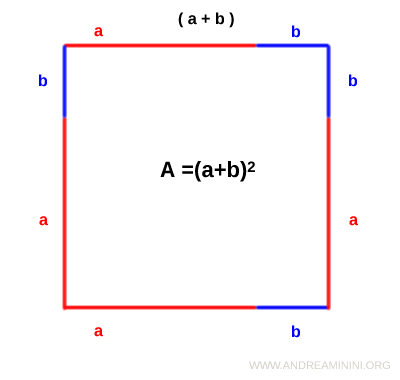
L'area del quadrato è la base per l'altezza (a+b)·(a+b) ossia un lato al quadrato (a+b)2
$$ A = (a+b) \cdot (a+b) = (a+b)^2 $$
Guardando il quadrato gli antichi greci si accorsero che è composto dall'unione di due quadrati e da due rettangoli uguali, non sovrapposti tra loro.
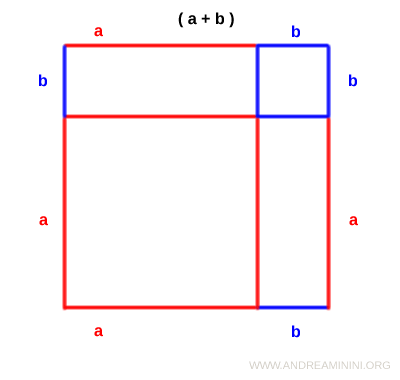
Calcolo le aree dei due quadrati e dei due rettangoli interni.
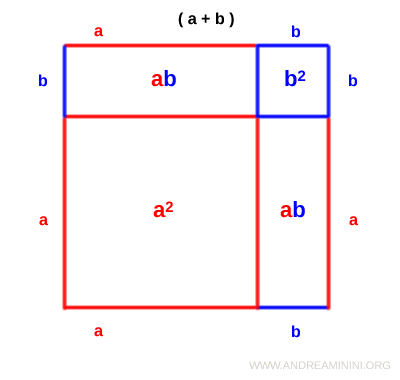
La somma delle aree dei quadrati e dei rettangoli interni a2+b2+ab+ab è uguale all'area del quadrato A=(a+b)2 che li contiene.
$$ A = (a+b)^2 = a^2 + b^2 + ab + ab $$
Sommo i due monomi simili ab e ottengo la formula del quadrato del binomio
$$ A = (a+b)^2 = a^2 + b^2 + 2ab $$
Questa dimostrazione risale a più di duemila anni fa ma, secondo me, è ancora la più efficace per capire la regola del quadrato del binomio.
E così via.
