Il prodotto tra la somma e la differenza di due monomi
Il prodotto tra la somma e la differenza di due monomi è uguale alla differenza tra il quadrato del primo monomio e il quadrato del secondo monomio. $$ (a+b) \cdot (a-b) = a^2 - b^2 $$
Un esempio pratico
Considero due polinomi P(x) e Q(x) composti dalla somma e dalla differenza dei monomi 4a e 2b
$$ P(x): \ 4a + 2b $$
$$ Q(x): \ 4a - 2b $$
Devo calcolare il prodotto tra i due polinomi
$$ P(x) \cdot Q(x) = (4a+2b) \cdot (4a-2b) $$
Per farlo applico la regola del prodotto notevole
$$ P(x) \cdot Q(x) = (4a)^2-(2b)^2 $$
Quindi, il prodotto notevole tra i due polinomi è
$$ P(x) \cdot Q(x) = 16a^2 - 4b^2 $$
La dimostrazione
Per dimostrare questo prodotto notevole utilizzo la geometria.
Considero due segmenti a e b

Disegno un rettangolo in cui la base è la somma dei segmenti (a+b) e l'altezza è la differenza dei due segmenti (a-b)
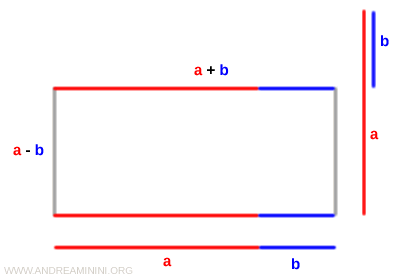
L'area di questo rettangolo è
$$ Area = (a+b) \cdot (a-b) $$
Ora divido il rettangolo in due rettangoli di pari altezza (a-b).
Il primo rettangolo ha base a mentre il secondo rettangolo ha base b.
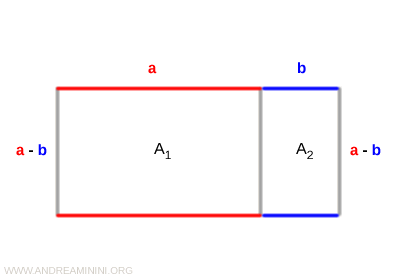
La somma delle aree A1 e A1 dei due rettangoli è uguale all'area A del rettangolo iniziale.
$$ A = A_1 + A_2 $$
Calcolo separatamente le aree dei due rettangoli
$$ A_1 = a \cdot (a-b) = a^2 -ab $$
$$ A_2 = b \cdot (a-b) = ab-b^2 $$
Quindi, la somma delle due aree è
$$ A = A_1 + A_2 $$
$$ A = (a^2 -ab) + (ab-b^2) $$
$$ A = a^2 -ab + ab-b^2 $$
Pertanto, l'area A del rettangolo iniziale è uguale alla differenza dei quadrati dei segmenti a e b
$$ A = a^2 -b^2 $$
Ho dimostrato geometricamente la regola del prodotto notevole.
Esercizi svolti
Ecco alcuni esempi di difficoltà crescente sull'identità notevole:
Esempio 1
Considero l'espressione
$$ (5x - 2) \cdot (5x + 2)$$
In questo caso riconosco subito che $ a=5x $ e $ b=2 $ e applico l'identità.
$$ (5x)^2 - (2)^2 = 25x^2 - 4 $$
Nota. Allo stesso risultato sarei giunto facendo il prodotto tra i due binomi. $$ (5x - 2) \cdot (5x + 2) = $$ $$ 5x \cdot (5x + 2) -2 \cdot (5x + 2) = $$ $$ 25x^2 + 10x - 10x -4 = $$ $$ 25x^2 -4 $$
Esempio 2
$$ (5+3x) \cdot (-3x+5)$$
Per la proprietà commutativa posso modificare l'ordine dei fattori
$$ (5+3x) \cdot (5-3x)$$
Ora riconosco l'identità $ (a+b)(a-b) $ dove $ a=5 $ e $ b=3x $.
Quindi posso applicare la formula $ (a+b)(a-b) = a^2-b^2 $ senza dover svolgere il prodotto dei binomi.
$$ (5+3x) \cdot (5-3x) = (5)^2 - (3x)^2 = 25 - 9x^2 $$
Esempio 3
Considero l'espressione
$$ \left(\sqrt{2x + 3} - \sqrt{x}\right) \cdot \left(\sqrt{2x + 3} + \sqrt{x}\right) $$
Anche in questo caso riconosco la forma $(a - b)(a + b) = a^2 - b^2 $ ponendo $a = \sqrt{2x + 3} $ e $ b = \sqrt{x}$.
$$ \left(\sqrt{2x + 3} - \sqrt{x}\right) \cdot \left(\sqrt{2x + 3} + \sqrt{x}\right) = $$
$$ ( \sqrt{2x + 3} )^2 - ( \sqrt{x} )^2 = $$
$$ 2x+3-x = $$
$$ x+3 $$
Esempio 4
Considero l'espressione
$$ (5x-2+x^2) \cdot (x^2 +5x+2) $$
Apparentemente non sembra una differenza di quadrati... ma basta riordinare i termini e raggrupparli che l'identità $ (a-b)(a+b) $ emerge.
$$ (x^2+5x-2) \cdot (x^2+5x+2) $$
$$ ((x^2+5x)-2) \cdot ((x^2+5x)+2) $$
$$ ((x^2+5x)+2) \cdot ((x^2+5x)-2) $$
In questo caso $ a=x^2+5x $ e b = 2
$$ ((x^2+5x)+2) \cdot ((x^2+5x)-2) = (x^2+5x)^2 - (2)^2 $$
$$ x^4 + 2 \cdot x^2 \cdot 5x + 25x^2 - 4 = $$
$$ x^4 + 10 \cdot x^3 + 25x^2 - 4 $$
Quindi, l’identità notevole della differenza di quadrati si applica anche a espressioni più complesse, come quelle con radici o con più termini o con termini in ordine diverso.
L’importante è saper riconoscere la struttura (a+b)(a−b), anche quando si presenta in forme meno evidenti.
E così via.
