Il prodotto tra due polinomi
Il prodotto tra due polinomi P e Q è un polinomio composto dalla somma dei prodotti di ogni termine del primo polinomio fattore P per ogni termine del secondo polinomio fattore Q.
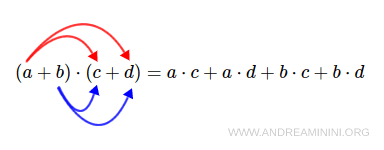
Il risultato è un polinomio prodotto di grado pari alla somma dei gradi dei polinomi.
Quanti sono i termini del polinomio prodotto?
Se il primo polinomio è formato da $ m $ termini e il secondo polinomio da $ n $ termini, il polinomio prodotto deve contenere $ m \cdot n $ termini prima della riduzione di eventuali termini simili. Dopo la riduzione dei termini simili (es. a+2a=3a) potrebbe contenerne di meno.
Quest'ultima regola è molto utile per controllare di non aver dimenticato nessun termine nella moltiplicazione.
Esempio. Considero il prodotto tra due polinomi fattori di primo grado $$ ( 2a + 3b) \cdot (3a - 4b) $$ Applico la proprietà associativa e la proprietà distributiva della moltiplicazione rispetto all'addizione $$ 2a \cdot (3a - 4b) + 3b \cdot (3a - 4b) $$ Come previsto il polinomio prodotto contiene 4 termini prima della riduzione $$ 6a^2 - 8ab + 9ab - 12b^2 $$ Infine, svolgo i calcoli per ridurre il polinomio alla forma normale $$ 6a^2 + ab - 12b^2 $$ Il risultato è un polinomio prodotto di grado due composto da tre termini.
Nel caso del prodotto di un monomio per un polinomio, basta applicare la proprietà distributiva del prodotto.
Per moltiplicare un monomio per un polinomio, si moltiplica il monomio per tutti i termini del polinomio e si sommano i prodotti ottenuti.
$$ a \cdot (a+b+c) = a \cdot a + a \cdot b + a \cdot c = a^2 +ab + ac $$
Poiché la moltiplicazione è commutativa, il risultato non cambia se il primo fattore è un polinomio e il secondo fattore è un monomio.
Esempio. Considero il prodotto tra un polinomio è un monomio $$ ( 2a + 3b) \cdot 3c $$ Anche in questo caso moltiplico ogni termine del polinomio per il monomio e sommo i prodotti $$ 2a \cdot 3c + 3b \cdot 3c = 6ac + 9bc $$ Il risultato finale è un altro polinomio di grado uno.
La dimostrazione
Per dimostrare questa regola algebrica posso ricorrere alla geometria elementare
Considero un rettangolo di base (a+b) e altezza (c+d)
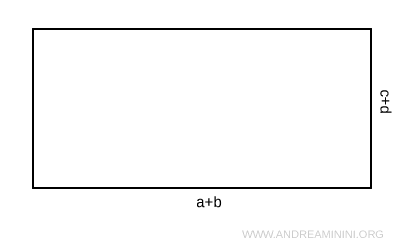
L'area A del rettangolo è uguale al prodotto tra la base e l'altezza
$$ A = (a+b) \cdot (c+d) $$
Suddivido la base del rettangolo in due segmenti distinti a e b.
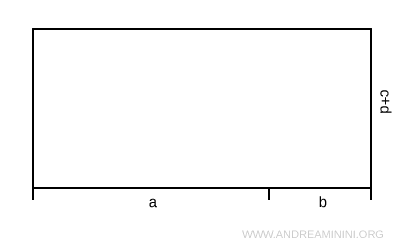
Suddivido l'altezza del rettangolo in due segmenti distinti c e d.
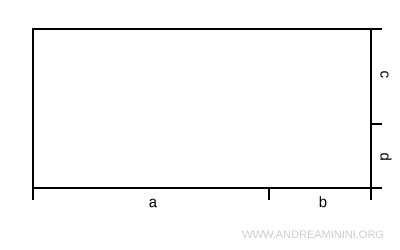
In questo modo ottengo quattro rettangoli non sovrapposti tra loro che occupano l'intera area A del rettangolo principale
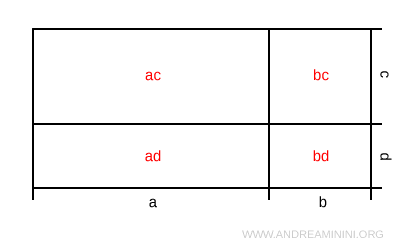
Pertanto, la somma delle aree dei quattro rettangoli è pari all'area A.
$$ A = ac + ad + bc + bd $$
In conclusione, l'area del rettangolo è uguale a
$$ A = (a+b) \cdot (c+d) = ac + ad + bc + bd $$
Questo dimostra geometricamente la regola di calcolo del prodotto tra due polinomi.
E così via.
