Il quadrato di un trinomio
Il quadrato di un trinomio (a+b+c)2 è la somma algebrica dei quadrati dei tre termini e dei doppi prodotti delle combinazioni dei termini presi a coppie di due. $$ (a+b+c)^2 = a^2+b^2+c^2+ 2ab+2ac+2bc $$
Dove $ a $, $ b $, $ c $ possono essere dei monomi o anche dei polinomi.
La formula può essere generalizzata anche per calcolare il quadrato di polinomi con più di tre termini.
$$\left(\sum_{i=1}^{n} x_i\right)^2 = \sum_{i=1}^{n} x_i^2 + 2 \sum_{1 \le i < j \le n} x_i x_j$$
In altre parole, basta sommare il quadrato di tutti i termini e il doppio prodotto di ciascuna coppia di termini presi a due a due.
Ad esempio, per calcolare il quadrato di un polinomio con quattro termini (a+b+c+d)2 posso scrivere: $$ (a+b+c+d)^2 = $$ $$ = a^2+b^2+c^2+d^2+2ab+2ac+2ad+2bc+2bd+2cd $$
Un esempio pratico
Ecco un esempio di un trinomio al quadrato
$$ (2a - 3b + 4c)^2 $$
Calcolo il quadrato applicando la regola precedente
$$ (2a - 3b + 4c)^2 = (2a)^2+(-3b)^2+(4c)^2 + 2 \cdot (2a) \cdot (-3b) + 2 \cdot (2a) \cdot (4c) + 2 \cdot (-3b) \cdot (4c) $$
$$ (2a - 3b + 4c)^2 = 4a^2+9b^2+16c^2 - 12ab + 16ac - 24 bc $$
Attenzione al segno nei doppi prodotti. Quando si calcola il quadrato di un trinomio (o più in generale, di un polinomio), bisogna fare attenzione ai segni dei termini nei doppi prodotti. Nei quadrati, il segno è sempre positivo perché $( -x )^2 = x^2$ ma nei doppi prodotti, il segno resta e fa la differenza. Ad esempio $$ (a - b)^2 = a^2 - 2ab + b^2 $$ In questo caso il doppio prodotto $ 2 \cdot a \cdot (-b) $ è uguale a $ -2ab $, quindi è negativo!
La dimostrazione
Considero il quadrato del trinomio
$$ (a+b+c)^2 $$
Applico la proprietà associativa dell'addizione
$$ [(a+b)+c]^2 $$
Ora, questo è il quadrato di un binomio considerando $ (a+b) $ come primo termine e $ c $ come secondo termine.
Quindi, applico la formula del quadrato del binomio $ (x+y)^2 = x^2+2xy+y^2 $
$$ [(a+b)+c]^2 = (a+b)^2 + 2 (a+b) c + c^2 $$
Poi sviluppo i calcoli
$$ [(a+b)+c]^2 = a^2+2ab+b^2 + 2ac+2bc + c^2 $$
Infine, applico la proprietà commutativa
$$ [(a+b)+c]^2 = a^2+b^2+ c^2+2ab + 2ac+2bc $$
Ho così ottenuto la formula che volevo dimostrare.
La dimostrazione geometrica
Posso giungere alla stessa conclusione anche seguendo un ragionamento geometrico.
Considero tre segmenti $ a $ , $ b $ , $ c $

Li dispongo uno dopo l'altro per formare i lati di un quadrato, ciascuno di lunghezza $ a+b+c $.
L'area del quadrato è uguale al lato per se stesso, quindi al prodotto $ (a+b+c) \cdot (a+b+c) $ ossia al quadrato del trinomio $ (a+b+c)^2 $
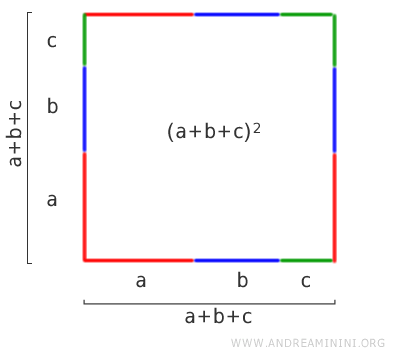
L'area del quadrato è anche uguale alla somma delle aree dei quadrati e dei rettangoli più piccoli in cui è suddiviso.
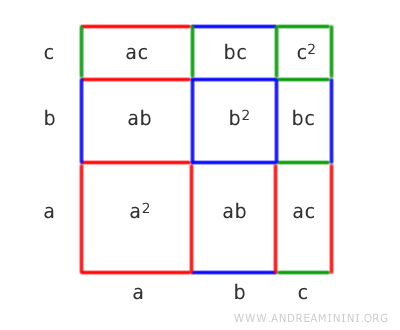
Sommando le superfici dei quadrati e dei rettangoli ottengo:
$$ a^2+b^2+ c^2+2ab + 2ac+2bc $$
Questo dimostra la formula del quadrato del trinomio.
$$ (a+b+c)^2 = a^2+b^2+ c^2+2ab + 2ac+2bc $$
Note a margine
Alcune note a margine e osservazioni
- Tecnica alternativa
Può capitare di dimenticarsi questa formula perché è meno frequente del quadrato del binomio, in particolar modo negli studi superiori. In questi casi basta trasformare il trinomio $ (a+b+c)^2 $ in questa forma equivalente $ ((a+b)+c)^2 $ $$ (a+b+c)^2 $$ $$ ((a+b)+c)^2 $$ Poi applicare la formula del binomio del quadrato $ (A+B)^2=A^2+2AB+B^2 $ considerando A=(a+b) e B=c come i termini del binomio. $$ (a+b)^2 + 2(a+b)c+c^2 $$ $$ a^2+2ab+b^2 + 2ac + 2bc+c^2 $$ $$ a^2+b^2+c^2+2ab + 2ac + 2bc $$ Il risultato finale è lo stesso.
E così via.
