Il triangolo di Tartaglia
Il triangolo di Tartaglia è una rappresentazione dei coefficienti binomiali (a+b)n.
I coefficienti binomiali sono i coefficienti del polinomio che si ottiene con lo sviluppo della potenza ennesima di un binomio (a+b)n .
Il triangolo di Tartaglia è anche conosciuto come triangolo di Pascal.
Come costruire il triangolo di Tartaglia
Si parte dal numero 1 come vertice superiore del triangolo.
Il vertice è la riga zero (n=0).
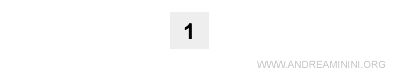
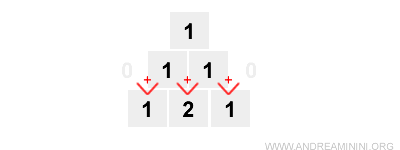
Ogni numero seguente del triangolo è uguale alla somma dei numeri adiacenti nella riga precedente. Gli spazi vuoti sono considerati nulli.
Seguendo queste regole aggiungo la prima riga (n=1).
Nota. I numeri della prima riga (n=1) sono i coefficienti dello sviluppo del binomio (a+b) elevato a 1. $$ (a+b)^1 = a+b $$ I coefficienti di a e b sono rispettivamente 1 e 1.
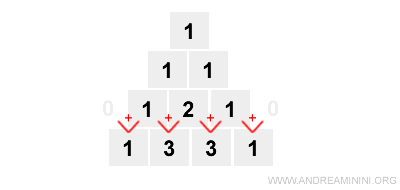
Applico le stesse regole per scrivere la seconda riga (n=2).
Nota. I numeri della seconda riga (n=1) sono i coefficienti dello sviluppo del binomio (a+b) elevato a 2. $$ (a+b)^2 = a^2+2ab+b^2 $$ I coefficienti dei termini sono 1,2,1 ossia 1a2+2ab+1b2
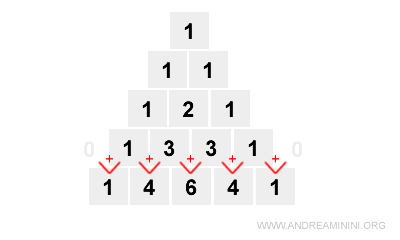
Poi costruisco la terza riga
Nota. I numeri della terza riga (n=3) sono i coefficienti dello sviluppo del binomio (a+b) elevato a 3. $$ (a+b)^3 = a^3+3a^2b+3ab^2+b^3 $$ I coefficienti dei termini sono 1,3,3,1 ossia 1a3+3a2+3ab2+1b3
Poi la terza riga (n=3)
Nota. I numeri della quarta riga (n=4) sono i coefficienti del polinomio che si ottiene sviluppando la potenza del binomio (a+b)4. $$ (a+b)^4 = a^4+4a^3b+6a^2b^2+4ab^3+b^4 $$ I coefficienti del polinomio sono 1,4,6,4,1 ossia 1a4+4a3b+6a2b2+4ab3+1b4
Con lo stesso metodo costruisco le altre righe per n tendente a infinito.
Non c'è alcun limite alla grandezza del triangolo di Tartaglia.
Le combinazioni e il triangolo di Tartaglia
Ogni numero del triangolo è uguale alla combinazione C(n,k). $$ C(n,k)= \begin{pmatrix} n \\ k \end{pmatrix} $$
Dove n è il numero di riga dell'elemento e k è la posizione dell'elemento nella riga.
Nota. Sia n che k partono da zero. Quindi, la prima riga è n=0, la prima posizione sulla riga è k=0. E via dicendo.
Esempio
Il numero 10 si trova sulla riga n=5 alla posizione k=2.
Ora calcolo le combinazioni semplici C(5,2).
$$ \begin{pmatrix} 5 \\ 2 \end{pmatrix} = \frac{5!}{2!(5-2)!} = \frac{120}{12} = 10 $$
Il numero delle combinazioni di classe k=2 di un insieme con n=5 elementi è uguale a 10.
Ho così dimostrato l'uguaglianza tra ogni numero del triangolo di Tartaglia e il calcolo combinatorio.
E così via.
