Il teorema del resto
In una divisione tra polinomi del tipo $$ \frac{P(x)}{x-k}=Q(x)+R $$ il resto R della divisione è uguale al valore che assume il polinomio P(x) quando x=k $$ P(k)=R $$ Dove k è il termine noto del polinomio divisore scritto nella forma (x-k).
E' una proprietà generale della divisione di un polinomio per (x-k)
Questo teorema mi permette di calcolare il resto della divisione senza doverla calcolare.
Attenzione. Vale solo per le divisioni in cui il polinomio al denominatore è (x-k). Quindi, non è una regola generale per tutte le divisioni tra polinomi.
Un esempio pratico
Devo calcolare la divisione tra due polinomi
$$ \frac{x^2+5x+7}{x+3} $$
Svolgo la divisione
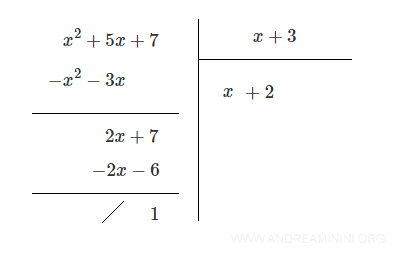
Il risultato della divisione è il polinomio quoziente Q(x)=x+2 e un resto R=1
$$ \frac{x^2+5x+7}{x+3} = x+2 \ \ \ \ \text{con resto R=1} $$
In base al teorema del resto, il polinomio al numeratore assume il valore P(x)=R quando x=k
$$ P(x)=R \ \ \ \ \text{con x=k} $$
In questo caso però il polinomio divisore è (x+1).
Per applicare il teorema del resto devo scriverlo in modo equivalente nella forma (x-k) con il segno meno
$$ (x-(-1))=(x+1) $$
Quindi, il termine noto del divisore che devo considerare nel teorema del resto è k=-1
$$ P(-1) \ \ \ \ \text{con x=-1} $$
$$ P(-1): \ x^2+5x+7 $$
$$ P(-1): \ (-1)^2+(-1) \cdot 5+7 $$
$$ P(-1): \ -1 + - 5+7 $$
$$ P(-1): \ 1 $$
Il valore del polinomio P(-1)=1 è uguale al resto R=1 della divisione tra i due polinomi.
La dimostrazione
La dimostrazione del teorema del resto è molto semplice.
Considero la divisione tra il generico polinomio P(x) e il polinomio (x-k)
$$ \frac{P(x)}{x-k}=Q(x) \ \ \ \text{con resto R} $$
Applico la proprietà invariantiva delle equazioni e moltiplico entrambi i membri delle equazioni per (x-k)
$$ \frac{P(x)}{x-k} \cdot (x-k) =Q(x) \cdot (x-k) \ \ \ \text{con resto R} $$
Poi semplifico il membro di sinistra
$$ P(x) =Q(x) \cdot (x-k) \ \ \ \text{con resto R} $$
Ora sostituisco x=k
$$ P(k) =Q(k) \cdot (k-k) \ \ \ \text{con resto R} $$
Poiché k-k=0 il prodotto nel membro di destra si annulla.
$$ P(k) =Q(k) \cdot 0 \ \ \ \text{con resto R} $$
$$ P(k) =0 \ \ \ \text{con resto R} $$
$$ P(k) = R $$
Questo dimostra il teorema del resto.
E così via.
