Le relazioni d'ordine

Le relazioni d'ordine sono relazioni matematiche che soddisfano la proprietà riflessiva, antisimmetrica e transitiva.


• Proprietà riflessiva $$ \forall \ a \in A \:\: aρa $$
• Proprietà antisimmetrica $$ \forall \ a,b \in A \ , \ aρb , \ a \ne b \Rightarrow b \require{cancel} \cancel{ρ} a $$
• Proprietà transitiva $$ \forall \ a,b,c \in A :\: [ aρb ∧ bρc ] \rightarrow aρc $$

Questa definizione è anche detta relazione d'ordine largo.

Esiste anche un'altra definizione di relazione d'ordine, detta relazione d'ordine stretto in cui la proprietà riflessiva è sostituita con la proprietà antiriflessiva.

Pertanto. In generale si considerano relazioni d'ordine tutte le relazioni che sono riflessive (o antiriflessive), antisimmetriche e transitive

Un esempio pratico

Considero l'insieme dei numeri naturali N

$$ N = \{ 1, 2, 3, 4, ... \} $$

Devo capire se la relazione R : "x è multiplo di y" è una relazione di ordine.

Per farlo verifico se soddisfa le tre proprietà delle relazioni d'ordine.

• La relazione R è riflessiva perché ogni numero è multiplo di se stesso se lo moltiplico per il fattore 1.
• La relazione R è antisimmetrica perché, presi due numeri diversi, se x è multiplo di y allora y non è multiplo di x.
• La relazione R è transitiva perché, presi tre numeri diversi, se x è multiplo di y e y è multiplo di z, allora x è multiplo di z.

La relazione soddisfa le tre proprietà delle relazioni d'ordine.

Pertanto, la relazione R è una relazione d'ordine.

La differenza tra relazioni di ordine largo e stretto

Esistono due tipi di relazioni d'ordine

• Le relazioni di ordine largo
  Sono le relazioni che soddisfano la proprietà riflessiva, antisimmetrica e transitiva.

  Esempio. La relazione "x è multiplo di y" è una relazione di ordine largo perché è riflessiva. Ogni numero è multiplo di se stesso per il fattore 1, quindi soddisfa la proprietà riflessiva (es. 2·1=2, 3·1=3, ecc.) oltre a soddisfare la proprietà antisimmetrica e transitiva.

• Le relazioni di ordine stretto
  Sono le relazioni che soddisfano la proprietà antiriflessiva, antisimmetrica e transitiva.

  Esempio. La relazione "x è più alto di y" è una relazione di ordine stretto perché è antiriflessiva. Nessuna persona può essere più alta di se stessa, quindi la relazione soddisfa la proprietà antiriflessiva oltre a soddisfare la proprietà antisimmetrica e transitiva.

In pratica, le relazioni di ordine stretto sono antiriflessive mentre quelle di ordine largo sono riflessive.

Le relazioni d'ordine totali e parziali

Le relazioni d'ordine largo o stretto sono distinte anche in base alla loro capacità di ordinare un insieme. Una relazione d'ordine può essere totale o parziale

• Una relazione d'ordine parziale

  Le relazioni d'ordine parziale mettono in relazione solo una parte degli elementi dell'insieme ma non tutti. In questi casi non è sempre possibile confrontare tutti gli elementi tra loro.

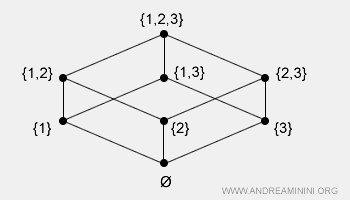
  Si applica soltanto in un sottoinsieme di coppie (a,b) dell'insieme. In questo caso l'insieme degli elementi è detto insieme parzialmente ordinato. In un insieme parzialmente ordinato soltanto alcune coppie di elementi del prodotto cartesiano sono confrontabili tra loro.

  Esempio. L'insieme delle parti P(X) con X={1,2,3} è composto dai seguenti elementi: { Ø {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3} }. Si tratta di un insieme parzialmente ordinato rispetto alla relazione di inclusione ⊆ perché soltanto alcune coppie sono confrontabili: {1}⊆{1,2} ma {3} ⊈ {1,2}. E così via. La rappresentazione grafica della relazione è la seguente:
  

• Una relazione d'ordine totale

  Le relazioni d'ordine totale mettono in relazione tutti gli elementi dell'insieme. In questo caso è sempre possibile confrontare ogni elemento con tutti gli altri.

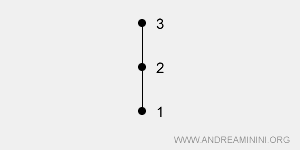
  Si applica su tutte le coppie (a,b) dell'insieme. In questo caso l'insieme degli elementi è detto insieme totalmente ordinato o catena. Sono dette catene perché hanno una struttura verticale. Tutte le coppie dell'insieme sono confrontabili tra loro.

  Esempio. Lo stesso insieme precedente X={1,2,3} è un ordinamento totale nei confronti della relazione di minoranza ≤ ( oppure di maggioranza ≥ ). In questo caso è possibile mettere in relazione qualsiasi coppia di elementi tra loro. Ad esempio, 1ρ3, 1ρ2, 2ρ3. La rappresentazione grafica prende la forma di una catena perché ogni elemento è direttamente confrontabile con gli altri elementi dell'insieme.
  

 

Come rappresentare graficamente una relazione d'ordine

Le relazioni d'ordine di un insieme X sono rappresentabili graficamente tramite punti e linee.

Ogni punto è associato a un elemento dell'insieme X.

Il segmento che unisce due punti individua due elementi direttamente confrontabili tra loro tramite la relazione d'ordine senza elementi intermedi.

Esempio. Gli elementi 1 e 3 sono confrontabili tra loro tramite la relazione di minoranza (≤). Tuttavia, tra loro c'è anche l'elemento 2. Per questa ragione i punti 1 e 3 non sono uniti da una linea. Sono invece collegati da una linea i punti 1 e 2 perché non c'è nessun elemento intermedio. Lo stesso si può dire per gli elementi 2 e 3.

Insiemi ordinati isomorfi

Due insiemi ordinati sono isomorfi se hanno la stessa struttura relazionale.

Ad esempio, gli insiemi totalmente ordinati con lo stesso numero n di elementi (cardinalità) sono sempre isomorfi.

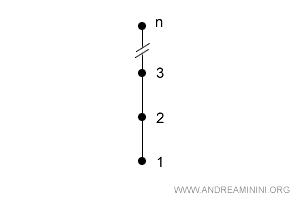
In pratica, negli insiemi isomorfi le relazioni tra gli elementi hanno la stessa forma.

E così via.