Cos'è un reticolo
Un reticolo è un insieme parzialmente ordinato A in cui gli elementi, presi a coppia di due (x,y), formano un sottoinsieme B con un estremo inferiore e superiore.
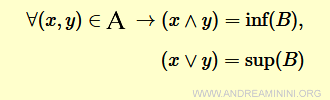
Dove
- L'estremo inferiore è il massimo dei minoranti del sottoinsieme B.
E' detto intersezione e si indica con $$ x ∧ y \:\: = \:\: inf(x,y) $$
- L'estremo superiore è il minimo dei maggioranti del sottoinsieme B.
E' detto unione e si indica con $$ x ∨ y \:\: = \:\: sup(x,y) $$
Un esempio di reticolo
In questa figura ho disegnato due insiemi parzialmente ordinati (A,≥).
Uno è un reticolo e l'altro no.
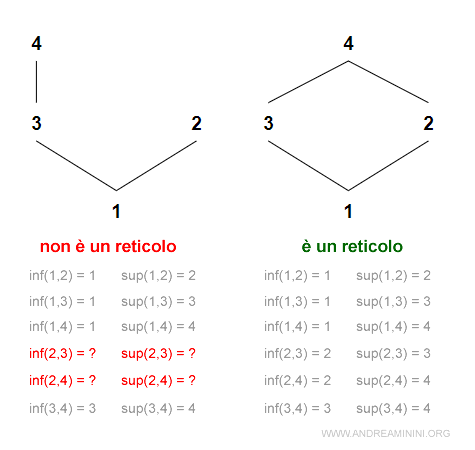
Nel primo insieme parzialmente ordinato mancano le relazioni inf() e sup() tra le coppie di elementi (2,3) e (2,4).
Nel secondo insieme, invece, tutte le coppie del prodotto cartesiano dei due insiemi hanno una relazione di inferiorità e superiorità.
Il secondo insieme è un reticolo.
Altri esempi pratici di reticoli
Il reticolo algebrico
Il reticolo algebrico (L,∧,∨) è un reticolo in cui sono definite due operazioni binarie ∧ e ∨ dette, rispettivamente, intersezione ( moltiplicazione ) e unione ( addizione ).
In un reticolo sono definite due operazioni con i simboli
- ∧ detta "e" ( and o congiunzione )
- ∨ detta "o" ( or o disgiunzione )
Le operazioni del reticolo devono sempre soddisfare queste proprietà per ogni coppia di elementi (x,y) dell'insieme parzialmente ordinato.
- commutatività
$$ x ∧ y = y ∧ x $$ $$ x ∨ y = y ∨ x $$
- associatività
$$ x ∧ ( y ∧ z ) =( x ∧ y ) ∧ z $$ $$ x ∨ ( y ∨ z ) = ( y ∨ x ) ∨ z $$
- assorbimento
$$ x ∧ ( x ∨ y ) =x $$ $$ x ∨ ( x ∧ y ) = x $$
- idempotenza
$$ x ∧ x =x $$ $$ x ∨ x = x $$
Nota. Le prime due proprietà sono comuni nella matematica. Le ultime due, invece, sono peculiari dei reticoli. Inoltre, nei reticoli manca la proprietà distributiva.
Esempio
Definisco un insieme composto soltanto da due parti a e b.
$$ L = \{ a , b \} $$
Dal punto di vista grafico
Le operazioni sono:
- ∧ = ⋂ ( intersezione )
- ∨ = ∪ ( unione )
Devo capire se l'insieme (L,⊆) è un reticolo.
Per farlo devo verificare se soddisfa le quattro leggi dei reticoli.
Commutatività
Dati due elementi a e b
$$ a ∪ b = b ∪ a $$
$$ a \cap b = b \cap a $$
Entrambe le proprietà sono soddisfatte.
Associatività
Dati tre elementi a, b, c
$$ a ∪ ( b ∪ c ) = ( a ∪ b ) ∪ c $$
$$ a \cap ( b \cap c ) = ( a \cap b ) \cap c $$
Entrambe le proprietà sono soddisfatte.
Assorbimento
Dati due elementI
$$ a ∪ ( a \cap b ) = a $$
$$ a \cap ( a ∪ b ) = a $$
Entrambe le proprietà sono soddisfatte.
Idempotenza
Dato un elemento qualsiasi
$$ a ∪ a = a $$
$$ a \cap a = a $$
Entrambe le proprietà sono soddisfatte.
Tutte le proprietà sono soddisfatte.
Pertanto, l'insieme delle parti è un reticolo.
Come capire se un insieme parzialmente ordinato è un reticolo
Per capire se un insieme parzialmente ordinato è un reticolo, devo verificare se l'insieme (A,r) soddisfa le proprietà dei reticoli.
Esempio 1
Ho un insieme A e una relazione di divisibilità indicata con il simbolo |
$$ ( A=\{1,2,3,4,5,6,7,12 \} , | ) $$
Le operazioni sono due
- ∧ = MCD ( Massimo Comune Divisore )
- ∨ = mcm ( minimo comune multiplo )
Devo verificare se l'insieme parzialmente ordinato (A,|) è un reticolo oppure no.
Dati due elementi qualsiasi (a,b) è un reticolo se esiste sempre un estremo inferiore e superiore appartenente ad A.
$$ \forall (a,b) \rightarrow \inf(a,b) $$
$$ \forall (a,b) \rightarrow \sup(a,b) $$
Prendo due elementi qualsiasi (4,6)
$$ 4∧6 = MCD(4,6) = 2 \in A $$
$$ 4∨6 = mcm(4,6) = 12 \in A $$
Entrambi i rusultati appartengono all'insieme.
Prendo altri due elementi (2,5)
$$ 2∧5 = MCD(2,5) = 1 \in A $$
$$ 2∨5 = mcm(2,5) = 10 \notin A $$
In questo caso l'estremo superiore sup(2,5)=10 non è compreso nell'insieme A.
Pertanto, l'insieme (A,|) non è un reticolo.
Esempio 2
Ho un insieme A e una relazione di divisibilità indicata con il simbolo |
$$ ( A=\{1,2,3,6,12 \} , | ) $$
Le operazioni sono due
- ∧ = MCD ( Massimo Comune Divisore )
- ∨ = mcm ( minimo comune multiplo )
In questo caso si tratta di un reticolo.
Tutte le coppie soddisfano le relazioni x∧y e x∨y.
| ( x , y ) | MCD | mcm |
|---|---|---|
| ( 1 , 2 ) | 1 | 2 |
| ( 1 , 3 ) | 1 | 3 |
| ( 1 , 6 ) | 1 | 6 |
| ( 1 , 12 ) | 1 | 12 |
| ( 2 , 3 ) | 1 | 6 |
| ( 2 , 6 ) | 2 | 6 |
| ( 2 , 12 ) | 2 | 12 |
| ( 3 , 6 ) | 3 | 6 |
| ( 3 , 12 ) | 3 | 12 |
Esempio 3
Aggiungo un elemento (9) all'insieme precedente
$$ ( A=\{1,2,3,9,6,12 \} , | ) $$
In questo caso non è più un reticolo perché manca l'estremo sup(2,9)=18.
Il numero 18 non fa parte dell'insieme A.
| ( x , y ) | MCD | mcm |
|---|---|---|
| ( 1 , 2 ) | 1 | 2 |
| ( 1 , 3 ) | 1 | 3 |
| ( 1 , 9 ) | 1 | 9 |
| ( 1 , 6 ) | 1 | 6 |
| ( 1 , 12 ) | 1 | 12 |
| ( 2 , 3 ) | 1 | 6 |
| ( 2 , 9 ) | 1 | 18 |
| ( 2 , 6 ) | 2 | 6 |
| ( 2 , 12 ) | 2 | 12 |
| ( 3 , 9 ) | 3 | 9 |
| ( 3 , 6 ) | 3 | 6 |
| ( 3 , 12 ) | 3 | 12 |
Esempio 4
Aggiungo anche gli elementi 18 e 36 all'insieme precedente
$$ ( A=\{1,2,3,9,6,12, 18, 36 \} , | ) $$
Ora l'insieme è di nuovo un reticolo.
| ( x , y ) | MCD | mcm |
|---|---|---|
| ( 1 , 2 ) | 1 | 2 |
| ( 1 , 3 ) | 1 | 3 |
| ( 1 , 6 ) | 1 | 6 |
| ( 1 , 9 ) | 1 | 9 |
| ( 1 , 12 ) | 1 | 12 |
| ( 1 , 18 ) | 1 | 18 |
| ( 1 , 36 ) | 1 | 36 |
| ( 2 , 3 ) | 1 | 6 |
| ( 2 , 6 ) | 2 | 6 |
| ( 2 , 9 ) | 1 | 18 |
| ( 2 , 12 ) | 2 | 12 |
| ( 2 , 18 ) | 2 | 18 |
| ( 2 , 36 ) | 2 | 36 |
| ( 3 , 6 ) | 3 | 6 |
| ( 3 , 9 ) | 3 | 9 |
| ( 3 , 12 ) | 3 | 12 |
| ( 3 , 18 ) | 3 | 18 |
| ( 3 , 36 ) | 3 | 36 |
| ( 6 , 9 ) | 3 | 18 |
| ( 6 , 12 ) | 6 | 12 |
| ( 6 , 18 ) | 6 | 18 |
| ( 6 , 36 ) | 6 | 36 |
| ( 9 , 12 ) | 3 | 36 |
| ( 9 , 18 ) | 9 | 18 |
| ( 9 , 36 ) | 9 | 36 |
| ( 12 , 18 ) | 6 | 36 |
| ( 12 , 36 ) | 12 | 36 |
| ( 18 , 36 ) | 18 | 36 |
Il sottoreticolo
Un sottoreticolo è un sottoinsieme L' del reticolo L(A,≥) se per ogni coppia x,y ∈ L' , le operazioni x∧y e x∨y fanno parte del reticolo L. $$ \forall x,y \in L' \rightarrow x ∧ y \in L , x ∧ y \in L $$
Esempio
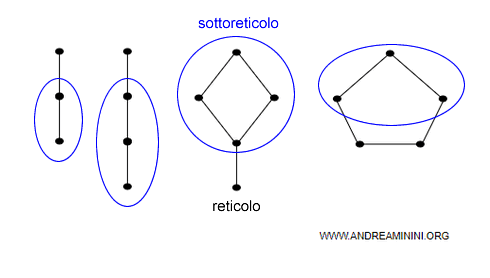
Esempio
Ho tre insiemi parzialmente ordinati
$$ A={a,b,c,d,e,f} $$
$$ B={a,c,d,f} $$
$$ C={b,c,d,e} $$
Il diagramma di Hasse degli insiemi è
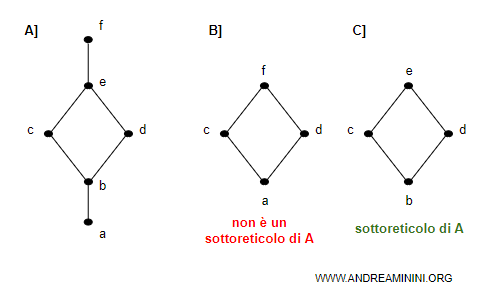
Il sottoinsieme B non è un sottoreticolo di A perché l'estremo inferiore inf(c,d) di B è diverso da inf(c,d) di A
$$ A] \:\: c ∧ d = b $$
$$ B] \:\: c ∧ d = a $$
Pertanto, il sottoinsieme B non è un sottoreticolo di A.
Nota. Pur non essendo un sottoreticolo di A, l'insieme B è comunque un reticolo perché per qualsiasi coppia di elementi esiste un estremo inferiore e superiore.
Il sottoinsieme C è invece un sottoreticolo di A perché tutti gli estremi inferiori e superiori di C coincidono con A.
Omomorfismo e isomorfismo di reticoli
Un omomorfismo di reticoli è un'applicazione A che lega un reticolo (L,≤) a un altro reticolo (L',≤). $$ A: L \rightarrow L' $$ tale che per ogni coppia x,y di L $$ A(x∧y)=A(x)∧A(y) \\ A(x∨y)=A(x)∨A(y) $$
Un esempio pratico di omomorfismo
Ho un'applicazione A che calcola la potenza.
$$ A: x \in L \rightarrow x^2 \in L' $$
Pertanto, se il reticolo L è il seguente
$$ ( A=\{1,2,3,6,12 \} , | ) $$
Nota. So già che si tratta di un reticolo dagli esempi precedenti.
L'applicazione A crea un secondo reticolo L' con la potenza degli elementi del primo
$$ ( A=\{1,4,9,36,144 \} , | ) $$
Tra il reticolo L e L' c'è una relazione.
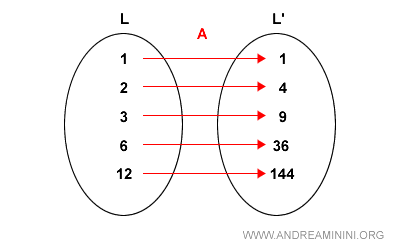
Ovviamente, non è detto che la relazione crei un altro reticolo.
Devo verificare che L' sia effettivamente un reticolo.
| ( x , y ) | x∧y | x∨y |
|---|---|---|
| ( 1 , 4 ) | 1 | 4 |
| ( 1 , 9 ) | 1 | 9 |
| ( 1 , 36 ) | 1 | 36 |
| ( 1 , 144 ) | 1 | 144 |
| ( 4 , 9 ) | 1 | 36 |
| ( 4 , 36 ) | 4 | 36 |
| ( 4 , 144 ) | 4 | 144 |
| ( 9 , 36 ) | 9 | 36 |
| ( 9 , 144 ) | 9 | 144 |
| ( 36 , 144 ) | 36 | 144 |
Per ogni elemento (x,y) esiste un estremo inferiore (x∧y) e superiore (x∨y) di L'.
Quindi L' è un reticolo e l'applicazione A è un omomorfismo.
Un isomorfismo di reticoli è un omomorfismo biettivo $$ A: L \rightarrow L' $$ $$ A^{-1}: L' \rightarrow L $$
Un esempio di isomorfismo di reticoli
L'applicazione precedente calcola la potenza degli elementi
$$ A: x \in L \rightarrow x^2 \in L' $$
So già che L e L' sono reticoli.
Posso fare l'applicazione inversa A-1 usando la radice quadrata.
$$ A^{-1}: x \in L' \rightarrow \sqrt{x} \in L $$
Quindi l'applicazione è anche biettiva oltre a essere un omomorfismo.
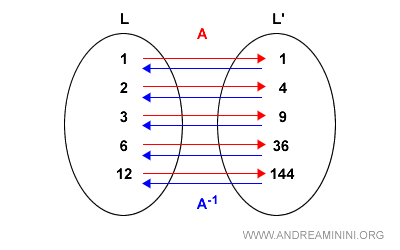
Si tratta pertanto di un isomorfismo.
E così via.
