Teorema delle perpendicolari di una retta nello spazio

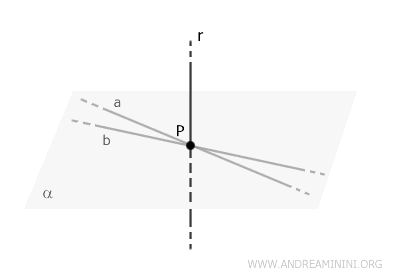
Nello spazio tutte le rette perpendicolari a una retta $ r $ che passano per un suo punto $ P \in r $ appartengono a un unico piano $ \alpha $.

La dimostrazione

Per dimostrare che tutte le rette perpendicolari a \( r \) passanti per \( P \) stanno nello stesso piano, utilizzo un ragionamento per assurdo che porterà a una contraddizione.

Considero due rette \( a \) e \( b \), entrambe perpendicolari a \( r \) e passanti per \( P \).

Queste rette determinano un piano, che chiamo \( \alpha \), anch'esso perpendicolare alla retta $ r $.  Quindi, \( \alpha \) è il piano che contiene \( a \) e \( b \).

Suppongo per assurdo il contrario del teorema, cioé che esista una retta \( t \) perpendicolare a \( r \) e passante per \( P \),  che non appartenga al piano \( \alpha \).

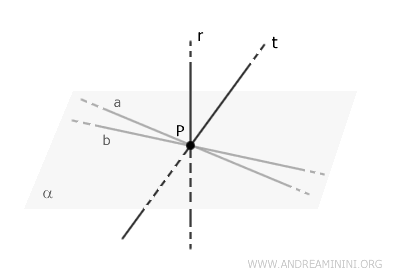
Se la retta \( t \) non è nel piano \( \alpha \), allora deve esistere un altro piano \( \beta \) che è definito dalle rette \( t \) e \( r \).

Quindi, \( \beta \) è il piano che contiene \( r \) e \( t \).

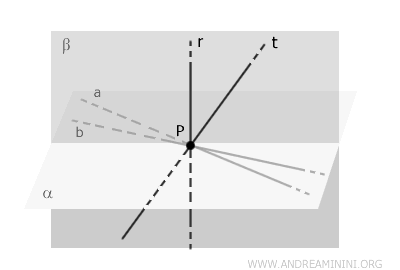
I piani \( \alpha \) e \( \beta \) si intersecano lungo una retta \( s \) che passa per il punto \( P \) perché sia \( \alpha \) che \( \beta \) contengono \( P \).

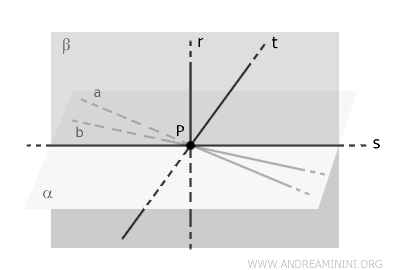
Questo ragionamento porta però a una contraddizione.

La retta \( s \) è l’intersezione dei piani \( \alpha \) e \( \beta \), quindi appartiene a entrambi i piani.

Poiché la retta \( s \) appartiene al piano \( \alpha \) che è definito da due rette  \(a \) e \( b \) perpendicolari a \( r \), per il teorema delle perpendicolari deduco che anche \( s \) è perpendicolare a \( r \).

Ora nel piano \( \beta \) ci sono due rette (\( t \) (per ipotesi) e \( s \)) (per costruzione) perpendicolari a \( r \) e passanti per \( P \). Ma questo è impossibile perché in un singolo piano una retta può avere una sola perpendicolare passante in un punto.

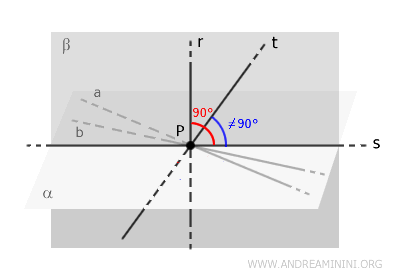
Quindi, nel piano \( \beta \), a cui appartiene anche la retta \( r \), non possono esserci due rette perpendicolari a \( r \) passanti per il punto \( P \).

Poiché l’ipotesi che la retta \( t \) non appartenga al piano \( \alpha \) porta a una contraddizione, deduco che sia vero il contrario, ovvero che \( t \) deve giacere nel piano \( \alpha \).

Questo dimostra che tutte le rette perpendicolari alla retta \( r \) e passanti in un suo punto \( P \) si trovano nello stesso piano \( \alpha \).

E con questo ho dimostrato il teorema.

E così via.