Teorema delle rette perpendicolari
Se da un punto \( P \) appartenente a una retta \( r \) si tracciano due rette \( a \) e \( b \) perpendicolari a \( r \), allora \( r \) risulta perpendicolare a qualsiasi altra retta \( s \) che passa per \( P \) e giace sul piano \( \alpha \) individuato dalle rette \( a \) e \( b \).
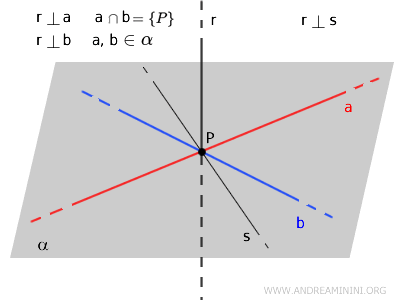
Il teorema delle tre perpendicolari è utile principalmente nella geometria nello spazio (tridimensionale) per stabilire relazioni di ortogonalità tra rette e piani.
Ad esempio, mi fornisce un criterio per verificare se una retta è perpendicolare a un'altra retta o a un piano, sfruttando la relazione tra rette e i loro piani.
La dimostrazione
Considero un punto $ P $ e una retta $ r $.
Poi traccio due rette $ a $ e $ b $ perpendicolari alla retta $ r $ che passano per il punto $ P $.
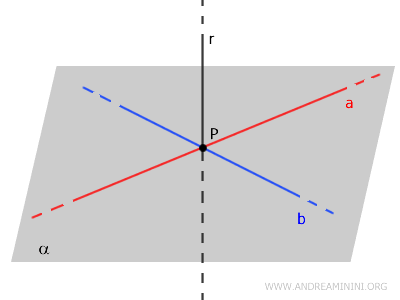
Le due rette $ a $ e $ b $ definiscono il piano $ \alpha $, quindi sono complanari.
Per costruzione le due rette $ a $ e $ b $ sono anche incidenti nel punto $ P $ e perpendicolari alla retta $ r $.
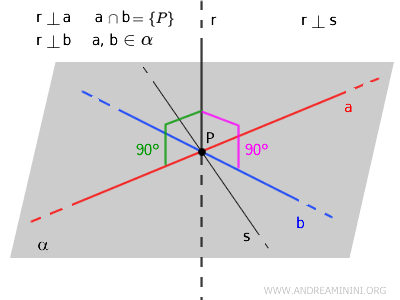
$$ a \cap b = \{ P \} $$
$$ a, b \in \alpha $$
$$ a , b \perp r $$
Quindi, la retta $ r $ è perpendicolare al piano $ \alpha $ con cui ha in comune solo il punto $ P $
$$ r \cap \alpha = \{ P \} $$
Prendo due punti $ Q $ e $ R $ sulla retta $ r $ alla stessa distanza dal punto $ P $ nei due semispazi opposti rispetto al piano $ \alpha $.
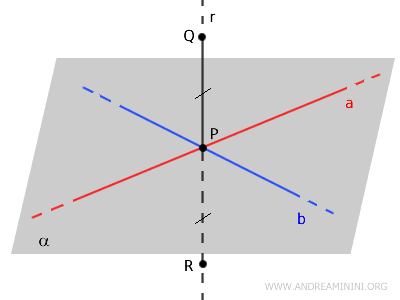
Poiché i punti Q e R sono equidistanti dal punto P, deduco che i segmenti PQ e PR sono congruenti
$$ PQ \cong PR $$
Traccio una retta $ s $ appartenente al piano $ \alpha $.
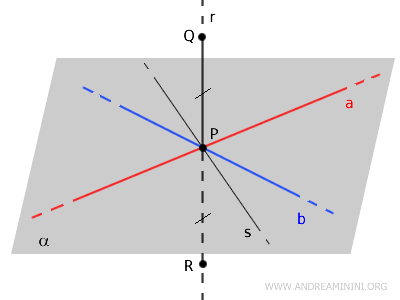
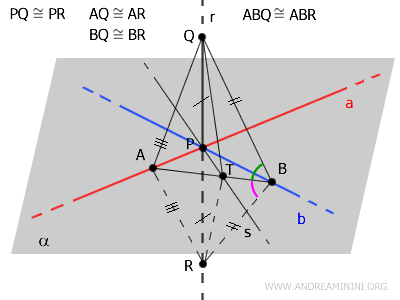
Prendo due punti $ A $ e $ B $ rispettivamente sulle rette $ a $ e $ b $ e traccio un segmento $ AB $ che interseca la retta $ s $ nel punto $ T $
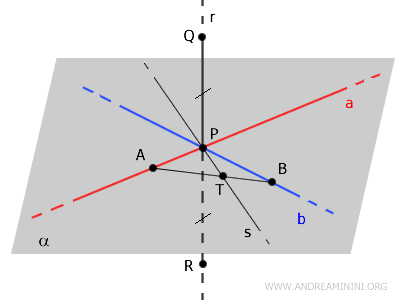
Traccio dei segmenti tra i punti AQ, TQ, BQ e AR, TR, BR ottenendo diversi triangoli.
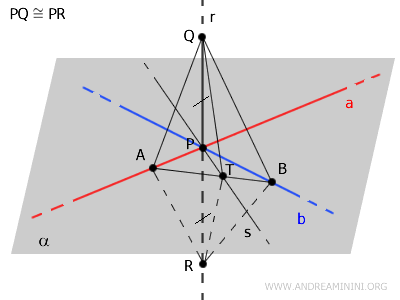
Nel triangolo AQR il segmento AP è sia l'altezza che la mediana del triangolo rispetto alla base QR poiché PQ≅PR.
Da questo deduco che il triangolo AQR è un triangolo isoscele, quindi i segmenti AQ e AR sono congruenti.
$$ PQ \cong PR $$
Allo stesso modo, anche il triangolo BQR è un triangolo isoscele perché il segmento PB è sia altezza che mediana del triangolo rispetto alla base QR.
Quindi, i segmenti BQ e BR sono congruenti tra loro.
$$ BQ \cong BR $$
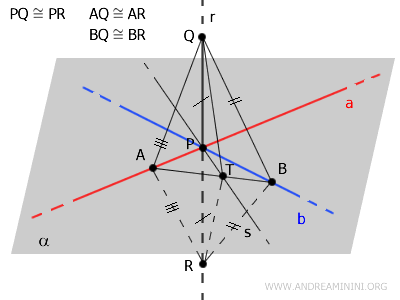
Ora dedico attenzione ai triangoli ABQ e ABR.
Secondo il terzo criterio di congruenza dei triangoli, ABQ e ABR sono congruenti perché hanno un lato coincidente AB e due i lati congruenti AQ≅AR e BQ≅BR.
$$ ABQ \cong ABR $$
Essendo congruenti, hanno anche gli angoli congruenti nello stesso ordine.
In particolar modo mi interessa sapere che gli angoli $ A\hat{B}Q $ e $ A\hat{B}R $ sono congruenti.
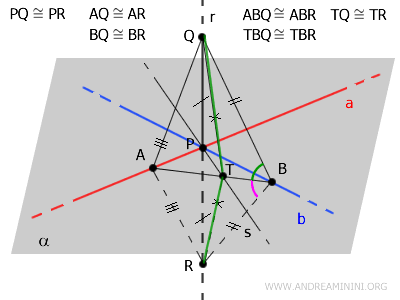
I triangoli TBQ e TBR hanno un lato coincidente TB e un lato congruente BQ≅BR con l'angolo tra di questi congruente $ ABQ \cong ABR $.
Quindi, in base al primo criterio di congruenza dei triangoli, anche i triangoli TBQ e TBR sono congruenti.
$$ TBQ \cong TBR $$
Essendo congruenti, i due triangoli TBQ e TBR hanno tutti i lati congruenti.
In particolar modo, mi interessa sapere che i segmenti TQ e TR sono congruenti.
$$ TQ \cong TR $$
Sapendo che TQ≅TR sono segmenti congruenti, deduco che il triangolo TQR è isoscele.
Quindi, il segmento PT è anche l'altezza del triangolo TQR oltre a essere la sua mediana.
Questo significa che il segmento PT è perpendicolare alla base QR ovvero forma un angolo di 90°.
$$ PT \perp QR $$
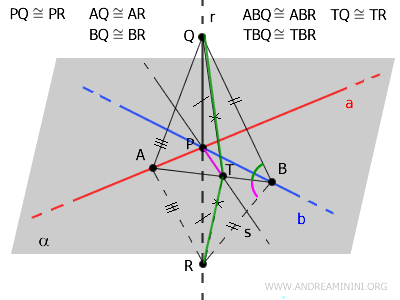
A questo punto, poiché QR è un segmento della retta $ r $ e PT è un segmento della retta $ s $, posso dedurre che le rette $ r $ e $ s $ sono perpendicolari.
$$ r \perp s $$
Questo ragionamento posso ripeterlo con qualsiasi altra retta $ s $ sul piano $ \alpha $.

Ho così dimostrato il teorema.
E così via.
