Il teorema della retta perpendicolare a due piani

Se una retta $ r $ è perpendicolare a due piani $ \alpha $ e $ \beta $ rispettivamente nei punti $ P $ e $ Q $ (due punti distinti sulla retta), allora i due piani $ \alpha $ e $ \beta $ sono paralleli $ \alpha \parallel \beta $.
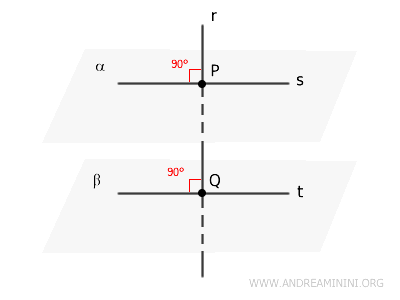
dimostrazione

Questo teorema della geometria solida è molto utile per studiare le relazioni tra rette e piani nello spazio tridimensionale.

La dimostrazione

Considero una retta $ r $ che interseca i piani $ \alpha $ e $ \beta $ rispettivamente nei punti $ P $ e $ Q $.

Per ipotesi iniziale la retta $ r $ è perpendicolare a $ \alpha $ e $ \beta $.

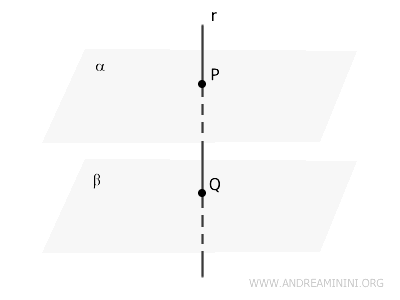
esempio di retta perpendicolare al piano

Questo significa che $ r $ forma un angolo retto con ogni retta contenuta in $ \alpha $ che passa per $ P $ e con ogni retta contenuta in $ \beta $ che passa per $ Q $.

A questo punto, traccio una retta $ s $ appartenente a $ \alpha $, passante per $ P $, e una retta $ t $ appartenente a $ \beta $, passante per $ Q $.

dimostrazione

Poiché $ r $ è perpendicolare a $ \alpha $, $ r $ è perpendicolare a $ s $.

Analogamente, $ r $ è perpendicolare a $ t $.

Ora per ipotesi assurda ipotizzo che $ \alpha $ e $ \beta $ non sono paralleli.

Se i piani $ \alpha $ e $ \beta $ non fossero paralleli, si intersecherebbero lungo una retta $ u $. Quindi, la retta $ u $ apparterrebbe sia a $ \alpha $ che a $ \beta $.

Poiché $ r $ è perpendicolare a tutte le rette di $ \alpha $ passanti per $ P $, $ r $ sarebbe perpendicolare anche alla retta $ u $ dato che $ u $ appartiene al piano $ \alpha $

$$ u \subset \alpha $$

Analogamente, poiché $ r $ è perpendicolare a tutte le rette di $ \beta $ passanti per $ Q $, $ r $ sarebbe perpendicolare anche alla retta $ u $ dato che $ u $ appartiene anche al piano $ \beta $

$$ u \subset \beta $$

Tuttavia, una retta $ r $ non può essere perpendicolare a una stessa retta $ u $ in due punti distinti $ P $ e $ Q $, poiché questo violerebbe l'unicità della perpendicolare in un punto.

Pertanto, la supposizione che $ \alpha $ e $ \beta $ non siano paralleli è falsa.

Di conseguenza, è vero il contrario, ossia i due piani sono paralleli.

Dimostrazione alternativa

Considero una retta $ r $ è perpendicolare al piano $ \alpha $ nel punto $ P $.

Poiché la retta $ r $ è perpendicolare a $ \alpha $ nel punto $ P $, il vettore direttore di $ r $, indicato come $ \vec{v} $, è un vettore normale (ortogonale) al piano $ \alpha $.

Questo implica che $ \vec{v} $ è perpendicolare a ogni vettore contenuto in $ \alpha $.

Allo stesso modo, la retta $ r $ è perpendicolare a $ \beta $ nel punto $ Q $. Quindi, $ \vec{v} $ è normale anche al piano $ \beta $.

Poiché $ \vec{v} $ è normale sia a $ \alpha $ che a $ \beta $, i due piani $ \alpha $ e $ \beta $ condividono la stessa direzione normale, ovvero hanno normali parallele.

Quando due piani hanno direzioni normali parallele, i piani sono paralleli tra loro. Quindi, i piani $ \alpha $ e $ \beta $ sono paralleli.

E così via.