Teorema delle tre rette perpendicolari

Se dal punto $ H $ in cui una retta $ r $ è perpendicolare a un piano $ \alpha $ si traccia una retta $ t $ perpendicolare a un'altra retta $ s $ del piano, allora la retta $ s $ è perpendicolare al piano $ \beta $ formato dalle rette $ r $ e $ t $.

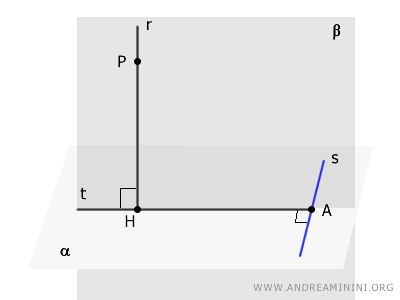
La dimostrazione

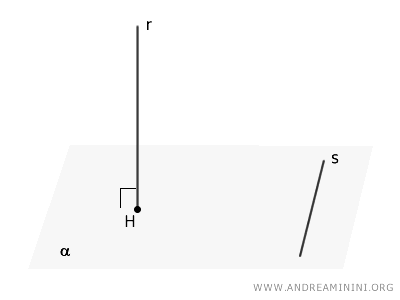
Considero un piano $ \alpha $ e una retta $ r $ perpendicolare al piano ($ r \perp \alpha $) che ha il punto $ H $ come piede della perpendicolare e una retta $ s $ qualsiasi del piano $ \alpha $.

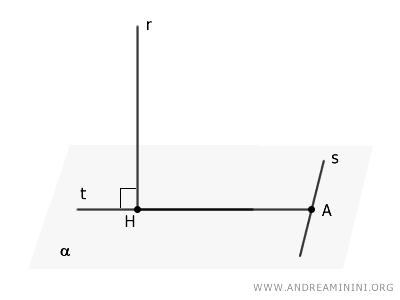
Traccio la retta $ t $ perpendicolare a $ s $ che passa per il punto $ H $ e interseca $ s $ nel punto $ A $.

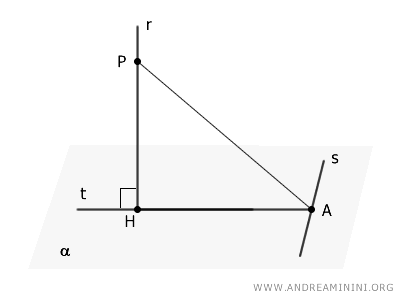
Considero un punto $ P $ qualsiasi della retta $ r $ e traccio il segmento $ PA $.

A questo punto, prendo due punti $ B $ e $ C $ sulla retta $ s $ che siano equidistanti al punto $ A $ e opposti.

In questo modo trovo due segmenti congruenti $ AB \cong AC $.

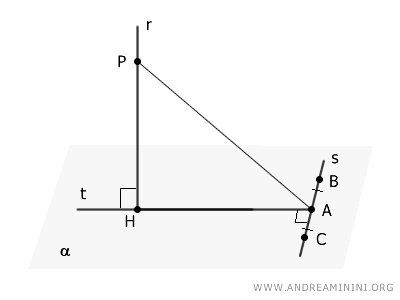
Congiungo i punti $ B $ e $ C $ con il punto $ H $.

Poiché $ H $ si trova sull'asse del segmento $ BC $, deduco che il triangolo $ BCH $ è isoscele, quindi ha i lati obliqui congruenti $ BH \cong CH $.

 

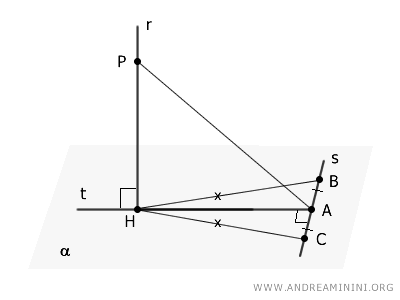
Poi congiungo i punti $ B $ e $ C $ con il punto $ P $ sulla retta $ r $.

I triangoli BPH e CPH sono congruenti perché hanno un lato coincidente $ HP $, un lato congruente $ BH \cong CH $ e l'angolo tra questi congruente (90°). Quindi, i segmenti $ BP \cong CP $ sono congruenti.

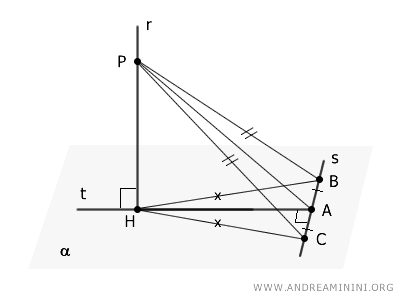
Da questo deduco che il triangolo $ BCP $ è un triangolo isoscele, perché ha i lati congruenti $ BP \cong CP $.

Quindi, il segmento $ AP $ è sia la mediana che l'asse e l'altezza del triangolo. Questo vuol dire che il segmento $ AP $ è perpendicolare alla base $ BC $ del triangolo $ BCP $

$$ AP \perp s $$

In conclusione, sapendo che $ s $ è perpendicolare sia a $ AH $ che a $ AP $, posso dedurre che $ s $ è perpendicolare anche al piano $ \beta $ formato dai due segmenti $ AH $ e $ AP $ ossia dal piano formato dalle rette $ r $ e $ t $.

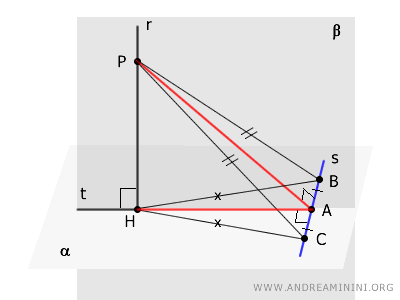
E così via.