Il teorema delle rette perpendicolari al piano

Se due rette \( r \) e \( s \) sono perpendicolari allo stesso piano \( \alpha \) allora le due rette sono parallele tra loro $ r \parallel s $.

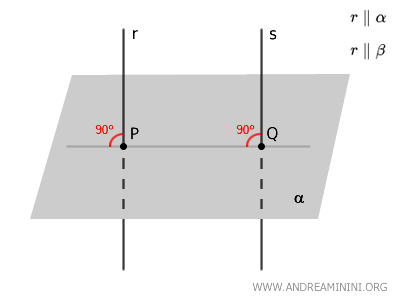
La dimostrazione

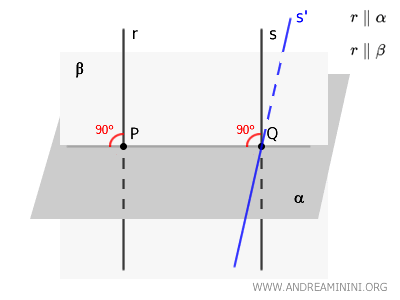
Considero due rette \( r \) e \( s \) perpendicolari al piano \( \alpha \).

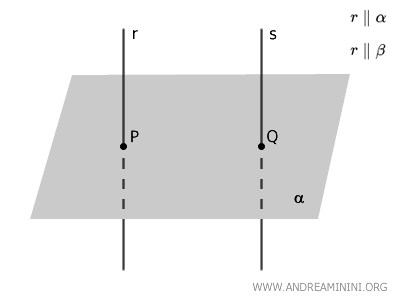
I punti P e Q sono i piedi delle perpendicolari sul piano \( \alpha \).

$$ r \perp \alpha $$

$$ s \perp \alpha $$

Per la definizione di perpendicolarità, ogni retta perpendicolare al piano forma un angolo retto (\(90^\circ\)) con tutte le rette contenute sul piano stesso \( \alpha \).

Quindi, le rette \( r \) e \( s \) formano un angolo retto anche con la retta $ PQ $ che risiede sul piano \( \alpha \) perché passa per i punti $ P $ e $ Q $ ovvero per i piedi delle perpendicolari.

Ora utilizzo la retta \( r \) e la retta \( PQ \) per definire un secondo piano \( \beta \).

Le rette \( r \) e \( PQ \) sono complanari nel piano \( \beta \) per costruzione.

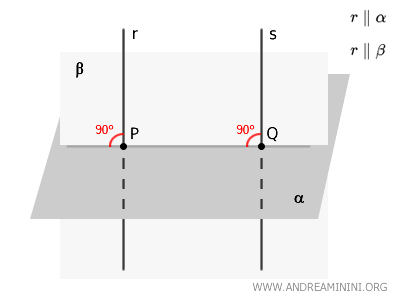
Ora, ammettiamo per assurdo che le rette \( r \) e \( s \) non siano parallele tra loro e vediamo che succede

Non essendo parallele, allora deve esistere un punto di intersezione tra di esse oppure esiste un angolo diverso da \(90^\circ\) tra le due rette.

Tuttavia, in entrambi i casi questo porta a una contraddizione

• Se le rette $ r $ e $ s $ sono incidenti sul piano $ \beta $, allora almeno una delle due ha un angolo diverso da \(90^\circ\) rispetto alla retta $ PQ $ e questo contraddice il fatto che $ r $ e $ s $ sono perpendicolari con tutte le rette del piano, tra le quali c'è anche la retta $ PQ $
  
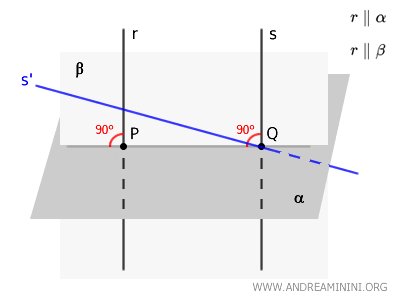
• Se le rette $ r $ e $ s $ non sono incidenti sul piano $ \beta $ e non sono parallele, sono sghembe, allora almeno una delle due ha un angolo diverso da \( 90° \) rispetto al piano $ \alpha $ e questo contraddice l'ipotesi iniziale.
  

Quindi l'ipotesi che \( r \) e \( s \) non siano parallele tra loro è falsa, perché porta a una contraddizione.

Pertanto, \( r \) e \( s \) non possono che essere parallele tra loro.

Note a margine

Alcune osservazioni e note a margine sul teorema.

• Teorema delle rette perpendicolari a un'altra retta nello spazio
  Nello spazio tridimensionale (3D), il teorema secondo cui due rette perpendicolari alla stessa retta sono parallele tra loro non è valido. Questo principio vale solo nel piano bidimensionale (2D), dove la geometria è più restrittiva.
  
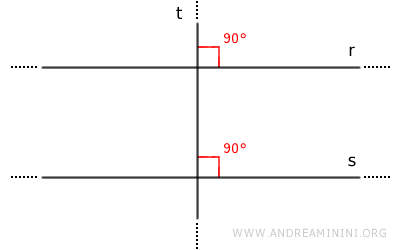
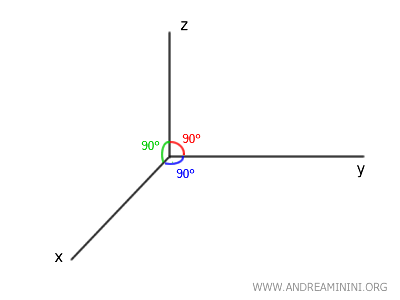
  Perché questo teorema valido sul piano, non vale anche nello spazio 3D? Nel piano (2D), due rette che sono perpendicolari alla stessa retta devono essere parallele perché nel piano non esiste un'altra direzione in cui le due rette possano "deviare". In altre parole, la perpendicolarità a una stessa retta implica che le due rette giacciono su rette parallele. Nello spazio tridimensionale, però, le due rette perpendicolari a una stessa retta possono appartenere a piani diversi e, di conseguenza, non essere parallele. Questo accade perché lo spazio 3D offre una libertà maggiore rispetto al piano: una retta può essere inclinata in molteplici direzioni pur rimanendo perpendicolare alla stessa retta.

  Esempio. Nel sistema cartesiano tridimensionale gli assi cartesiani (\(x\)-\(y\)-\(z\)) sono perpendicolari fra loro ossia formano un angolo di 90°:
  - La retta \(x\) è perpendicolare sia alla retta \(y\) che alla retta \(z\).
  - La retta \(y\) è perpendicolare sia alla retta \(x\) che alla retta \(z\).
  - La retta \(z\) è perpendicolare sia alla retta \(x\) che alla retta \(y\).
  Tuttavia, nessuna coppia di queste rette (\(x, y, z\)) è parallela, perché ciascuna appartiene a un piano diverso (\(xy\), \(xz\), \(yz\)).
  

E così via.