Come rappresentare un insieme con le stringhe
Ci sono diversi modi per rappresentare un insieme in un programma informatico del computer. Uno dei metodi più usati sono le stringhe.
Cosa sono le stringhe? Sono sequenze di 0 e 1 ( bit ) che identificano l'appartenenza o meno di un elemento ai all'insieme A.
Un esempio pratico
Definisco l'insieme universo U che conterrà tutti gli insiemi dell'area di lavoro.
L'insieme U è composto da 10 elementi.
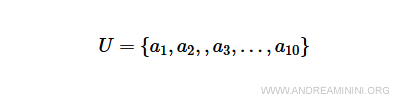
Nota. La cardinalità dell'insieme universo n=|U| deve essere sufficiente per contenere tutti gli elementi degli insiemi che dovrò definire. Inoltre, il numero n di elementi deve anche essere inferiore alla memoria del computer. Per questo motivo, nella rappresentazione al computer l'insieme universo U è comunque un insieme finito e limitato. Non può essere un insieme infinito.
Una volta definito l'insieme universo, posso definire tutti gli altri insiemi che mi servono.
Definisco l'insieme A.
L'insieme A è composto dagli elementi a2, a4, a6.
Per rappresentarlo inserisco 1 nelle posizioni dell'indice i=2,4,6 lasciando a zero le altre.
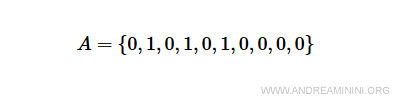
Spiegazione. La prima posizione indica a1=1, la quarta posizione indica a4=1, al sesta posizione indica a6=1. Tutte le altre k posizioni indicano ak=0.
Definisco l'insieme B
Per fare un altro esempio, definisco un insieme B composto dagli elementi a1, a4.
Uso la stessa tecnica per rappresentarlo.
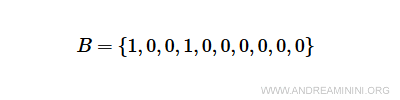
Sono due esempi di rappresentazione dell'insieme tramite le stringhe di bit.
A cosa serve la rappresentazione tramite le stringhe? La rappresentazione degli insiemi tramite le stringhe di bit mi permette di svolgere tutte le operazioni tra gli insiemi scorrendo gli elementi che hanno la stessa posizione (indice).
Unione
L'unione tra A e B la ottengo inserendo 1 se almeno un elemento i-esimo di A o di B è uguale a 1.
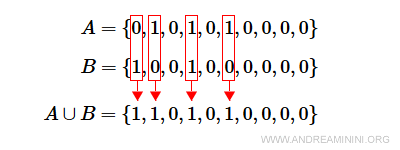
Si ottiene con l'operatore logico OR ( disgiunzione ).
Nota. L'unione A∪B è uguale al sottoinsieme {1,2,4,6}.
Intersezione
L'intersezione A⋂B si realizza scrivendo 1 nell'elemento i-esimo se entrambi gli elementi i-esimi di A e B sono uguali a 1.
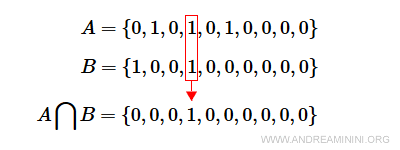
Si ottiene con l'operatore l'ogico AND ( congiunzione ).
Nota. L'intersezione A⋂B è uguale al sottoinsieme {4}.
Differenza A-B
La differenza A-B si ottiene mettendo a zero gli elementi i-esimi uguali a 1 sia nell'insieme A e sia nell'insieme B.
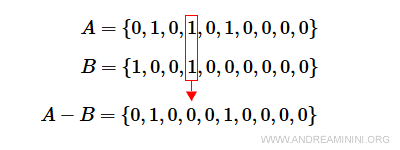
Nota. L'insieme differenza A-B è composto dagli elementi { 2, 6}. E' eliminato l'elemento a4 perché è contenuto sia in A che in B.
Insieme complementare
Per calcolare il complementare dell'insieme A sostituisco ogni elemento 1 con 0 e viceversa.
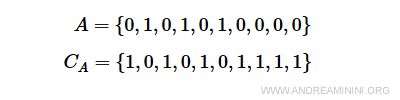
L'insieme complementare si ottiene facilmente usando l'operatore logico NOT ( negazione ).
Sottoinsiemi
Riprendo l'insieme A={2,4,6}
Per rappresentare il sottoinsieme S⊆A con S={2,6} scrivo.
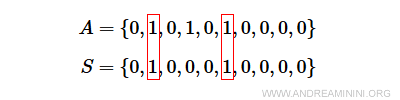
Nota. La stringa S ha i bit uguali a 1 soltanto nelle posizioni dell'indice i=2 e i=6.
Insieme vuoto
Per rappresentare l'insieme vuoto metto a zero tutte le posizioni i-esime della stringa.
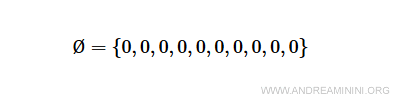
E così via.
