La forma trigonometrica dei numeri complessi

Un numero complesso z=a+bi può essere rappresentato anche in forma trigonometrica $$ z = r \cdot [\cos(\alpha)+i \cdot \sin(\alpha)] $$

Dove r è il modulo e l'angolo α è l'argomento delle coordinate polari del numero complesso z=a+bi sul piano.

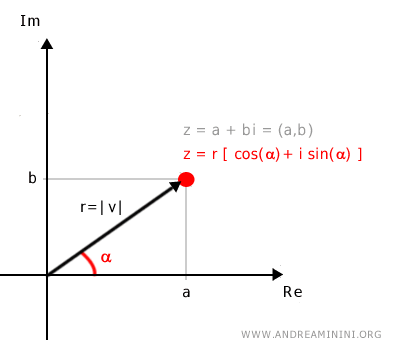
Per questa ragione la forma trigonometrica di z=a+bi è anche detta forma polare del numero complesso.

A cosa serve la forma trigonometrica dei numeri complessi? La forma trigonometrica dei numeri complessi rende più semplici le operazioni di moltiplicazione, divisione, potenza e radice n-esima dei numeri complessi.

Un esempio pratico

Considero il numero complesso

$$ z=3+2i $$

Il numero complesso corrisponde al punto P alle coordinate cartesiane (x,y)=(3,2) sul piano di Gauss.

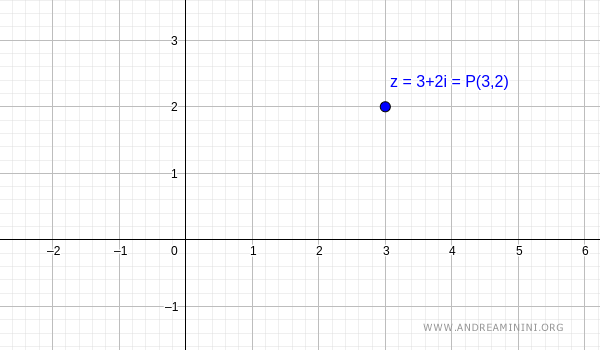
Lo stesso numero complesso corrisponde al vettore v che congiunge l'origine O (polo) e il punto P:(3,2).

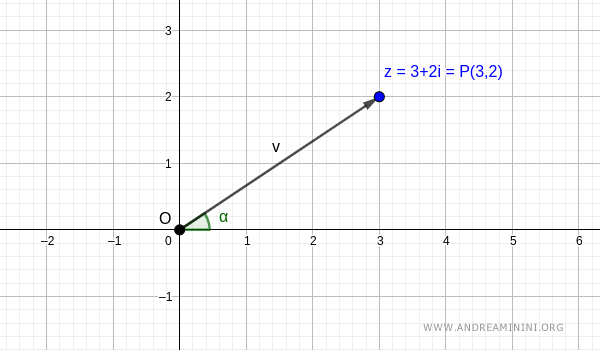
Nota. Il vettore ha una lunghezza (modulo) pari a |v| e un angolo (argomento) pari ad alfa. Per il momento non li conosco ancora ma posso calcolarli facilmente tramite le coordinate polari del punto P.

Costruisco una circonferenza con centro O e raggio r=|v| che passa per il punto P(3,2).

Le proiezioni del punto P sugli assi sono le componenti (x,y)=(3,2) del numero complesso z=3+2i con x=3 e y=2.

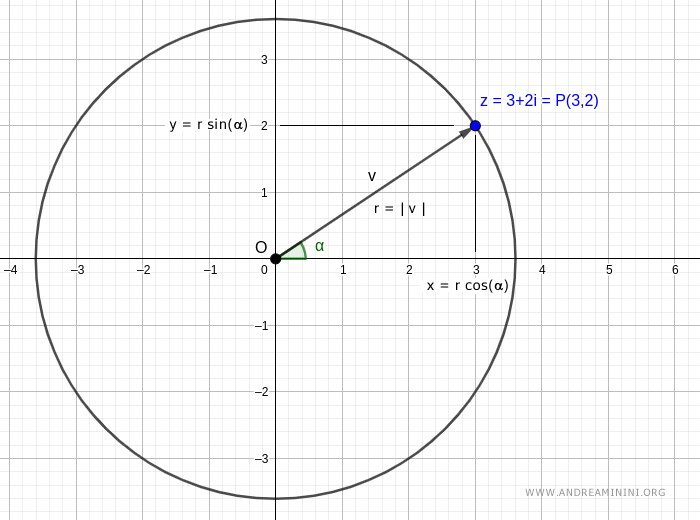
Sapendo che in trigonometria il punto x = r·cos(α) è il coseno dell'angolo alfa moltiplicato per il raggio della circonferenza (r)

$$ z=x+yi= 3+2i $$

$$ z=(r \cdot \cos \alpha)+yi= 3+2i $$

Il punto y = r·sin(α) è invece il seno dell'angolo alfa moltiplicato per il raggio della circonferenza (r).

$$ z= (r \cdot \cos \alpha)+(r \cdot \sin \alpha) \cdot i= 3+2i $$

Metto in evidenza r e ottengo la forma trigonometrica del numero complesso.

$$ z=r \cdot [ \cos \alpha)+ i \cdot \sin \alpha]= 3+2i $$

La lunghezza del raggio (r) e l'ampiezza dell'angolo alfa (α) sono le coordinate polari del punto P:(3,2) sul piano, ossia il modulo e l'argomento del vettore v.

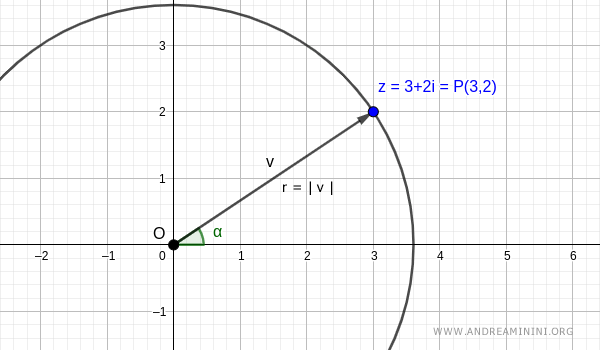
Il raggio r = |v| è detto modulo del numero complesso.

Posso calcolarlo usando il teorema di Pitagora con le coordinate cartesiane (x,y)=(3,2) del punto P

$$ d = \sqrt{x^2+y^2}=\sqrt{3^2+2^2} = \sqrt{13} = 3.61 $$

L'angolo alfa (α) è detto argomento del numero complesso.

Per calcolarlo uso la seconda relazione fondamentale della trigonometria.

$$ \alpha = \arctan \frac{y}{x} = \arctan \frac{2}{3} = 33.69° $$

Spiegazione. In base alla seconda relazione fondamentale della trigonometria $$ \tan \alpha = \frac{\sin \alpha}{\cos \alpha} $$ Sapendo che x=d*cos(alfa) e y=d*sin(alfa) $$ \tan \alpha = \frac{ \frac{y}{d} }{ \frac{x}{d} } $$ $$ \tan \alpha = \frac{y}{d} \cdot \frac{d}{x} $$ $$ \tan \alpha = \frac{y}{x} $$ Calcolo l'arcotangente a entrambi i membri dell'equazione per ottenere l'angolo alfa. $$ \arctan( \tan \alpha) = \arctan( \frac{y}{x} ) $$ $$ \alpha = \arctan( \frac{y}{x} ) $$

Ho ottenuto le coordinate polari del punto P

$$ P:[r \ ; \ \alpha] = [ \sqrt{13} , 33.69° ] $$

che corrispondono il modulo (r) e l'argomento (α) del numero complesso in forma trigonometrica.

$$ z=d \cdot [ \cos \alpha)+ i \cdot \sin \alpha]= 3+2i $$

$$ z=\sqrt{13} \cdot [ \cos 33.69°)+ i \cdot \sin 33.69°]= 3+2i $$

Dal punto di vista grafico

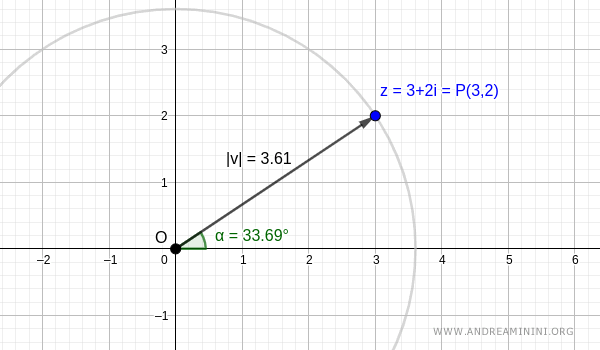
La dimostrazione

Tra i numeri complessi e i punti del piano c'è una corrispondenza biunivoca.

Per ogni numero complesso z=a+bi c'è uno e un solo punto nel piano alle coordinate cartesiane (a,b). E viceversa.

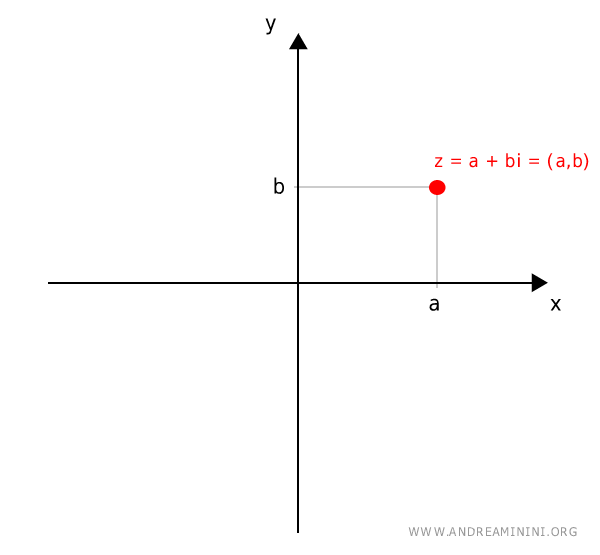
Il punto alle coordinate cartesiane (a,b) posso rappresentarlo usando le coordinate polari [r,α]

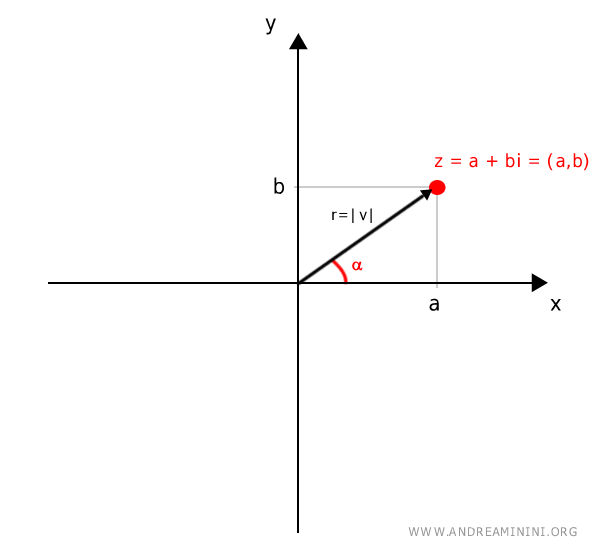
Le coordinate polari sono una coppia formata da due elementi

• Il modulo (r)
  L'elemento r è il modulo del numero complesso, ossia la lunghezza del vettore |v| che congiunge il polo (origine del piano) con il punto P.
• L'argomento (α)
  L'elemento alfa (α) è l'argomento del numero complesso, ossia l'ampiezza dell'angolo che il vettore v forma rispetto al semiasse polare positivo.

Traccio una circonferenza di raggio r=|v| e centro O che passa per il punto (a,b).

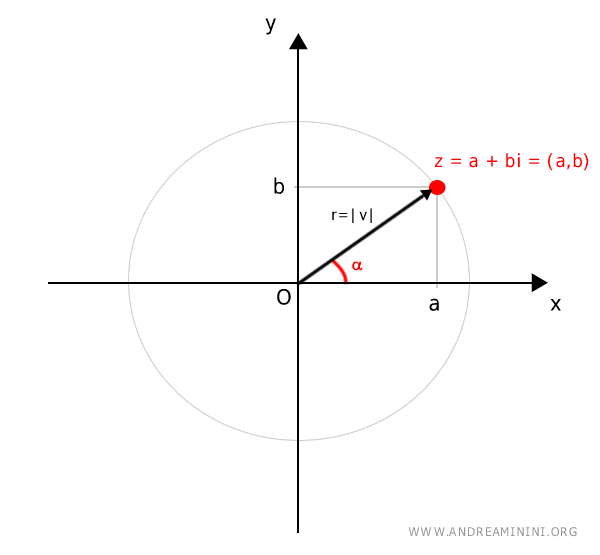
Le proiezioni del punto (a,b) sugli assi cartesiani sono le componenti a,b del numero complesso z=a+bi

$$ z=a+bi $$

In trigonometria i punti a e b sono rispettivamente il coseno e il seno dell'angolo alfa (α) moltiplicati per il raggio della circonferenza (r).

$$ a= r \cdot \cos \alpha $$

$$ b= r \cdot \sin \alpha $$

Dal punto di vista grafico

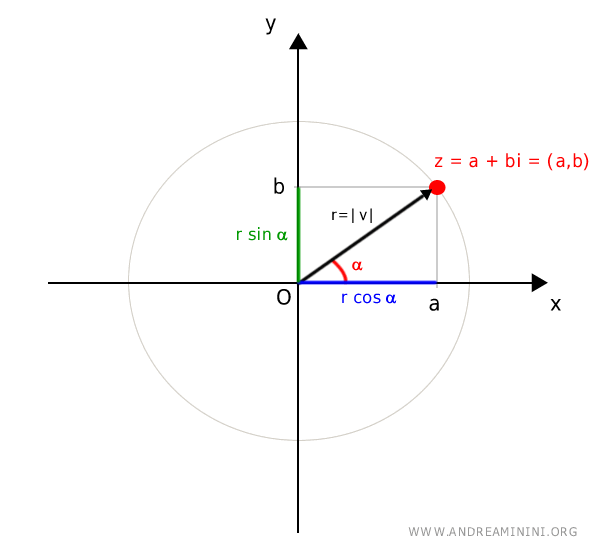
Sostituisco a=r·cos(α) e b=r·sin(α) nel numero complesso z

$$ z=a+bi $$

$$ z=(r \cdot \cos \alpha)+(r \cdot \sin \alpha) \cdot i $$

Metto in evidenza il modulo (r)

Il risultato finale è la forma trigonometrica del numero complesso z=a+bi.

$$ z=r \cdot [ \cos( \alpha)+ i \cdot \sin ( \alpha )] $$

Il modulo (r) del numero complesso lo calcolo tramite il teorema di Pitagora

$$ r = \sqrt{a^2+b^2} $$

L'argomento α del numero complesso lo ottengo tramite l'arcotangente del rapporto b/a

$$ \alpha = \arctan{\frac{b}{a}} $$

Nota. In base alla seconda relazione fondamentale della trigonometria il rapporto tra seno e coseno di un angolo è uguale alla tangente dello stesso angolo. $$ \tan \alpha = \frac{\sin \alpha}{\cos \alpha} $$ Sapendo dalla trigonometria che a=r·cos(α) e b=r·sin(α) allora cos(α)=a/r e sin(α)=b/r. $$ \tan \alpha = \frac{ \frac{b}{r} }{ \frac{a}{r} } $$ $$ \tan \alpha = \frac{b}{r} \cdot \frac{r}{a} $$ $$ \tan \alpha = \frac{b}{a} $$ Applico l'arcotangente a entrambi i membri dell'equazione per calcolare l'angolo alfa (α). $$ \arctan( \tan \alpha) = \arctan( \frac{b}{a} ) $$ $$ \alpha = \arctan( \frac{b}{a} ) $$ Il risultato è l'argomento ossia l'angolo α del numero complesso.

In alternativa, l'argomento α del numero complesso posso calcolarlo anche tramite l'arcocoseno del rapporto a/r

$$ \alpha = \arccos{\frac{a}{r}} $$

Poiché r=√a²+b²

$$ \alpha = \arccos{\frac{a}{\sqrt{a^2+b^2}}} $$

Nota. Sapendo che $$ a = r \cdot \cos \alpha $$ allora il coseno dell'angolo alfa (α) è uguale al rapporto a/r $$ \cos \alpha = \frac{a}{r} $$ Per ottenere l'angolo alfa applico l'arcocoseno a entrambi i membri. $$ \arccos( \cos \alpha ) = \arccos( \frac{a}{r} ) $$ $$ \alpha = \arccos( \frac{a}{r} ) $$

oppure tramite l'arcoseno del rapporto b/r

$$ \alpha = \arcsin{\frac{b}{r}} $$

Poiché r=√a²+b²

$$ \alpha = \arcsin{\frac{b}{\sqrt{a^2+b^2}}} $$

Nota. Sapendo che $$ b = r \cdot \sin\alpha $$ allora il seno dell'angolo alfa (α) è uguale al rapporto b/r $$ \sin \alpha = \frac{b}{r} $$ Per ottenere l'angolo alfa applico l'arcoseno a entrambi i membri. $$ \arcsin( \sin \alpha ) = \arcsin( \frac{b}{r} ) $$ $$ \alpha = \arcsin( \frac{b}{r} ) $$

Le operazioni tra i numeri complessi in forma trigonometrica

Dati due numeri complessi in forma trigonometrica

$$ z_1 = r_1 \cdot ( \cos \alpha + i \cdot \sin \alpha ) $$

$$ z_2 = r_2 \cdot ( \cos \beta + i \cdot \sin \beta ) $$

si può calcolare più agevolmente

• La moltiplicazione
  Il prodotto di due numeri complessi in forma trigonometrica è un numero complesso che ha per modulo il prodotto dei moduli r₁·r₂ e per argomento la somma degli argomenti α+β. $$ z_1 \cdot z_2 = r_1 r_2 \cdot [ \cos ( \alpha+\beta ) + i \cdot \sin ( \alpha+\beta ) ] $$
• La divisione
  Il quoziente di due numeri complessi in forma trigonometrica è un numero complesso che ha per modulo il quoziente dei moduli r₁/r₂ e per argomento la differenza degli argomenti α-β. $$ \frac{z_1}{z_2} = \frac{r_1}{r_2} \cdot [ \cos ( \alpha-\beta ) + i \cdot \sin ( \alpha-\beta ) ] $$
• Il reciproco
  Il reciproco di un numero complesso z=r(cos α +i sin α) in forma trigonometrica è $$ \frac{1}{z_1} = \frac{1}{r_1} \cdot (\cos \alpha - i \cdot \sin \alpha) $$
• La potenza
  La potenza n-esima di un numero complesso in forma trigonometrica è un numero complesso che ha per modulo la potenza n-esima del modulo iniziale r₁ⁿ e per argomento il prodotto tra l'esponente e l'argomento iniziale n·α . $$ z_1^n = r_1^n \cdot [ \cos(n \cdot \alpha) + i \cdot \sin(n \cdot \alpha)] $$

E così via.