Il piano di Gauss
Il piano di Gauss (o piano complesso) è un sistema di assi cartesiani Oxy usato per rappresentare i numeri complessi. L'asse x è detto asse reale (Re) mentre l'asse y è detto asse immaginario (Im).
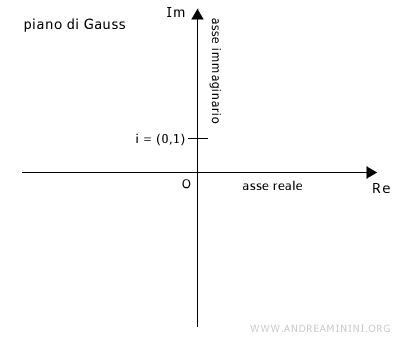
Il simbolo i è l'unità immaginaria alle coordinate (0,1).
Ogni numero complesso è una coppia ordinata (a,b) di numeri reali.
$$ z=(a,b) $$
Pertanto, c'è una corrispondenza biunivoca tra i numeri complessi e i punti del piano cartesiano (x,y).
Ogni numero complesso è un punto del piano e viceversa.
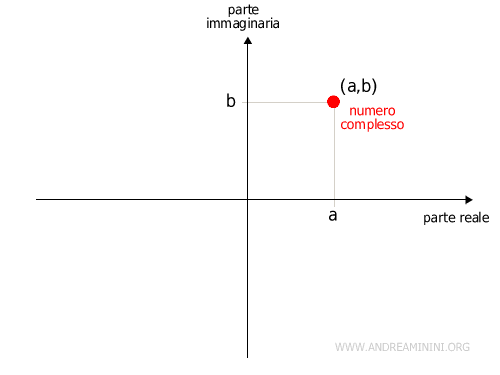
In questo caso sull'asse delle ascisse misuro i numeri reali mentre sulle ordinate i numeri immaginari.
Questo mi permette di usare il piano cartesiano per rappresentare geometricamente i numeri complessi, perché ogni punto del piano è composto da una parte reale e una parte immaginaria.
Questo tipo di diagramma è detto piano complesso o piano di Gauss.
Sapendo che esiste una corrispondenza biunivoca tra i punti del piano e i vettori, si può anche affermare che ogni numero complesso è un vettore v con componenti (a,b). E viceversa.
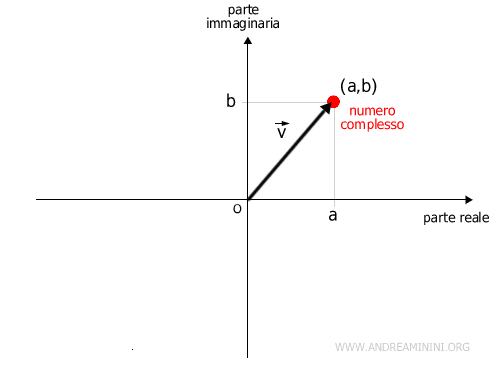
In altre parole, ogni numero complesso $ a+bi $ è associato a uno e un solo vettore $ \vec{v} $ in $ \mathbb{R^2} $ e viceversa.
$$ a + bi \Longleftrightarrow \vec{v} = \begin{pmatrix} a \\ b \end{pmatrix} $$
Quest'ultima considerazione è alla base della rappresentazione polare dei numeri complessi.
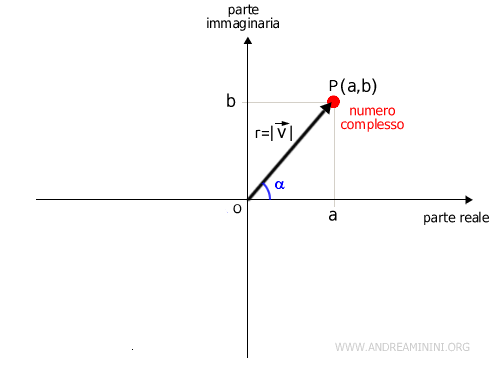
Nel sistema di coordinate polari ogni numero complesso $ z=a+bi $ è associato a una coppia di valori (r;α):
- Il modulo (r) che indica la lunghezza del vettore $ \vec{v} $ tra l'origine O del piano di Gauss (detta "polo") e il punto P(a;b)
- L'argomento (α) che indica l'ampiezza dell'angolo tra il vettore e il semiasse positivo del piano di Gauss (detto asse polare) misurata in senso antiorario.
Nota. Nel sistema di coordinate polari l'origine O del piano di Gauss, ossia il polo, ha le coordinate (0;α) con una qualsiasi ampiezza dell'angolo α. Inoltre, poiché l'ampiezza dell'angolo α è equivalente a infinite ampiezze equivalenti del tipo $ α+2kπ $ che si ottengono sommando k vole l'angolo giro ($ 2π=360° $), si considera come argomento principale soltanto l'ampiezza dell'angolo compresa tra $ 0≤α<2π $
Un esempio pratico
Considero il numero complesso z=2+3i
$$ z=2+3i $$
La parte reale del numero complesso è 2 mentre il coefficiente della parte immaginaria è 3.
Pertanto, il numero complesso corrisponde alle coordinate (2,3) sul piano di Gauss.
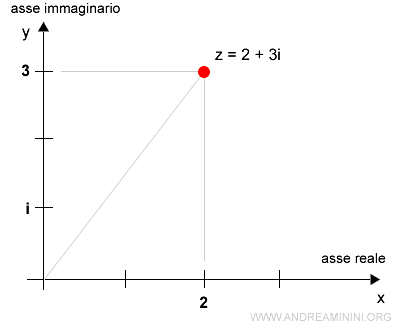
Tra il punto (2,3) e il numero complesso z=2+3i c'è una corrispondenza biunivoca.
Dimostrazione. Il punto (2,3) posso riscriverlo come somma di un numero reale (2,0) e di un numero immaginario (0,3) $$ (2,3) = (2,0)+(0,3) $$ Sapendo che ogni numero immaginario è il prodotto dell'unità immaginaria per un numero reale, posso riscrivere (0,3)=(0,1)·(3,0) $$ (2,3) = (2,0)+[(0,1) \cdot (3,0)] $$ Indico l'unità immaginaria con il simbolo i=(0,1) $$ (2,3) = (2,0)+[i \cdot (3,0)] $$ Sia (2,0) che (3,0) sono numeri reali (2,0)=2 e (3,0)=3. $$ (2,3) = 2+3i $$ Il risultato finale è il numero complesso z=2+3i in forma algebrica.
E così via.
